【Leetcode】873. Length of Longest Fibonacci Subsequence

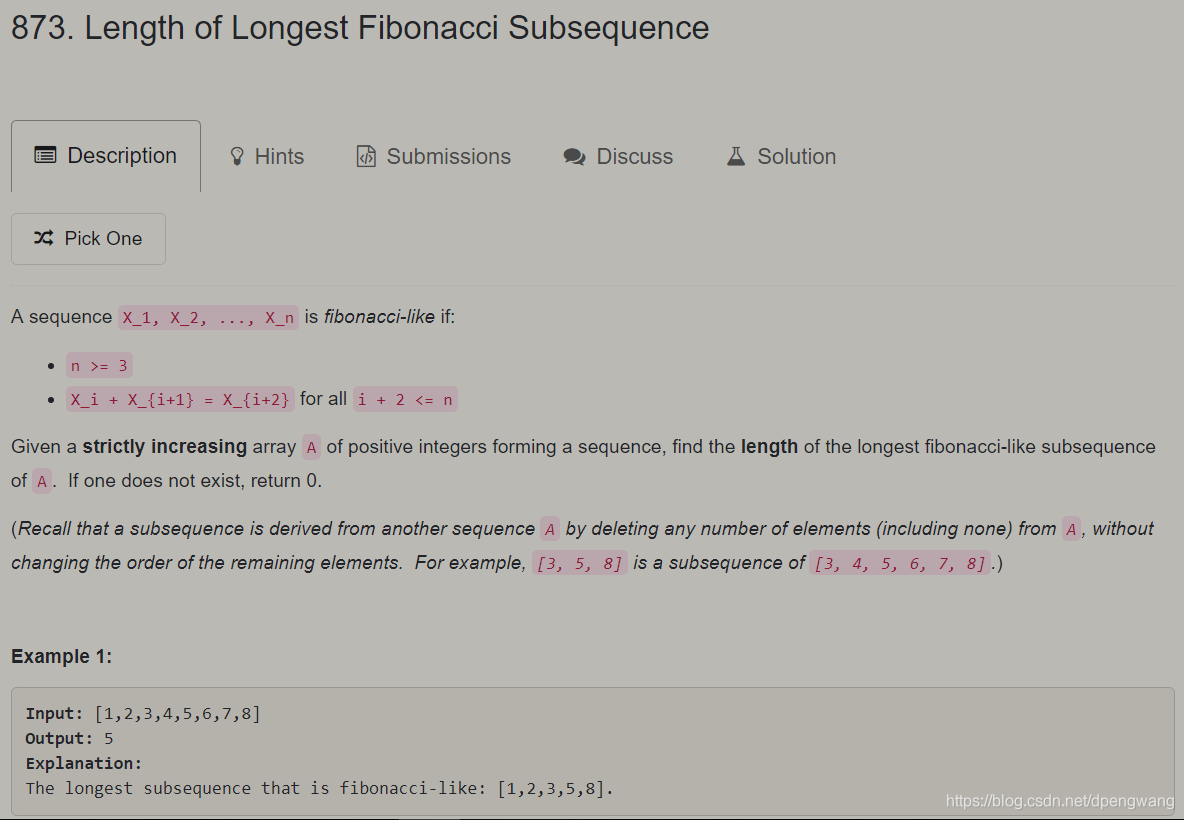
给定一个严格单调递增的数组，求数组中最多有多少个数满足斐波拉契数列，即a[i] = a[i-1]+a[i-2]

方法1

想想怎么确定一个斐波拉契数列。
确定前两个元素就能确定一个斐波拉契数列，所以我们只要遍历数组找到所有的点对，以他们为起始的两个数就能找到数组中所有满足以这两个数为起点的斐波拉契数列中的数。这样做的时间复杂度为$O(n^{2}log(n))$ ~ $O(n^3)$

class Solution:
    def lenLongestFibSubseq(self, A):
        """
        :type A: List[int]
        :rtype: int
        """
        dictionary = {}
        res = 0
        for i in A:
            dictionary[i]=1
        for i in range(len(A)):
            for j in range(i+1,len(A)):
                a = A[i]
                b = A[j]
                count = 0
                while(a+b in dictionary):
                    tmp = b
                    b = a+b
                    a = tmp
                    count +=1
                count = count +2 if count!=0 else 0
                res = max(res,count)
        return res

方法2

用dp的思想来做，用dp[i][j]来表示以index =i和j的两个数为最后两个数的斐波拉契数列，那么我们可以得到以下的递推方程

dp[i][j] = dp[k][i] +1	
k 是A[j] -A[i]对应的index，前提是A[j] -A[i]在数组中存在

因为index和值是一一对应的，所以我们可以用把值当做key，索引当做value来存储数组。
如果abc三个数能构成斐波拉契数列，那么以bc结尾的fb的长度为以ab结尾的fb的长度加一。

class Solution:
    def lenLongestFibSubseq(self, A):
        """
        :type A: List[int]
        :rtype: int
        """
        dictionary = {}
        res = 0
        for index,value in enumerate(A):
            dictionary[value] = index
        dp = [[2]*len(A) for i in range(len(A))]
        for i in range(len(A)):
            for j in range(i+1,len(A)):
                if A[j] -A[i] < A[i] and A[j] - A[i] in dictionary:
                    index = dictionary[A[j] - A[i]]
                    dp[i][j] = dp[index][i] + 1
                    res = max(res,dp[i][j])
        return res

小结

上面两种方法都是用两个元素确定了一条斐波拉契数列。