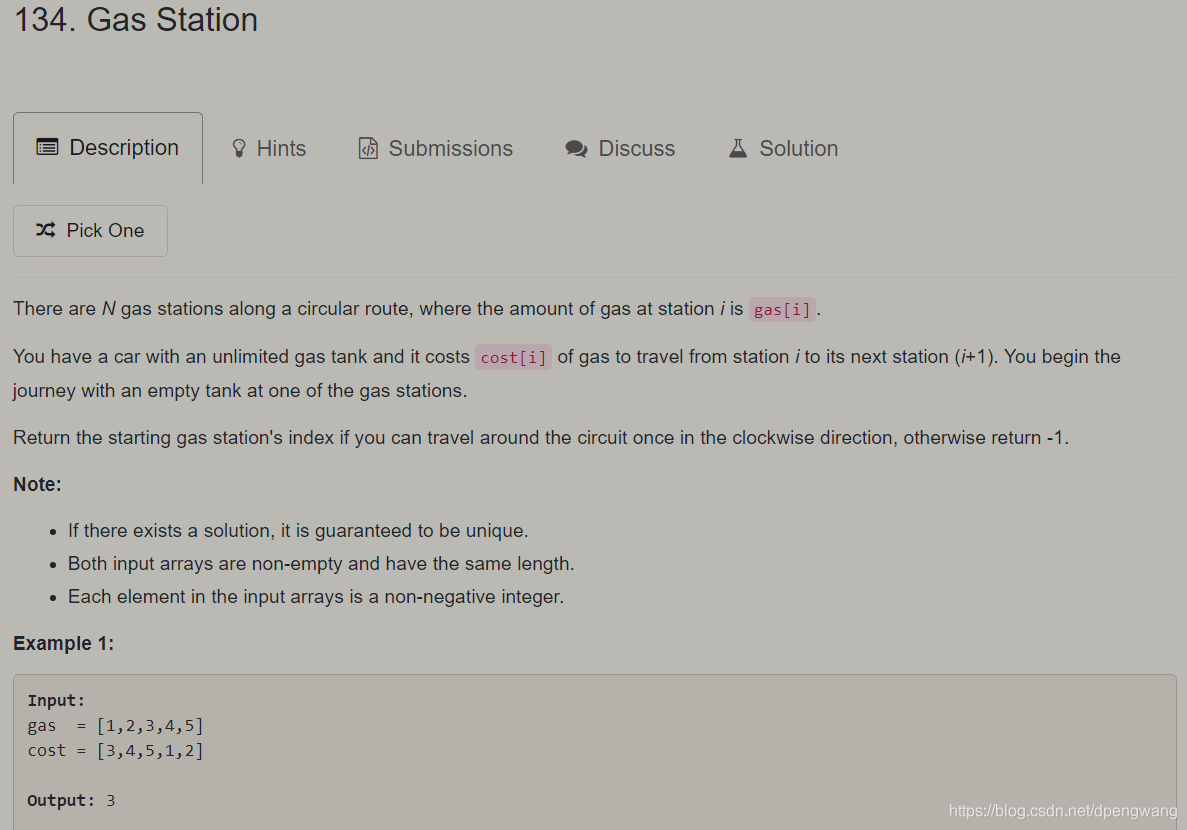
给定两个数组,gas表示在该点能获得多少油(gas首尾相连),cost表示在从该点到下一点要耗费多少油,求从哪一点出发可以重新返回该点
方法1
暴力法,对于每个gas点,尝试从该点出发是否能绕一圈回来,对于某一点,剩余的油量先加油再减去cost,如果大于等于0,表示能到下一个点,如此循环。
时间复杂度为O(n2n^{2}n2),可以AC
class Solution:
def canCompleteCircuit(self, gas, cost):
"""
:type gas: List[int]
:type cost: List[int]
:rtype: int
"""
for i in range(len(gas)):
end = i
start = i
gas_res = gas[start]
while(gas_res - cost[start] >= 0):
gas_res -= cost[start]
start = (start+1)%len(gas)
gas_res += gas[start]
if start == end:
return i
return -1
方法2
这道题可以用线性的时间复杂度的来解决。
首先明确一件事,就是如果gas的总和大于cost的总和,那么一定会存在一个点满足条件。即攒的油总能填补消耗的油,就能回到原点。
我们用remain表示到达某点后油箱里剩的油,如果大于0,说明能到达该点,否则就无法从上个点到达该点 ,我们把起点重新设置为该点。
用debt表示到从index=0的位置到达当前的点所欠的油,如果后面remain的油能后把前面欠的油补上,那说明可从开始攒油的地方出发可以回到原点(用攒下来的油还欠的油,能还的上,就能通过)。
class Solution:
def canCompleteCircuit(self, gas, cost):
"""
:type gas: List[int]
:type cost: List[int]
:rtype: int
"""
debt = 0
remain = 0
start = 0
for i in range(len(gas)):
remain += gas[i] -cost[i]
if remain <0:
start = i+1
#这里是加remain 只加欠的
debt += remain
remain = 0
return start if remain + debt >=0 else -1
这里体现贪心主要是在每次设置新的起点上,只要欠油了(remain<0),那么我们就重新设置新的起点,但是每次只要发生欠油,我们就要欠的数额记录下来,以便和后面攒的油量做比较。
品味一下这道题和最大子数组和的中边界调整相似之处。







 本文探讨了加油站问题,即在给定的gas和cost数组中,寻找一个出发点,使得从该点出发能够绕一圈回到原点。文章详细介绍了两种解决方法:一种是时间复杂度为O(n^2)的暴力解法;另一种是更高效的线性时间复杂度的贪心算法。贪心算法的关键在于,当剩余油量小于0时,重新设置起点,并累计欠油量,以确保最终找到的起点能够完成一圈旅行。
本文探讨了加油站问题,即在给定的gas和cost数组中,寻找一个出发点,使得从该点出发能够绕一圈回到原点。文章详细介绍了两种解决方法:一种是时间复杂度为O(n^2)的暴力解法;另一种是更高效的线性时间复杂度的贪心算法。贪心算法的关键在于,当剩余油量小于0时,重新设置起点,并累计欠油量,以确保最终找到的起点能够完成一圈旅行。
















 826
826

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








