二分搜索 边界判别

while(l<r)
{
	mid=(l+r)/2;
	if(mid>x)  r=mid;
	else l=mid+1;
}

1,如果mid是向下取整，那l=mid+1,避免死循环。
2,如果mid是向上取整，r=mid-1，避免死循环。

例题：

public static void main(String[] args) {
	// TODO Auto-generated method stub
	int a[]= {1,1,1,2,3,3,3,4,4,4};
	System.out.println(finddown(a,4));//找4元素的下限
	System.out.println(findup(a,4));//找4元素的上限
}
public static int finddown(int a[],int index)
{
	int l=0;int r=a.length-1;
	while(l<r)
	{
		int mid=(l+r)>>1;//向下取整
		if(a[mid]>=index)
		{
			r=mid;
		}
		else l=mid+1;
	}
	return l;
}
public static int findup(int a[],int index)
{
	int l=0;int r=a.length-1;
	while(l<r)
	{
		int mid=(l+r+1)>>1;//向上取整，r为mid-1
		if(a[mid]<=index)
		{
			l=mid;
		}
		else {
			r=mid-1;
		}
	}
	return l;
}

力扣1802

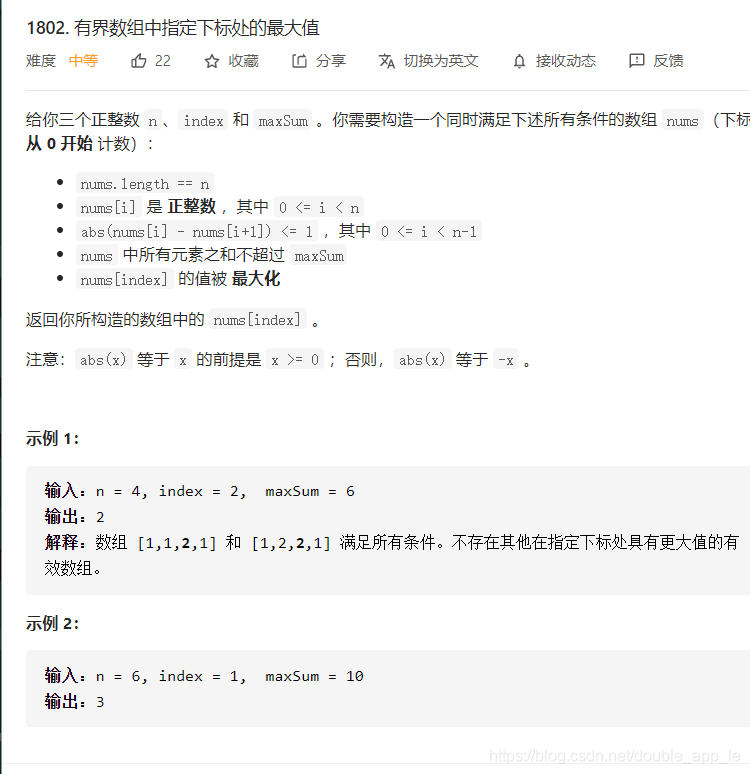
class Solution {
    public int maxValue(int n, int index, int maxSum) {
//
//6/4 1.23232
// 1 1 1 1
//     2
// 1  1    1
//  1  2  3  2 buxing

//10/6=1.232
// 1 1 1 1 1 1
//  1 2 1  
// 2 3 2 1 1  1 
// 3 4 3 //

//14/8=1.12312
//1 1 1 1 1 1 1 1
//              2
//              3
//1 1 1 1 1 2 3 4//14
//1 1 1 1 2 3 4 5 

    // int ans = -1, lo = 1, hi = maxSum;
    //     while (lo <= hi) {
    //         int mid = (lo + hi) >>> 1;
    //         if (check(mid, maxSum, index, n)) {
    //             ans = mid;
    //             lo = mid + 1;
    //         } else {
    //             hi = mid - 1;
    //         }
    //     }
    //     return ans;

   int low=1;int hig=maxSum;

    while(low<=hig)
	{
        int target=(low+hig)/2;//low+1
        if(check(target,maxSum,index,n))//小于等于
        {
            low=target+1;
        }
        else hig=target-1;
    }
    return low-1;
    }
    private boolean check(int target, int sum, int index, int n) {
        long left = target >= index + 1 ? cacl(index + 1, target, -1)
                : (cacl(target, target, -1) + index + 1 - target);
        long right = target >= n - index ? cacl(n - index, target, -1) :
                (cacl(target, target, -1) + n - index - target);
        return left + right - target <= sum;
    }

    private long cacl(int n, int a, int d) {
        return (long) n * a + n * (n - 1) / 2 * d;
    }
}

cf670d2

solution：
二分找ans+判断
log（n=200000000）O(m=10^5)
30O(10^5) 时间复杂度ok了
还需要用快速输入。

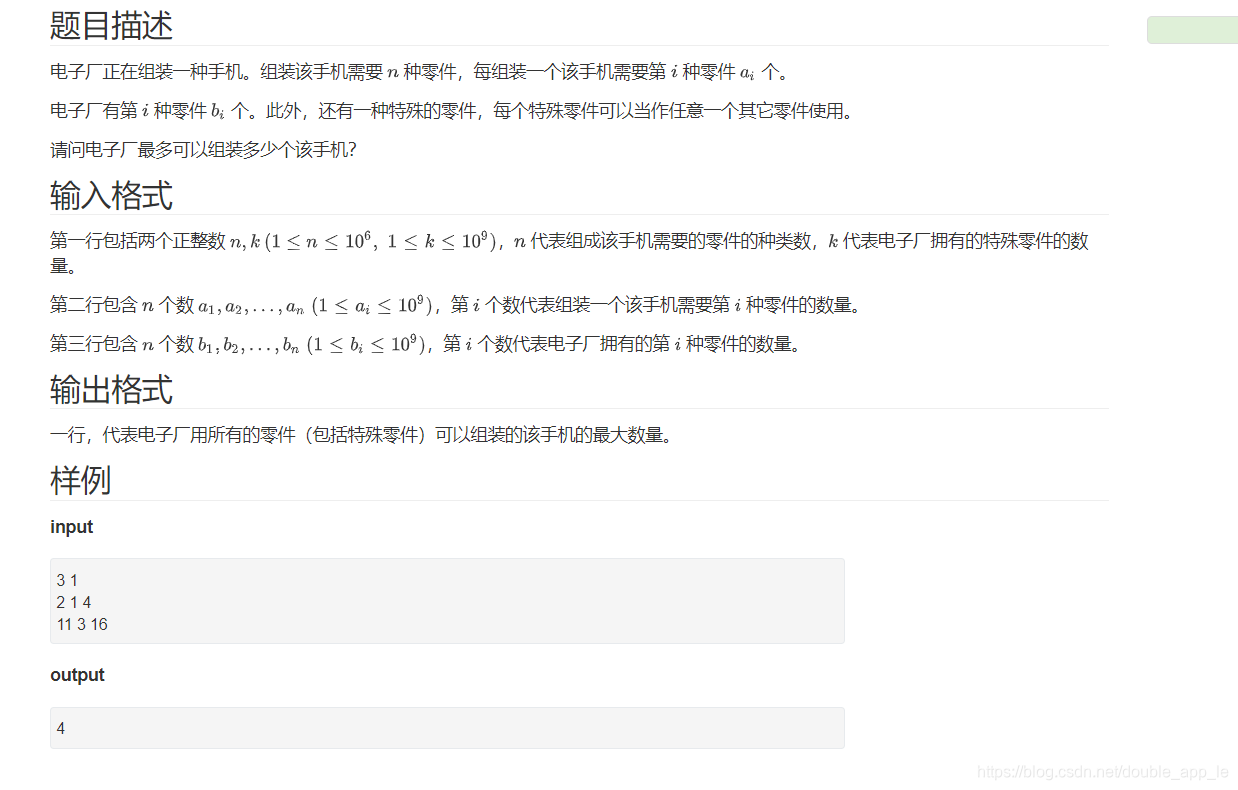
package school;

import java.io.BufferedInputStream;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStream;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.util.Scanner;



public class a6mid {
	static int n;
	static int k;
	static int need[];
	static int sum[];
	public static void main(String[] args) throws IOException {
		// TODO Auto-generated method stub
//		Scanner s=new Scanner(System.in);
		StreamTokenizer st=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
		
		st.nextToken();n=(int)st.nval;
		st.nextToken();k=(int)st.nval;
		need=new int[n];sum=new int[n];
		for(int i=0;i<n;i++)
		{
			st.nextToken();
			need[i]=(int)st.nval;
		}
		for(int j=0;j<n;j++)
		{
			st.nextToken();
			sum[j]=(int)st.nval;
		}
		long lef=0;
		long rig=2000000000;
		while(lef<=rig)
		{
			long mid=(lef+rig)/2;
			if(check(mid))
			{
				lef=mid+1;
			}
			else {
				rig=mid-1;
			}
		}
//		System.out.println(check(1));
		System.out.println(lef-1);
	}
	private static boolean check(long mid) {
		// TODO Auto-generated method stub
		long yu=k;
		for(int i=0;i<n;i++)
		{
			if(sum[i]>(long)mid*need[i]) continue;
			else {
				yu-=(long)((long)mid*need[i]-sum[i]);
				if(yu<0) return false;
			}
		}
		return true;
	}
}