本文详细介绍了十大排序算法，包括冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、计数排序、基数排序和桶排序。分别阐述了每种算法的实现代码、复杂度分析以及稳定性。对于优化和特殊情况，如逆序对和空间复杂度，也进行了探讨。适合初学者深入理解排序算法。
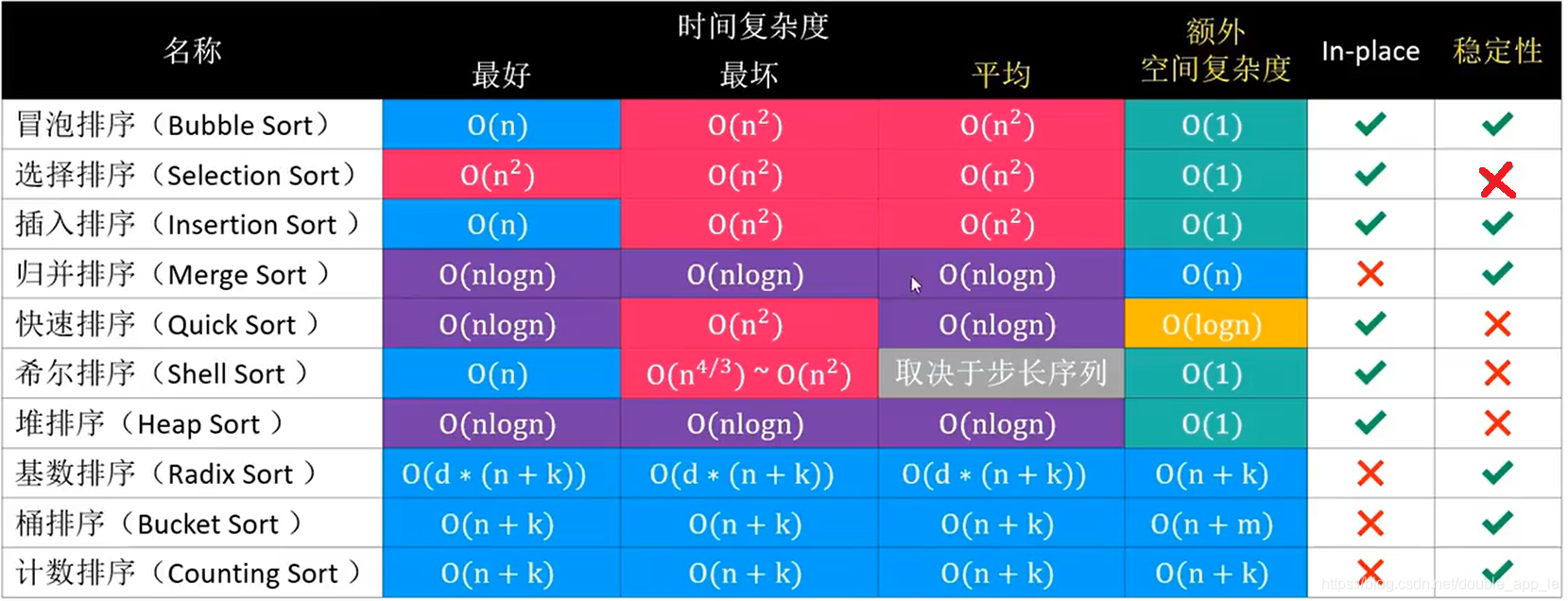
总结
以下表格是基于数组进行排序的一般结论
排序算法的稳定性：
相等的两个元素，排序前后的相对位置不变，则为稳定的算法。
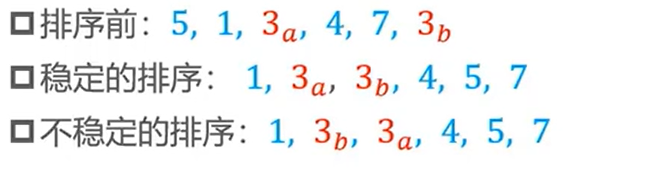
比较类排序
稳定性高：冒泡，插入 ，归并
不稳定：选择，堆排序，快速，希尔
非比较类排序
稳定性高：优化后的计数排序,基数排序,桶排序
原地算法：
不依赖额外的资源，空间复制的为O(1)
分类：
比较排序：
平均最低时间复杂度O（nlogn）
冒泡排序
选择排序
插入排序
希尔排序
归并排序
快速排序
堆排序
非比较排序
计数排序
基数排序
桶排序
冒泡排序(BubbleSort)
实现代码
比较相邻两个元素大小，大的向后移动。形成升序。
int arr[]= {3,23,12,3,4,5};
for(int end=arr.length-1;end>0;end--)
{
for(int begin=1;begin<=end;begin++)
{
if(arr[begin-1]>arr[begin])
{
int t=arr[begin];
arr[begin]=arr[begin-1];
arr[begin-1]=t;
}
}
}
优化1：数组提前完全有序，不需要进行后面操作
int arr[]= {3,23,12,3,4,5};
for(int end=arr.length-1;end>0;end--)
{
boolean sorted=true;
for(int begin=1;begin<=end;begin++)
{
if(arr[begin-1]>arr[begin])
{
int t=arr[begin];
arr[begin]=arr[begin-1];
arr[begin-1]=t;
sorted=false;
}
}
if(sorted) break;
}
优化2：数组尾部有序，减小操作次数，或者已经完全有序，直接结束操作。
int arr[]= {3,23,12,3,4,5};
for(int end=arr.length-1;end>0;end--)
{
int sortedIndex=1;//如果已经完全有序，end直接为1.
for(int begin=1;begin<=end;begin++)
{
if(arr[begin-1]>arr[begin])
{
int t=arr[begin];
arr[begin]=arr[begin-1];
arr[begin-1]=t;
sortedIndex=begin;//记录最后一个无序的下标
}
}
end=sortedIndex;
}
复杂度分析
最坏，平均时间复杂度为：O(n^2)
最好的时间复杂度为：O(n)
空间复杂度：O(1)(因为没有用堆，递归等等）
稳定
选择排序(SelectionSort)
从序列中最大的数，和最末尾的元素交换位置。
实现代码
int arr[]= {3,23,12,3,4,5};
for(int end=arr.length-1;end>0;end--)
{
int maxindex=0;
for(int begin=1;begin<=end;begin++)
{
if(arr[begin]>arr[maxindex])//无论如何都会不稳定
maxindex=begin;
}
int temp=arr[maxindex];
arr[maxindex]=arr[end];
arr[end]=temp;
}
复杂度分析
空间复杂度O(1)
难以优化，时间复杂度O(n^2)。选择最大值的过程交给堆结构，就可以优化，升级成堆排序。
不稳定
插入排序（InsertionSort）
在前面有序元素中，持续插入其他元素。
实现代码
int arr[]= {3,2,4,5,3,6};
for(int begin=1;begin<arr.length;begin++)
{
int begi=begin;
while(begi>0&&arr[begi-1]>arr[begi])//稳定
{
//交换
int temp=arr[begi-1];
arr[begi-1]=arr[begi];
arr[begi]=temp;
begi--;
}
}
代码优化！：
交换操作优化成挪动操作，简化代码
int arr[]= {3,2,4,5,3,6};
for(int begin=1;begin<arr.length;begin++)
{
int begi=begin;
int t=arr[begi];
while(begi>0&&arr[begi-1]>t)
{
//挪动
arr[begi]=arr[begi-1];
begi--;
}
arr[begi]=t;
}
优化代码2 二分搜索优化
用二分搜索插入位置，可以大幅减小比较次数，但是时间复杂度还是O(n^2)
因为后面还是要进行挪动。
public static void main(String[] args) {
// TODO Auto-generated method stub
int arr[]= {2,1,3,5,3,6};
for(int begin=1;begin<arr.length;begin++)
{
int searchindex=search(arr, begin);
int v=arr[begin];
for(int i=begin;i>searchindex;i--)
{
arr[i]=arr[i-1];
}
arr[searchindex]=v;
}
for(int i:arr)
System.out.print(i+" ");
}
public static int search(int arr[],int index)//二分搜索插入位置
{
//在[0,index)找合适的位置插入
int sta=0;
int end=index;
while(sta<end)
{
int mid=(sta+end)/2;
if(arr[index]<arr[mid])
{
end=mid;
}
else
{
sta=mid+1;
}
}
return sta;
}
复杂度分析
逆序对：
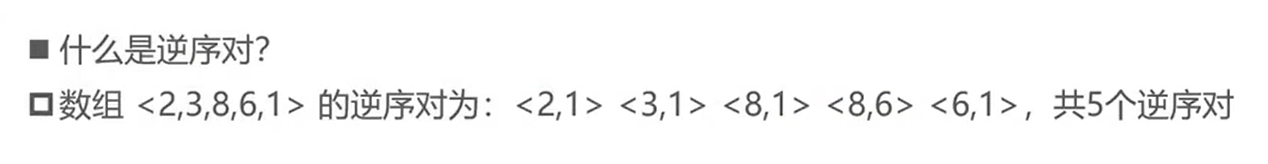
时间复杂度和逆序对数量成正比
最坏，平均时间复杂度为，O(n^2)
最好时间复杂度：O(n)
空间复杂度：O(1)
稳定排序
希尔排序（ShellSort）
根据给出的步长序列，分列用插入排序。
每一次使用完一个步长，逆序对的数量会减少。
如果步长序列为{1,2,4,8}
实现代码
public static void main(String[] args) {
// TODO Auto-generated method stub
int arr[]= {2,1,3,4,3,6,1,1,2,3,4,5,6,7,8,9};
List<Integer> stepSequence=shellStepSequence(arr.length);//根据希尔本人推荐，步长公式，生成步长序列。n/(2^k)
//如果长度是16，对应序列为{1,2,4,8}
// for(int i:stepSequence) System.out.print(i+" ");
for(int step:stepSequence)
{
ShellSort(arr,step);
}
for(int i:arr)
{
System.out.print(i+" ");
}
}
//分成step列
public static void ShellSort(int arr[],int step)
{
for(int col=0;col<step;col++)//col为第几列
{
//每一列的元素对应的下标： col col+step col+step*2 以下用插入排序
for(int begin=col+step;begin<arr.length;begin+=step)
{
int begi=begin;
while(begi>col&&arr[begi-step]>arr[begi])
{
//前一个更大，交换
int temp=arr[begi-step];
arr[begi-step]=arr[begi];
arr[begi]=temp;
begi-=step;
}
}
}
}
public static List<Integer> shellStepSequence(int length)
{
List<Integer> stepSequence=new ArrayList<>();
int step=length;
while((step>>=1)>0)
{
stepSequence.add(step);
}
return stepSequence;
}
复杂度分析
时间复杂度：
最好是O(n)
希尔给出的步长序列，最坏为O(n^2)
已知最好的步长序列（可百度，有相关公式），最坏情狂时间复杂度O(n的4/3）
空间复杂度：就地排序，O(1)
为不稳定排序
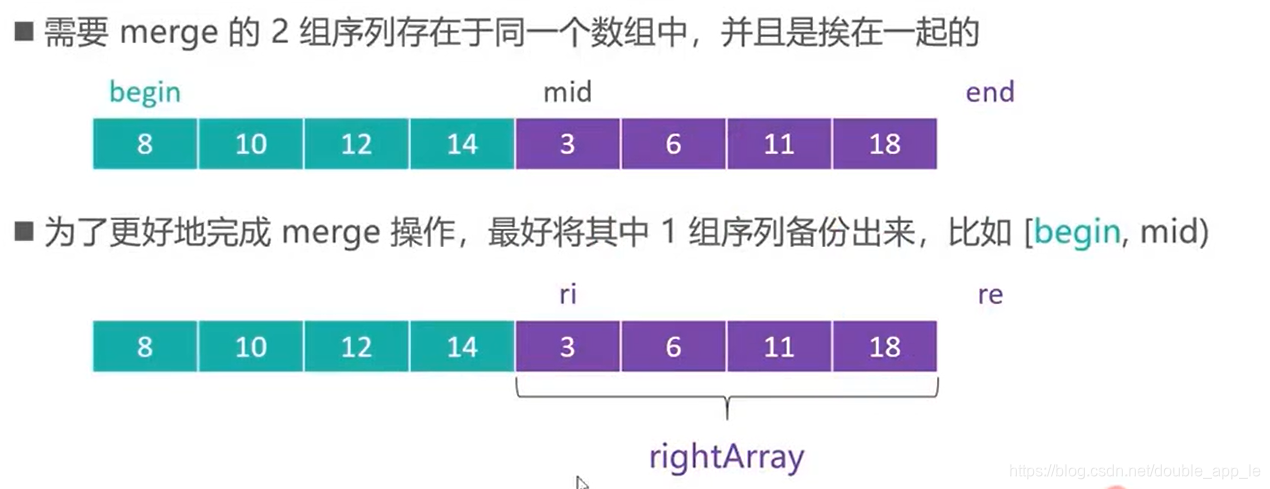
归并排序（MergeSort）
先不断分割，再不断合并
实现代码
public static void main(String[] args) {
// TODO Auto-generated method stub
int arr[]= {2,1,3,4,3,6};
// int arr[]= {3,4,3,6};
sort(arr,0,arr.length);
for(int i:arr)
System.out.print(i+" ");
}
//对[begin,end)进行归并排序
public static void sort(int arr[],int begin,int end)
{
if((end-begin)<2) return;//表示个数小于2
int mid=(begin+end)>>1;
sort(arr,begin,mid);//[begin,mid)
sort(arr,mid,end);//[mid,end)
merge(arr,begin,mid,end);
}
public static void merge(int arr[],int begin,int mid,int end)
{
int li=0;int le=mid-begin;
int ri=mid;int re=end;
int ai=begin;
int leftarr[]=new int[le-li];
for(int i=0;i<le;i++)
{
leftarr[i]=arr[begin+i];
}
while(li<le)//leftarr如果已经遍历完了，就直接退出
{
if(arr[ri]<leftarr[li]&&ri<re)//右边数组的元素更小，插前面,确保稳定性
{
arr[ai++]=arr[ri++];
}
else {
arr[ai++]=leftarr[li++];
}
}
}
复杂度分析
时间复杂度：
有递归
最好最坏平均都是：T(n)=T(n/2)+T(n/2)+O(n)=O(nlogn)
空间复杂度：
O(n/2+logn)=O(n) //logn是对于递归调用的深度（堆使用）
// n/2 创建一个静态全局leftarr
快速排序（QuickSort）
一遍选择第一个作为轴点元素
1，选择轴点元素放中间
2，利用轴点分成小于，大于两边序列
3，在序列中继续把新轴点放中间
本质：将每一个元素转换成轴点元素
实现代码
public static void main(String[] args) {
// TODO Auto-generated method stub
int arr[]= {2,1,3,4,3,6};
quicksort(arr,0,arr.length);
for(int i:arr)
System.out.print(i+" ");
}
public static void quicksort(int arr[],int begin,int end)
{
//范围：[begin,end)
if(end-begin<2) return ;
int pivotinde=pivotindex(arr, begin, end);
//分成 [begin,pivotinde) pivotinde [pivotinde+1,end);
quicksort(arr, begin, pivotinde);
quicksort(arr,pivotinde+1,end);
}
public static int pivotindex(int arr[],int begin,int end)//将序列分两边，轴点在中间，返回轴点下标
{
//范围：[begin,end)
//轴点元素
int pivot=arr[begin];//轴点元素
end--;//最后一个元素
while(begin<end)//begin==end就停止
{
while(begin<end)//找后面比轴点元素小的
{
if(arr[end]>pivot) end--;
else//找到了比轴点元素小或者相等的，放到前面，相等也交换可以，减少栈的使用
{
arr[begin++]=arr[end];break;
}
}
while(begin<end)//找前面比轴点元素大的
{
if(arr[begin]<pivot) begin++;
else//找到了比轴点元素大或者相等的，放到后面，相等也交换可以，减少栈的使用
{
arr[end--]=arr[begin];break;
}
}
}
arr[begin]=pivot;
return begin;
}
复杂度分析
时间复杂度：
最好，平均情况：
轴点左右数量差不多时，
T(n)=2*T(n/2)+O(n)=O(nlogn)
最坏情况：
T(n)=T(n-1)+T(1)+O(n)=O(n^2)
随机选择轴点元素，可以避免最坏情况。
空间复杂度：
递归调用过logn次，所以是O(logn)
随机选择轴点元素优化时间复杂度：
为不稳定排序。
public static int pivotindex(int arr[],int begin,int end)//将序列分两边，轴点在中间，返回轴点下标
{
//范围：[begin,end)
//轴点元素
int pivot=arr[begin];//轴点元素
end--;//最后一个元素
while(begin<end)//begin==end就停止
{
while(begin<end)//找后面比轴点元素小的
{
if(arr[end]>pivot) end--;
else//找到了比轴点元素小或者相等的，放到前面，相等也交换可以，减少栈的使用
{
arr[begin++]=arr[end];break;
}
}
while(begin<end)//找前面比轴点元素大的
{
if(arr[begin]<pivot) begin++;
else//找到了比轴点元素大或者相等的，放到后面，相等也交换可以，减少栈的使用
{
arr[end--]=arr[begin];break;
}
}
}
arr[begin]=pivot;
return begin;
}
堆排序（HeapSort）
对选择排序的一种优化。
实现代码
package 堆排序;
//2021年3月30日下午2:28:55
//writer:apple
public class 堆排序2 {
public static void main(String[] args) {
// TODO Auto-generated method stub
int arr[]= {3,2,4,5,3,6};
Heapsort(arr);
for(int i:arr)
System.out.print(i+" ");
}
public static void adjustheap(int arr[],int i,int size)
{
int temp=arr[i];
for(int k=i*2+1;k<size;k=k*2+1)
{
//大根堆，为升序
// if((k+1)<size&&arr[k+1]>arr[k])
// {
// k++;
// }
// if(arr[k]>temp)
// {
// arr[i]=arr[k];
// i=k;
// }
// else break;
//小根堆，为降序。
if((k+1)<size&&arr[k+1]<arr[k])
{
k++;
}
if(arr[k]<temp)
{
arr[i]=arr[k];
i=k;
}
else break;
}
arr[i]=temp;
}
public static void buildheap(int arr[])
{
for(int i=arr.length/2-1;i>=0;i--)
{
adjustheap(arr, i, arr.length);
}
}
public static void Heapsort(int arr[])
{
buildheap(arr);
for(int i=arr.length-1;i>0;i--)
{
int temp=arr[0];
arr[0]=arr[i];
arr[i]=temp;
adjustheap(arr, 0, i);
}
}
}
复杂度分析
最好最坏，平均时间复杂度：O(nlogn)
空间复杂度为：O(1);
不稳定
计数排序（CountingSort）
1，找出最大值
2，创建maxx空间的counts数组
3，根据出现排序
实现代码
只能对非负整数进行排序
缺点：
int arr[]= {3,2,4,5,3,6,43,23,54,23,12,3};
//找出最大值
int maxx=arr[0];
for(int i=0;i<arr.length;i++)
{
maxx=Math.max(maxx,arr[i]);
}
//创建maxx空间的counts数组
int counts[]=new int[maxx+1];
for(int i=0;i<arr.length;i++)
{
counts[arr[i]]++;
}
int index=0;
//排序
for(int i=0;i<counts.length;i++)
{
while(counts[i]-->0)
{
arr[index++]=i;
}
}
优化代码1
优化后，可以处理负整数
空间优化
排序稳定
步骤：
1，找出最大值 最小值
2，创建maxx-minn+1空间的counts数组
3，counts数组累计次数，用于存放索引
4，/从后往前遍历，可以保持排序稳定性
int arr[]= {3,2,4,5,3,6,43,23,54,23,12,3};
//找出最大值 最小值
int maxx=arr[0];
int minn=arr[0];
for(int i=0;i<arr.length;i++)
{
maxx=Math.max(maxx,arr[i]);
minn=Math.min(minn,arr[i]);
}
//创建maxx-minn+1空间的counts数组
int counts[]=new int[maxx-minn+1];
for(int i=0;i<arr.length;i++)
{
counts[arr[i]-minn]++;
}
//累计次数，用于存放索引
for(int i=1;i<counts.length;i++)
{
counts[i]+=counts[i-1];
}
//从后往前遍历，可以保持排序稳定性
int newarr[]=new int[arr.length];
for(int i=arr.length-1;i>=0;i--)
{
int index=counts[arr[i]-minn]-1;
newarr[index]=arr[i];
counts[arr[i]-minn]--;
}
for(int i=0;i<newarr.length;i++) arr[i]=newarr[i];
复杂度分析
空间复杂度：
数组：
count（整数范围k）
newarr (n)
所以为O(n+k);
时间复杂度：
O(3*n+k) 可以认为是O(n+k)
基数排序（RadixSort）
非常适合整数排序
依次对个位数，十位数，百位数。。进行计数排序
实现代码
public static void main(String[] args) {
// TODO Auto-generated method stub
int arr[]= {3,2,4,5,3,6,43,23,54,23,12,3,1242};
//找出最大值
int maxx=arr[0];
for(int i=0;i<arr.length;i++)
{
maxx=Math.max(maxx,arr[i]);
}
//最大值1242
for(int divider=1;divider<=maxx;divider*=10)//表示除数，用于在countsort中处理余数
{
countsort(arr,divider);
}
for(int i:arr)
System.out.print(i+" ");
}
public static void countsort(int arr[],int divider)
{
//创建10空间的counts数组
int counts[]=new int[10];
for(int i=0;i<arr.length;i++)
{
counts[arr[i]/divider%10]++;
}
//累计次数，用于存放索引
for(int i=1;i<counts.length;i++)
{
counts[i]+=counts[i-1];
}
//从后往前遍历，可以保持排序稳定性
int newarr[]=new int[arr.length];
for(int i=arr.length-1;i>=0;i--)
{
int index=counts[arr[i]/divider%10]-1;
newarr[index]=arr[i];
counts[arr[i]/divider%10]--;
}
for(int i=0;i<newarr.length;i++) arr[i]=newarr[i];
}
复杂度分析
最好最坏平均时间复制度：
O(d*(n+k))，d为最大值的位数，k是进制，一般都是十进制
空间复杂度：
O(n+k)
桶排序（BucketSort）
不同类型的数据，可以有不同的规则，没有固定的代码，只是一种方法论。
实现代码
double arr[]= {0.43,0.4,0.6,0.45,0.89,0.67};
//桶的规则，元素乘以总长度的值作为索引
List<Double> buckets[]=new List[arr.length];//可能有很多桶是空的
for(int i=0;i<arr.length;i++)
{
int bucketIndex=(int)arr[i]*arr.length;
if(buckets[bucketIndex]==null)
{
buckets[bucketIndex]=new LinkedList<>();
}
buckets[bucketIndex].add(arr[i]);
}
int index=0;
//对每个桶进行排序,可能有很多桶是空的
for(int i=0;i<buckets.length;i++)
{
if(buckets[i]==null) continue;
buckets[i].sort(null);
for(Double d:buckets[i])
{
arr[index++]=d;
}
}
复杂度分析
空间复杂度：O(n+m)m为桶的数量
时间复制度：
O(n+n*log(n/m))
扫一扫
1万+
到【灌水乐园】发言
