使用python实现兔子产子问题

一、问题描述

有一对兔子，从出生后的第3个月起每个月都生一对兔子。小兔子长到第3个月后每个月又生一对兔子，假设所有的兔子都不死，请使用python语言实现：30个月内每个月的兔子总对数为多少？

二、问题分析

兔子产子问题是一个有趣的古典数学问题，我们先来找一下兔子数的规律，

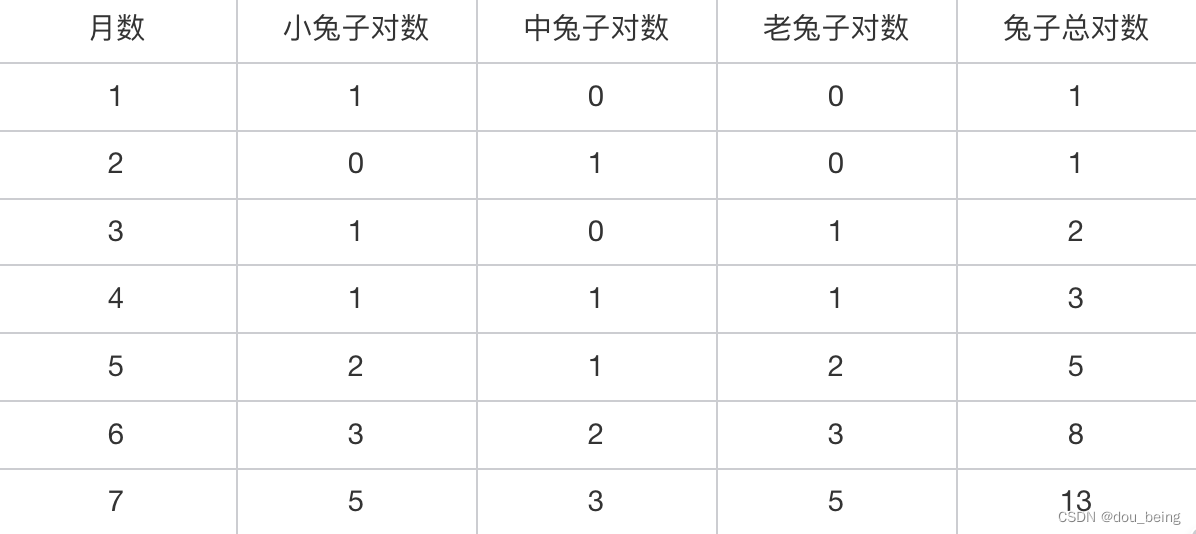
说明：不满1个月的兔子为小兔子，满1个月不满2个月的为中兔子，满3个月以上的为老兔子

可以看出，每个月的兔子总数依次为1，1，2，3，5，8，13…这就是Fibonacci数列。总结数列规律即为从前两个月的兔子对数可以推出第3个月的兔子对数。

三、算法思路

这是个典型的迭代循环问题，即是一个不断用新值取代变量的旧值，然后由变量旧值递推出变量新值的过程。算法可以描述为：迭代公式即为fib=fib1+fib2，其中fib为当前新求出的兔子对数，fib1为前一个月的兔子对数，fib2为前两个月的兔子对数，然后为下一次迭代做准备，进行如下的赋值fib2=fib1，fib1=fib，要注意赋值的次序；迭代次数由循环变量控制，为所求的月数

四、完整程序

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


if __name__ == "__main__":
    fib1 = 1
    fib2 = 1
    i = 3
    # 输出第一个月和第二个月的兔子对数
    print("%6d   %6d" % (fib1, fib2), end="  ")
    while i <= 30:
        # 迭代求出当前月份的兔子对数