1.题目链接:
假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm(下标从 1 开始),只要满足下述条
件 之一 ,该数组就是一个 优美的排列 :
perm[i] 能够被 i 整除
i 能够被 perm[i] 整除
给你一个整数 n ,返回可以构造的 优美排列 的 数量 。
• 示例 1:
输入:n = 2
输出:2
解释:
第 1 个优美的排列是 [1,2]:
- perm[1] = 1 能被 i = 1 整除
- perm[2] = 2 能被 i = 2 整除
第 2 个优美的排列是 [2,1]:
- perm[1] = 2 能被 i = 1 整除
- i = 2 能被 perm[2] = 1 整除
• 示例 2:
输入:n = 1
输出:1
• 提示:
1 <= n <= 15
3. 解法:
算法思路:
我们需要在每一个位置上考虑所有的可能情况并且不能出现重复。通过深度优先搜索的方式,不断地枚举每个数在当前位置的可能性,并回溯到上一个状态,直到枚举完所有可能性,得到正确的结果。我们需要定义一个变量 用来记录所有可能的排列数量,一个一维数组 visited 标记元素,然后从第一个位置开始进行递归;
递归函数设计:void backtrack(int index, int &n)
参数:index(当前需要处理的位置);
返回值:无;
函数作用:在当前位置填入一个合理的数字,查找所有满足条件的排列。
递归流程如下:
1. 递归结束条件:当 index 等于 n 时,说明已经处理完了所有数字,将当前数组存入结果中;
2. 在每个递归状态中,枚举所有下标 x,若这个下标未被标记,并且满足题目条件之一:
a. 将 visited[x] 标记为 1;
b. 对第 index+1 个位置进行递归;
c. 将 visited[x] 重新赋值为 0,表示回溯;
Java算法代码:
class Solution {
boolean[] check;
int ret;
public int countArrangement(int n) {
check = new boolean[n+1];
dfs(1,n);
return ret;
}
public void dfs(int pos, int n){
if(pos == n+1){
ret ++;
return ;
}
for(int i = 1;i<=n;i++){
if(check[i] == false && ( i % pos ==0 || pos%i==0)){
check[i] = true;
dfs(pos+1,n);
check[i] = false;
}
}
}
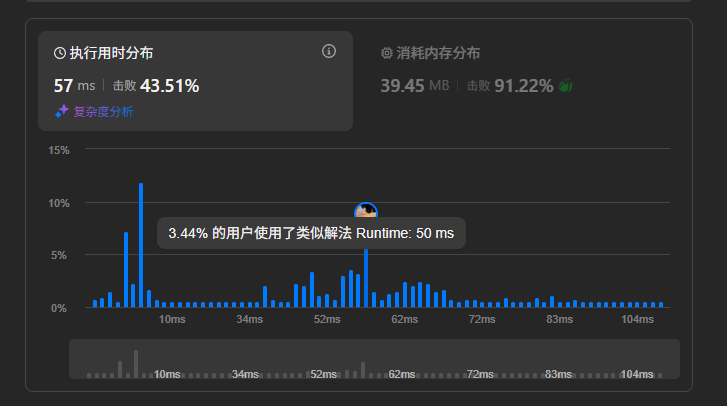
}运行结果:
递归展开:
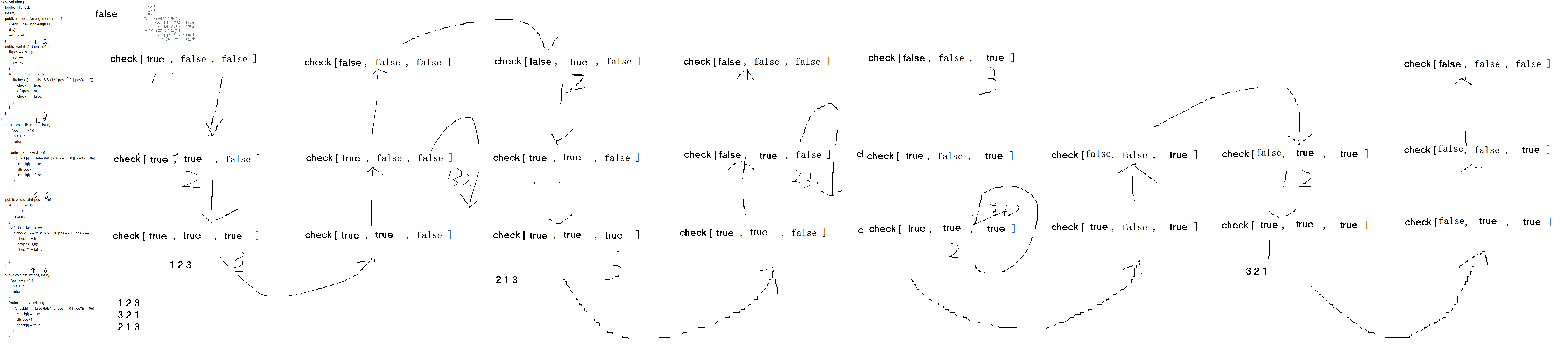
逻辑展开:需要去注意一些事情,(要去认真的读懂这个题目,就很容易理解后面的东西了)。
笔者刚开始做的时候,笔者理解错了这个题的意思(磨洋工)。
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!




















 118
118

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








