1.题目链接:
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
• 示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
• 示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
• 提示:
1 <= nums.length <= 8
-10 <= nums[i] <= 10
3. 解法:
算法思路:
因为题目不要求返回的排列顺序,因此我们可以对初始状态排序,将所有相同的元素放在各自相邻的位置,方便之后操作。因为重复元素的存在,我们在选择元素进行全排列时,可能会存在重复排列,例如:[1, 2, 1],所有的 下标排列 为:
| 1 | 123 |
按照以上下标进行排列的结果为:
| 1 | 121 |
可以看到,有效排列只有三种[1, 1, 2],[1, 2, 1],[2, 1, 1],其中每个排列都出现两次。因此,我们需要对相同元素定义一种规则,使得其组成的排列不会形成重复的情况:
1. 我们可以将相同的元素按照排序后的下标顺序出现在排列中,通俗来讲,若元素 s 出现 x 次,则排序后的第 2 个元素 s 一定出现在第 1 个元素 s 后面,排序后的第 3 个元素 s 一定出现在第 2 个元素s 后面,以此类推,此时的全排列一定不会出现重复结果。
2. 例如:a1=1,a2=1,a3=2,排列结果为 [1, 1, 2] 的情况只有一次,即 a1 在 a2 前面,因为 a2 不会 出现在 a1 前面从而避免了重复排列。
3. 我们在每一个位置上考虑所有的可能情况并且不出现重复;
4. *注意*:若当前元素的前一个相同元素未出现在当前状态中,则当前元素也不能直接放入当前状态 的数组,此做法可以保证相同元素的排列顺序与排序后的相同元素的顺序相同,即避免了重复排列 出现。
5. 通过深度优先搜索的方式,不断地枚举每个数在当前位置的可能性,并在递归结束时回溯到上一个状态,直到枚举完所有可能性,得到正确的结果。
递归函数设计:void backtrack(vector<int>& nums, int idx)参数:idx(当前需要填入的位置);
返回值:无;
函数作用:查找所有合理的排列并存储在答案列表中。
递归流程如下:
1. 定义一个二维数组 ans 用来存放所有可能的排列,一个一维数组 perm 用来存放每个状态的排列,一个一维数组 visited 标记元素,然后从第一个位置开始进行递归;
2. 在每个递归的状态中,我们维护一个步数 idx,表示当前已经处理了几个数字;
3. 递归结束条件:当 idx 等于 nums 数组的长度时,说明我们已经处理完了所有数字,将当前数组存入结果中;
4. 在每个递归状态中,枚举所有下标 i,若这个下标未被标记,并且在它之前的相同元素被标记过, 则使用 nums 数组中当前下标的元素:
a. 将 visited[i] 标记为 1;
b. 将 nums[i] 添加至 perm 数组末尾;
c. 对第 step+1 个位置进行递归;
d. 将 visited[i] 重新赋值为 0,并删除 perm 末尾元素表示回溯;
5. 最后,返回 ans。
Java算法代码:
class Solution {
List<Integer> path;
List<List<Integer>> ret;
boolean[] check;
public List<List<Integer>> permuteUnique(int[] nums) {
path = new ArrayList<>();
ret = new ArrayList<>();
check = new boolean[nums.length];
Arrays.sort(nums);
dfs(nums, 0);
return ret;
}
public void dfs(int[] nums, int pos){
if(pos == nums.length){
ret.add(new ArrayList<>(path));
return ;
}
for(int i =0; i< nums.length;i++) {
//剪枝
if(check[i] == false && (i == 0 || nums[i] != nums[i-1] || check[i-1] != false)){
path.add(nums[i]);
check[i] = true;
dfs(nums,pos + 1);
//回溯
path.remove(path.size() - 1);
check[i] =false;
}
}
}
}结果:
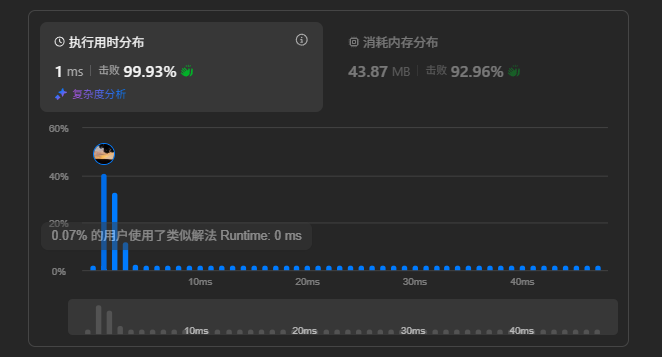
递归展开:
去仔细阅读我的流程,学习怎么画图(图画的好,更能传递自己的意思,能够帮助更好的解答这类题)。笔者的图画的也不一定很完美,有好的想法或者意见可以提出来(笔者会采纳的)。
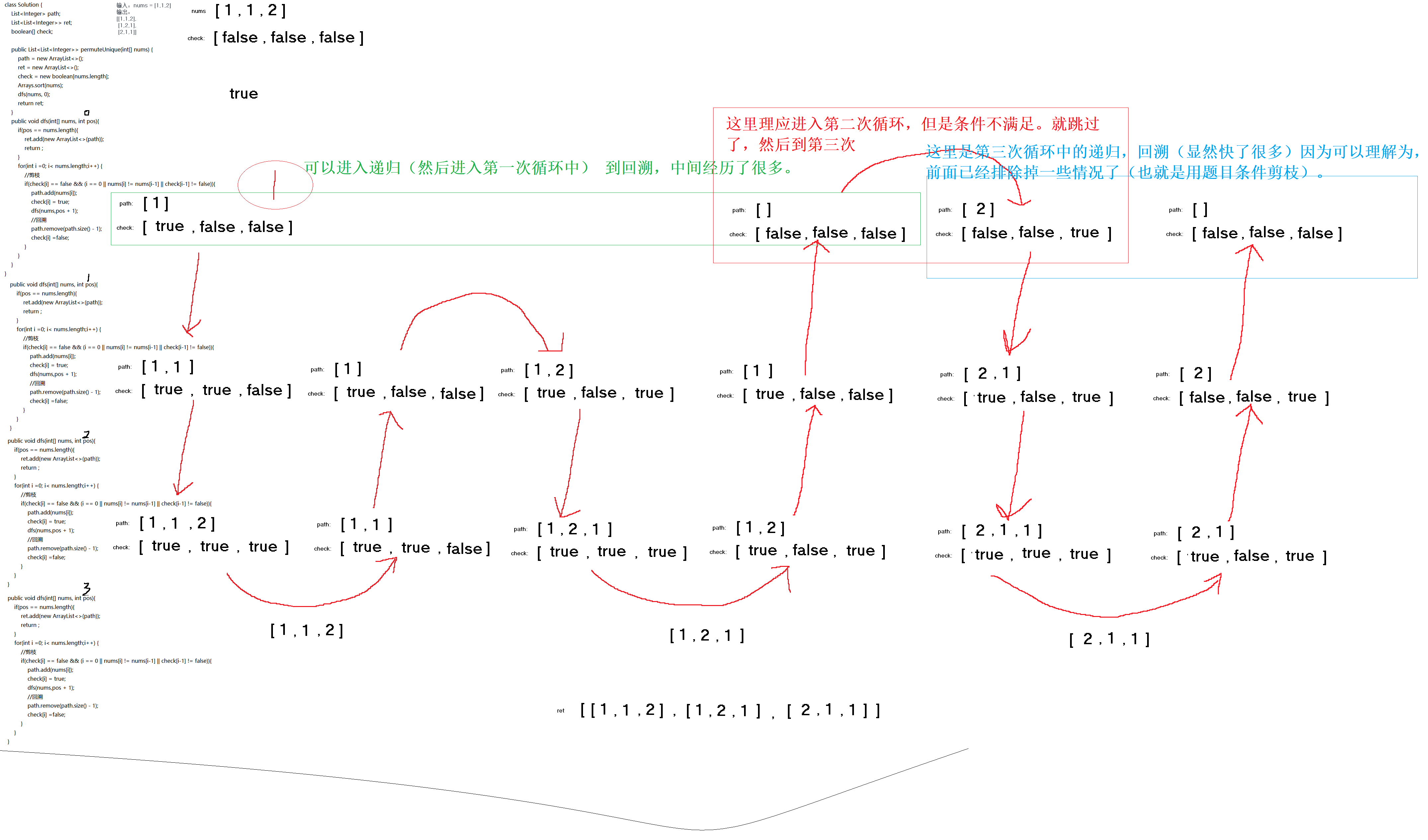
逻辑展开:
读者应该能够发现,笔者的逻辑展开,更像是讲讲给递归函数怎么做准备,和之前的不一样,这次的是补充了一些细节(比如,为何排序,等等)。

纸上得来终觉浅,绝知此事要躬行!!!
只看是学不会的,自己打开画图板(或者拿出纸),去动手,就会有感觉,不会决定被拦住了。
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!




















 605
605

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








