1.题目链接:
2.题目描述:
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。 每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
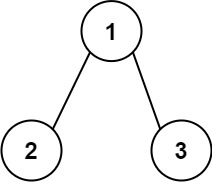
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:
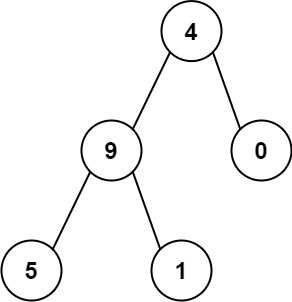
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
3. 解法(dfs - 前序遍历):
前序遍历按照根节点、左子树、右子树的顺序遍历二叉树的所有节点,通常用于子节点的状态依赖于父节点状态的题目。这里很显然要求根节点到叶节点数字之和,比较方便的是从根出发往下走(那就是前序遍历)。但是其他的遍历可以吗?也可以的,其他的遍历方式也是可以的。但是前序遍历会比较简单,简单在走到底(就可以算出来一条路的值,通过回溯。可以很快的到旁边的路)并且这里的处理逻辑是符合人类的各十百千。
算法思路:
在前序遍历的过程中,我们可以往左右子树传递信息,并且在回溯时得到左右子树的返回值。递归函数可以帮我们完成两件事:
1. 将父节点的数字与当前节点的信息整合到一起,计算出当前节点的数字,然后传递到下一层进行递归;
2. 当遇到叶子节点的时候,就不再向下传递信息,而是将整合的结果向上一直回溯到根节点。在递归结束时,根节点需要返回的值也就被更新为了整棵树的数字和。
算法流程:
递归函数设计:int dfs(TreeNode* root, int num)1. 返回值:当前子树计算的结果(数字和);
2. 参数 num:递归过程中往下传递的信息(父节点的数字);
3. 函数作用:整合父节点的信息与当前节点的信息计算当前节点数字,并向下传递,在回溯时返回当前子树(当前节点作为子树根节点)数字和。
递归函数流程:
1. 当遇到空节点的时候,说明这条路从根节点开始没有分支,返回 0;
2. 结合父节点传下的信息以及当前节点的 val,计算出当前节点数字 sum;
3. 如果当前结点是叶子节点,直接返回整合后的结果 sum;
4. 如果当前结点不是叶子节点,将 sum 传到左右子树中去,得到左右子树中节点路径的数字和,然 后相加后返回结果。
Java算法代码:
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root, 0);
}
public int dfs(TreeNode root,int preSum){
preSum = preSum*10 + root.val;
if(root.left == null && root.right==null) return preSum;
int ret = 0;
if(root.left !=null) ret+= dfs(root.left,preSum);
if(root.right !=null) ret+= dfs(root.right,preSum);
return ret;
}
}
运行结果:
递归展开:
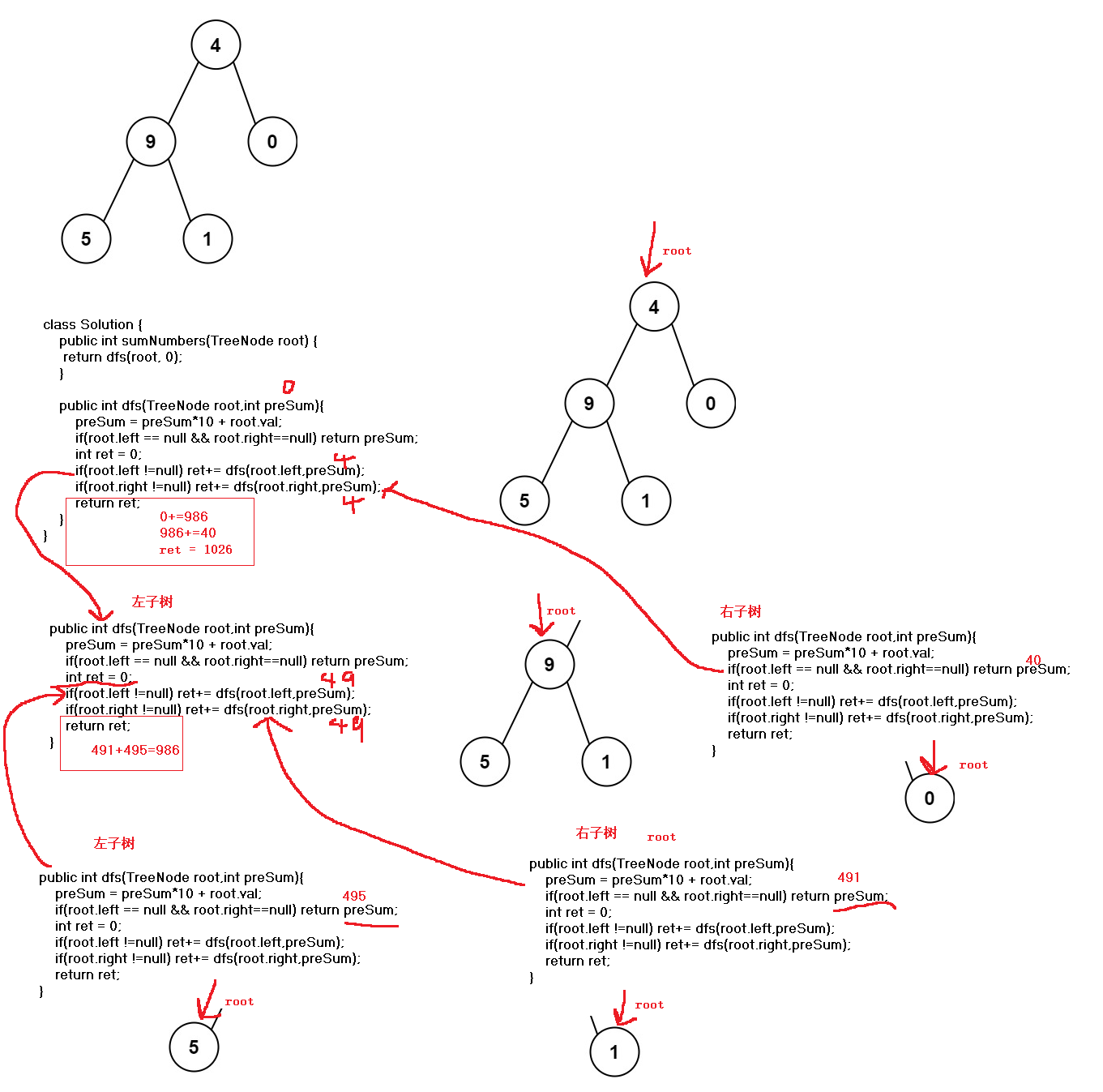
逻辑展开:

思考下,这个递归函数,和前面的题目有点不一样了。
比如,这里是通过preSum来完成,也就是说不是直接利用,而是递归函数中来完成任务(也就是计算根节点到某条具体的路的值是递归函数完成的)前面的题目是,通过递归函数来得到我们需要的数据,然后自己处理。
这道题是: 递归函数处理+我们进一步处理。
之前题目:递归函数给我们数值+我们处理数值。
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!




















 157
157

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








