1.题目链接:面试题 08.06. 汉诺塔问题 - 力扣(LeetCode)
2.题目描述:
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开 始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动 圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = []
输出:C = [2, 1, 0]
示例2:
输入:A = [1, 0], B = [], C = []
输出:C = [1, 0]
提示:
A中盘子的数目不大于14个。
3.解法(递归):
算法思路:
这是一道递归方法的经典题目,我们可以先从最简单的情况来考虑:
假设 n = 1,只有一个盘子,很简单,直接把它从 A 中拿出来,移到 C 上;
如果 n = 2 呢?这时候我们就要借助 B 了,因为小盘子必须时刻都在大盘子上面,共需要 3 步(为了方便叙述,记 A 中的盘子从上到下为 1 号,2 号):
a. 1 号盘子放到 B 上;
b. 2 号盘子放到 C 上;
c. 1 号盘子放到 C 上。
至此,C 中的盘子从上到下为 1 号, 2 号。
如果 n > 2 呢?这是我们需要用到 n = 2 时的策略,将 A 上面的两个盘子挪到 B 上,再将最大的盘子挪到 C 上,最后将 B 上的小盘子挪到 C 上就完成了所有步骤。例如 n = 3 时如下图:

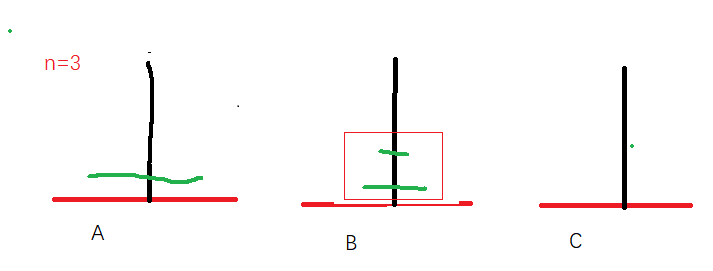
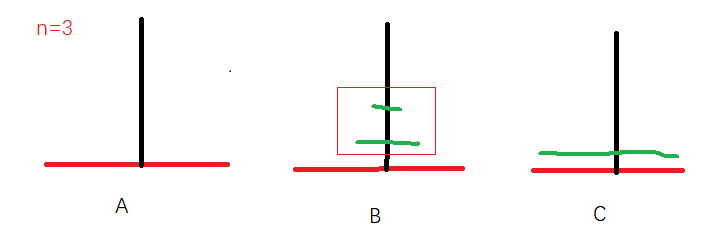
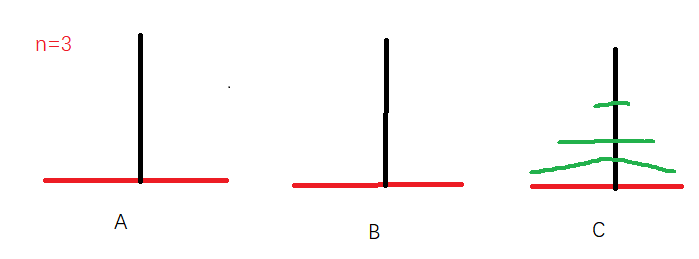
请注意,这里看作一起。后面会做解释,你可以在逻辑上认为是拆分为两个,大盘子一个,其余的是另一个盘子。
因为 A 中最后处理的是最大的盘子,所以在移动过程中不存在大盘子在小盘子上面的情况。则本题可以被解释为:
1. 对于规模为 n 的问题,我们需要将 A 柱上的 n 个盘子移动到C柱上。
2. 规模为 n 的问题可以被拆分为规模为 n-1 的子问题:
a. 将 A 柱上的上面 n-1 个盘子移动到B柱上。
b. 将 A 柱上的最大盘子移动到 C 柱上,然后将 B 柱上的 n-1 个盘子移动到C柱上。 3. 当问题的规模变为 n=1 时,即只有一个盘子时,我们可以直接将其从 A 柱移动到 C 柱。
•需要注意的是,步骤 2.b 考虑的是总体问题中的子问题b 情况。在处理子问题的 子问题b 时,我们应该将 A 柱中的最上面的盘子移动到 C 柱,然后再将 B 柱上的盘子移动到 C 柱。在处理总体问题的 子问题b 时,A 柱中的最大盘子仍然是最上面的盘子,因此这种做法是通用的。
算法流程:
递归函数设计:void hanotaa(vector<int>& A, vector<int>& B, vector<int>& C, int n)
1.返回值:无;(这个函数只做事情,不需要传递东西)
2. 参数:三个柱子上的盘子,当前需要处理的盘子个数(当前问题规模)。
3. 函数作用:将 A 中的上面 n 个盘子挪到 C 中。
递归函数流程:
1. 当前问题规模为 n=1 时,直接将 A 中的最上面盘子挪到 C 中并返回;(这里是出口)
2. 递归将 A 中最上面的 n-1 个盘子挪到 B 中;
3. 将 A 中最上面的一个盘子挪到 C 中;
4. 将 B 中上面 n-1 个盘子挪到 C 中。
Java代码:
class Solution {
public void hanota(List<Integer> a, List<Integer> b, List<Integer> c) {
dfs(a,b,c,a.size());
// 不讲武德的办法
//
//for(int x:a) c.add(x);
}
public void dfs(List<Integer> a, List<Integer> b, List<Integer> c, int n){
if(n == 1){ //递归出口
c.add(a.remove(a.size() -1));
return ;
}
dfs(a,c,b,n-1);//这里是将A中最上面的n-1个盘子挪到B中
c.add(a.remove(a.size() -1));//将A中最上面的一个盘子挪到C中。
dfs(b,a,c,n-1);//将B中上面n-1个盘子挪到C中。
}
}
递归展开图分析:从n=3即刻说明问题;
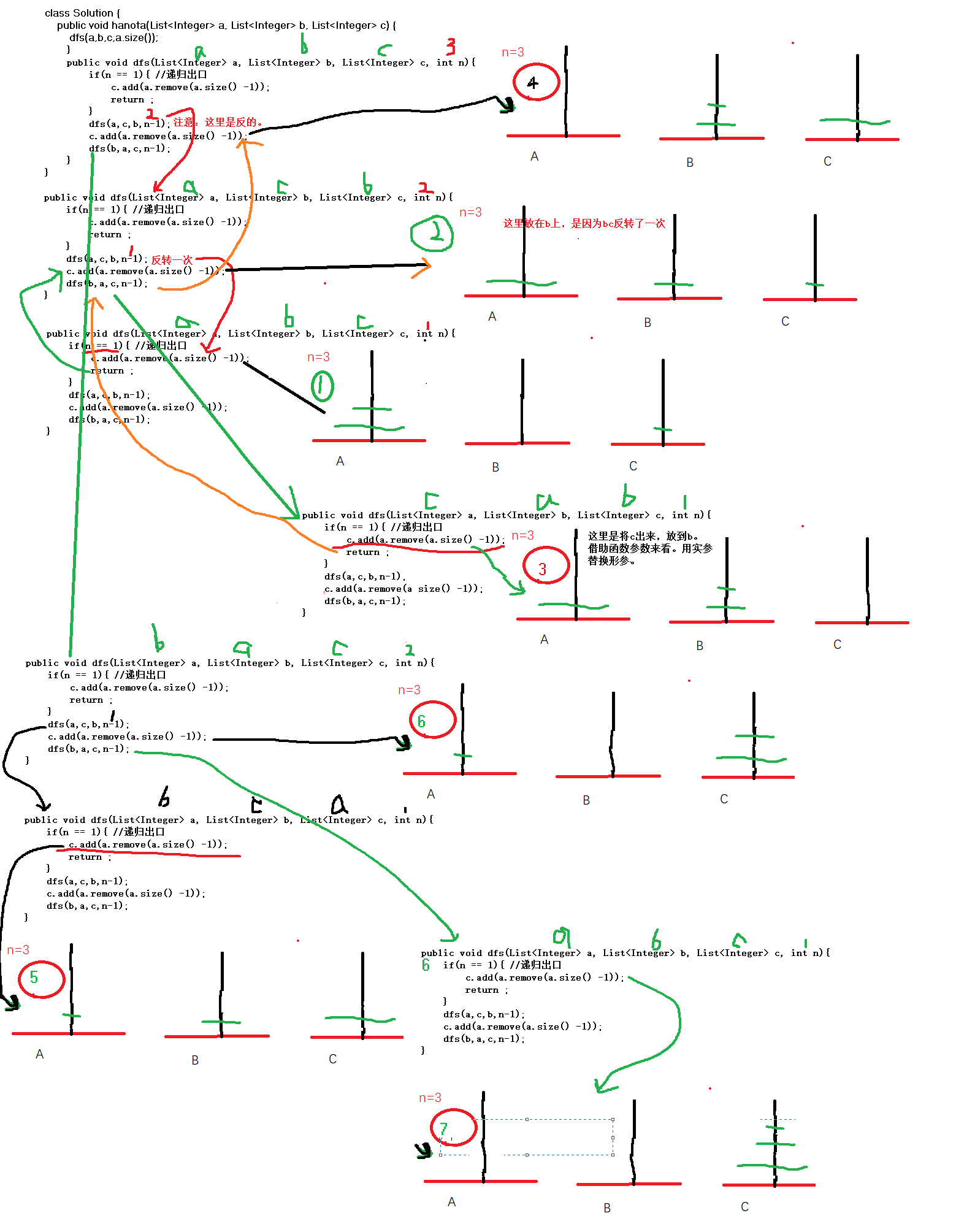
希望读者可以认真的动手画一画,来领悟其中的细节。
下面是人脑的思考过程(实际上人脑也有这个过程,但是自己是很难将这个过程理解为递归,而是换换换,再往C或者B放都是需要思考,如果n=4,甚至更多,脑子就不够用了。
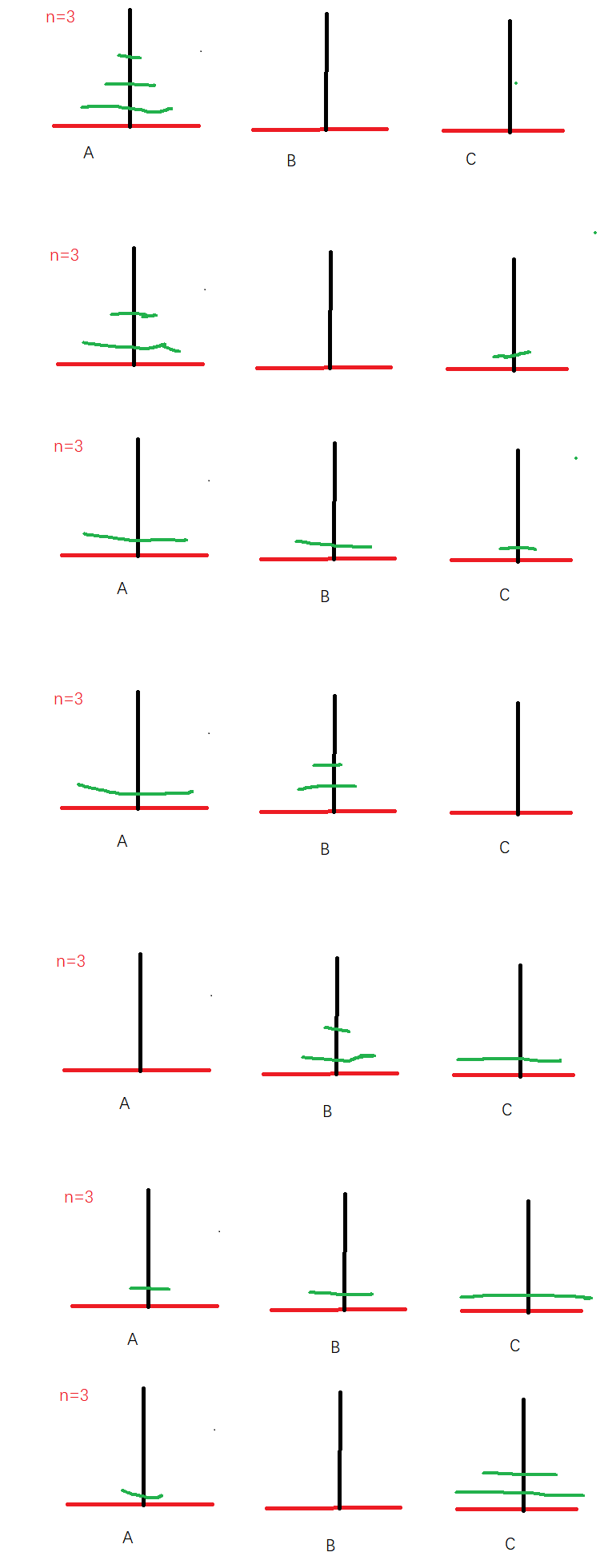
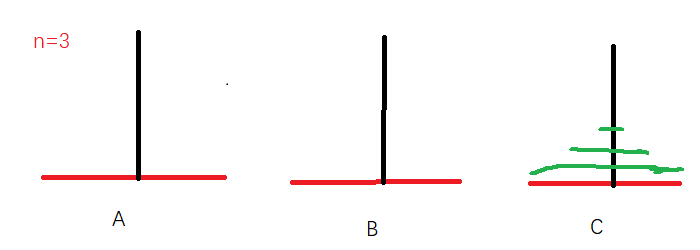
a. 问题可以被划分为规模更小的子问题,并且这些子问题具有与原问题相同的解决方法。 b. 当我们知道规模更小的子问题(规模为 n - 1)的解时,我们可以直接计算出规模为 n 的问题的解。
c. 存在一种简单情况,或者说当问题的规模足够小时,我们可以直接求解问题。
一般的递归求解过程如下:
a. 验证是否满足简单情况。
b. 假设较小规模的问题已经解决,解决当前问题。上述步骤可以通过数学归纳法来证明。
从这里抽象下:
最开始说个一句话,将A上的盘子分为下面的一个和上面的整体(看作两个盘子),然后用两个盘子的解决方法去解决问题(也就是需要用到n=2时候的策略)。
还有,请相信你的递归函数,他是可以做到的(在这里是相信,即使上面的盘子有很多,但通过n-1的递归调用时,可以将上面的盘子移动到C的位置)。
可以想想我前面提到的不讲武德的方式,为什么可以完成任务,并且代码很简单(给面试官可千万不要用这种方法)。
for(int x:a) c.add(x);c.addAll(a);
a.clear();感兴趣的可以试试其他的操作,可以去验证这里的底层是什么。
从这里能发现Java的List是尾插有序结构;
汉诺塔题目最终只判断内容和顺序对不对;
---------------------------------------------------------------------------------------------------------------------------------
记住,相信你的递归函数,它可以做到!
记住,不理解时候,去尝试手动展开!
记住,逻辑展开(你不可能对所有的题目都进行手动展开)!




















 2769
2769

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








