基础≠简单！7 大基础算法实战入门完全指南（含经典例题 + 易错点解析）

最新推荐文章于 2026-01-08 22:28:34 发布

原创最新推荐文章于 2026-01-08 22:28:34 发布 · 806 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #笔记 #蓝桥杯 #经验分享

蓝桥杯备战参考指南专栏收录该内容

4 篇文章

订阅专栏

目录

引言：为何“基础算法”不能被轻视？

一、模拟：照着题目“动手写”

原理讲解

经典例题：多项式输出（洛谷 P1067）

解法：

AC代码：

⚠️ 易错点提示

进阶例题：蛇形方阵（洛谷 P5731）

技巧：方向向量 + 边界检测

解法：

参考代码：

二、高精度：当 long long 也不够用

原理讲解

四则运算模板

1. 高精度加法（洛谷 P1601）

解法：

参考代码：

2. 高精度减法（洛谷 P2142）

3. 高精度乘法（洛谷 P1303）

4. 高精度除法（洛谷 P1480）— 仅支持高精 ÷ 低精

⚠️ 易错点提示

三、枚举：暴力的艺术

原理讲解

例题：铺地毯（洛谷 P1003）

参考代码块：

二进制枚举：子集生成（LeetCode 78）

参考代码块：

⚠️ 易错点提示

四、前缀和：O(1) 查询区间和

原理讲解

一维前缀和（牛客模板）

二维前缀和（牛客模板）

应用题：激光炸弹（洛谷 P2880）

⚠️ 易错点提示

五、差分：O(1) 区间修改

🧠 原理讲解

5.1 ⼀维差分

⚠️ 易错点提示

六、双指针：滑动窗口优化暴力

原理讲解

📌 经典题型

⚠️ 易错点提示

七、二分：从查找 → 答案

原理讲解

二分答案：最大值最小 / 最小值最大

⚠️ 易错点提示

总结：基础算法学习路径图

刷题建议

思考题：

引言：为何“基础算法”不能被轻视？

很多初学者看到 “模拟”、“枚举” 就以为是“水题”，直接跳过。但事实是——
基础 ≠ 简单！
这些算法是所有高级技巧（如 DP、图论、网络流）的基石，更是 NOIP、蓝桥杯、LeetCode 周赛 中高频出现的“签到题”来源。

轻视基础，等于放弃登顶的可能。

本文是《算法基础篇》第 1 篇博客，用 原理 + 例题 + 代码 + 易错点 四步法，带你系统掌握 模拟、高精度、枚举、前缀和、差分、双指针、二分 七大基础算法。

一、模拟：照着题目“动手写”

原理讲解

模拟题 的核心是：题目让你做什么，你就照着写代码。重点考察 逻辑拆解能力 和 边界处理能力。

经典例题：多项式输出（洛谷 P1067）

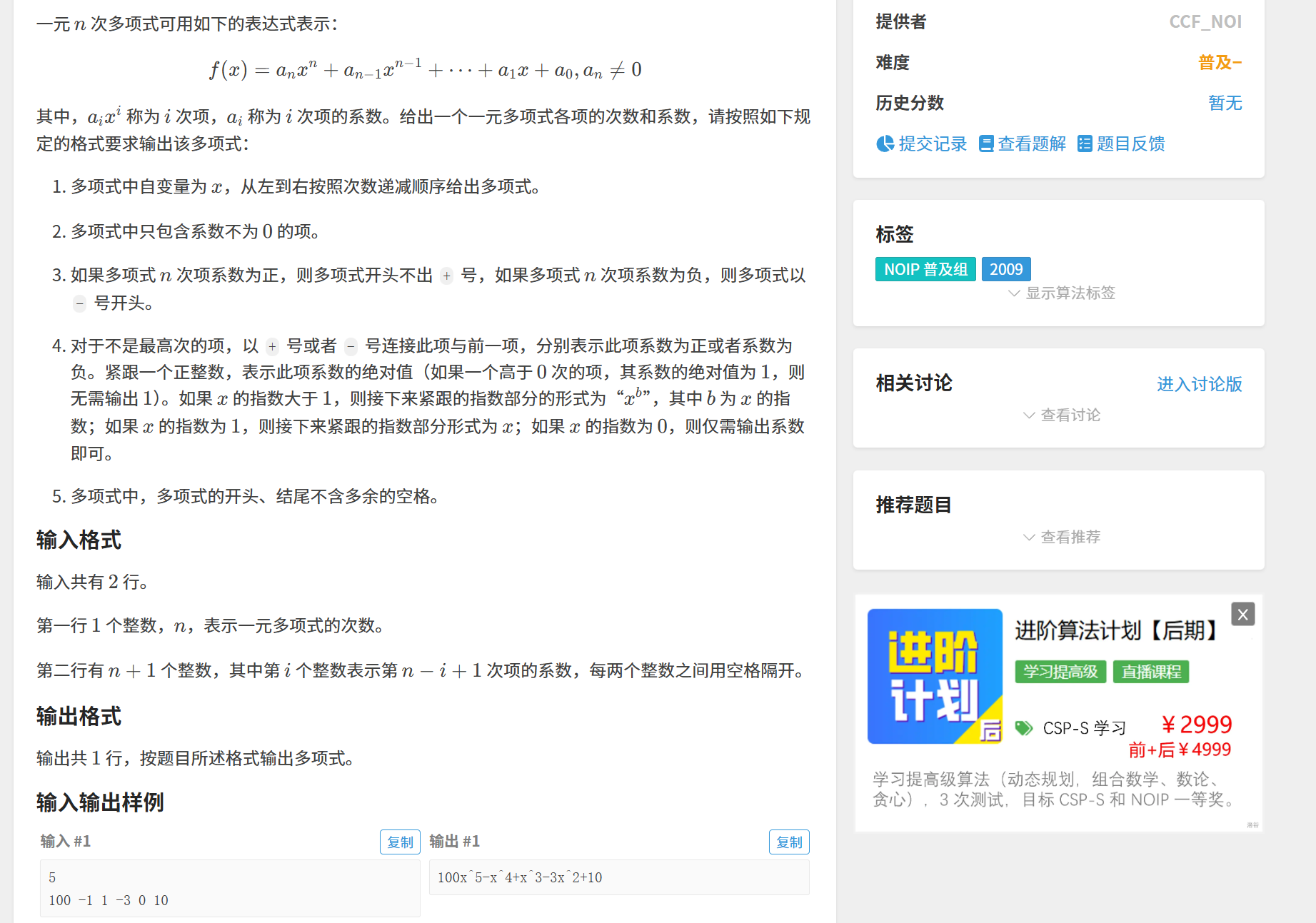
题目大意：给定一元 n 次多项式的系数，按规范格式输出（如 100x^5-x^4+x^3-3x^2+10）。

输入：
5
100 -1 1 -3 0 10

输出：
100x^5-x^4+x^3-3x^2+10

解法：

模拟+分类讨论，对于⼀元n次⽅程的的最终结果，我们仅需按照顺序，考虑每⼀项的三件事情：符号 + 系数 + 次数。

处理「符号」：

◦ 如果系数⼩于0 ，直接输出 "-"；

◦ 如果系数⼤于0 ，除了⾸项不输出 "+"，其余全部输出 "+"。

处理「系数」：

◦ 先取⼀个绝对值，因为正负的问题已经处理过了；

◦ 当系数不等于 1 ，直接输出这个数；

◦ 但是当系数为 1 ，且是最后⼀项的时候，这个 1 也是需要输出的；其余情况下的 1 不需要输出。

处理「次数」：

◦ 次数⼤于 1 ，输出 "x^" + 对应的次数；

◦ 次数等于 1 ，输出 "x"；

◦ 次数⼩于 1 ，什么也不输出。

AC代码：

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    int n; cin >> n;
    for (int i = n; i >= 0; i--) {
        int a; cin >> a;
        if (a == 0) continue; // 跳过系数为0的项

        // 1. 处理符号
        if (a < 0) cout << '-';
        else if (i != n) cout << '+'; // 首项不输出+

        // 2. 处理系数
        a = abs(a);
        if (a != 1 || (a == 1 && i == 0)) cout << a;

        // 3. 处理次数
        if (i == 0) continue;
        else if (i == 1) cout << 'x';
        else cout << "x^" << i;
    }
    return 0;
}

⚠️ 易错点提示

首项正数不能加 +，但非首项负数要输出 -；
系数为 ±1 且非常数项时，不输出 1；
常数项（i=0）只输出系数，不输出 x。

进阶例题：蛇形方阵（洛谷 P5731）

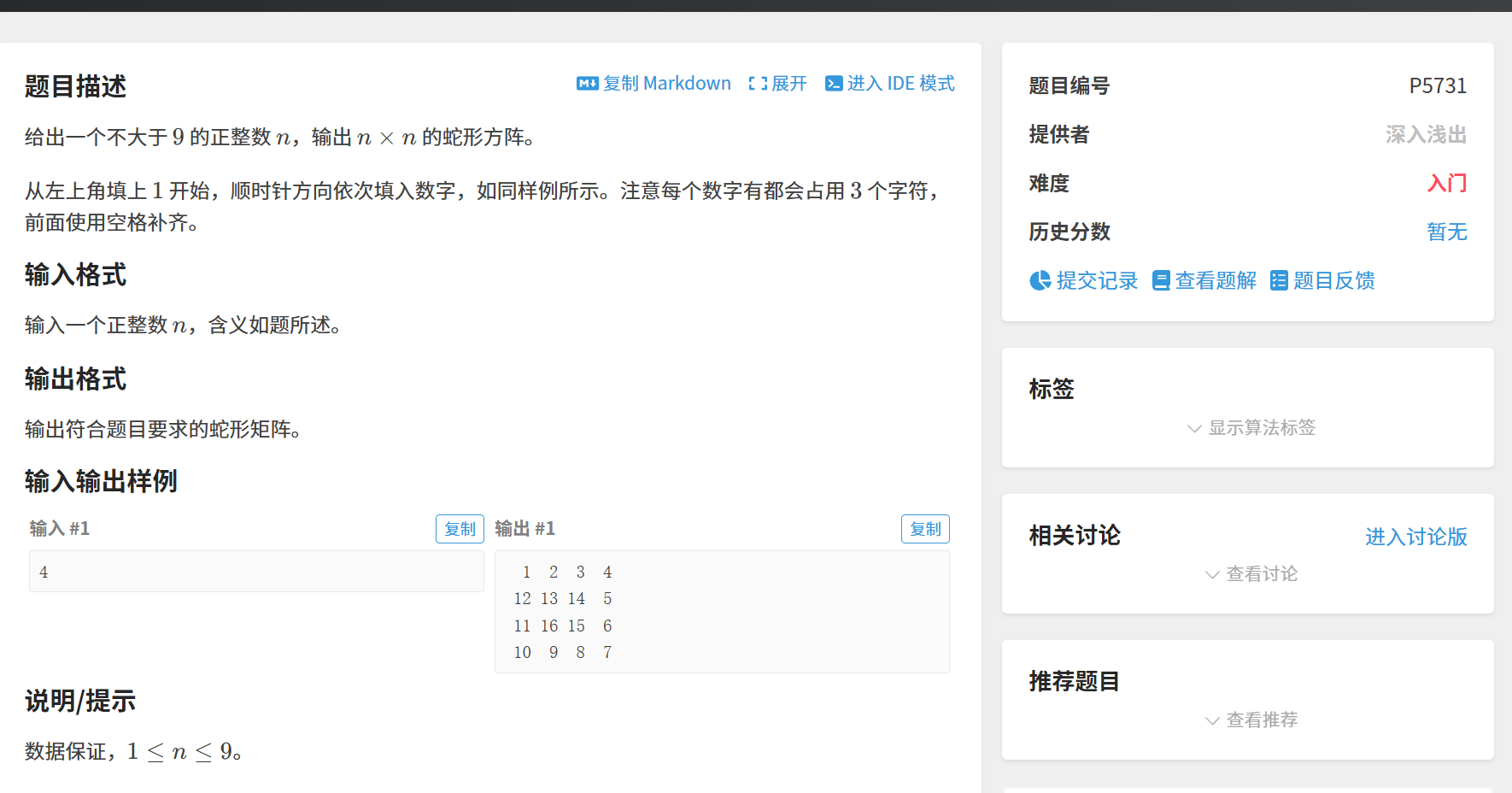
用方向数组 (0,1)→(1,0)→(0,-1)→(-1,0) 模拟填数。

技巧：方向向量 + 边界检测

越界或已填 → 转向；
用 dx[], dy[] 数组简化移动逻辑。

解法：

模拟填数的过程。

在⼀个矩阵中按照⼀定规律填数的通⽤解法：

• 定义⽅向向量，⽐如本题⼀共四个⽅向，分别是右、下、左、上，对应： (0, 1)、(1, 0)、(0, −1)、(−1, 0)

• 循环填数的规则：

◦ 朝⼀个⽅向⾛，⼀边⾛⼀边填数，直到越界；

◦ 越界之后，结合定义的⽅向向量，求出下⼀轮应该⾛的⽅向以及应该到达的正确位置；

◦ 重复上述过程，直到把所有的数填完为⽌。

参考代码：


#include <iostream>
using namespace std;
const int N = 15;
// 定义 右，下，左，上 四个⽅向 
int dx[] = { 0, 1, 0, -1 };
int dy[] = { 1, 0, -1, 0 };
int arr[N][N];
int main()
{
	int n; cin >> n;
	// 模拟填数过程 
	int x = 1, y = 1; // 初始位置 
	int cnt = 1; // 当前位置要填的数 
	int pos = 0; // 当前的⽅向 
	while (cnt <= n * n)
	{
		arr[x][y] = cnt;
		// 计算下⼀个位置 
		int a = x + dx[pos], b = y + dy[pos];
		// 判断是否越界 
		if (a < 1 || a > n || b < 1 || b > n || arr[a][b])
		{
			// 更新出正确的该⾛的位置 
			pos = (pos + 1) % 4;
			a = x + dx[pos], b = y + dy[pos];
		}
		x = a, y = b;
		cnt++;
	}
	// 输出 
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			printf("%3d", arr[i][j]);
		}
		puts("");
	}
	return 0;
}

二、高精度：当 long long 也不够用

原理讲解

高精度算法 = 用数组模拟竖式运算。核心思想：

逆序存储（低位在前，方便进位）；
逐位运算 + 进位/借位处理。

⾼精度算法本质上还是模拟算法，⽤代码模拟⼩学列竖式计算加减乘除的过程。

四则运算模板

1. 高精度加法（洛谷 P1601）

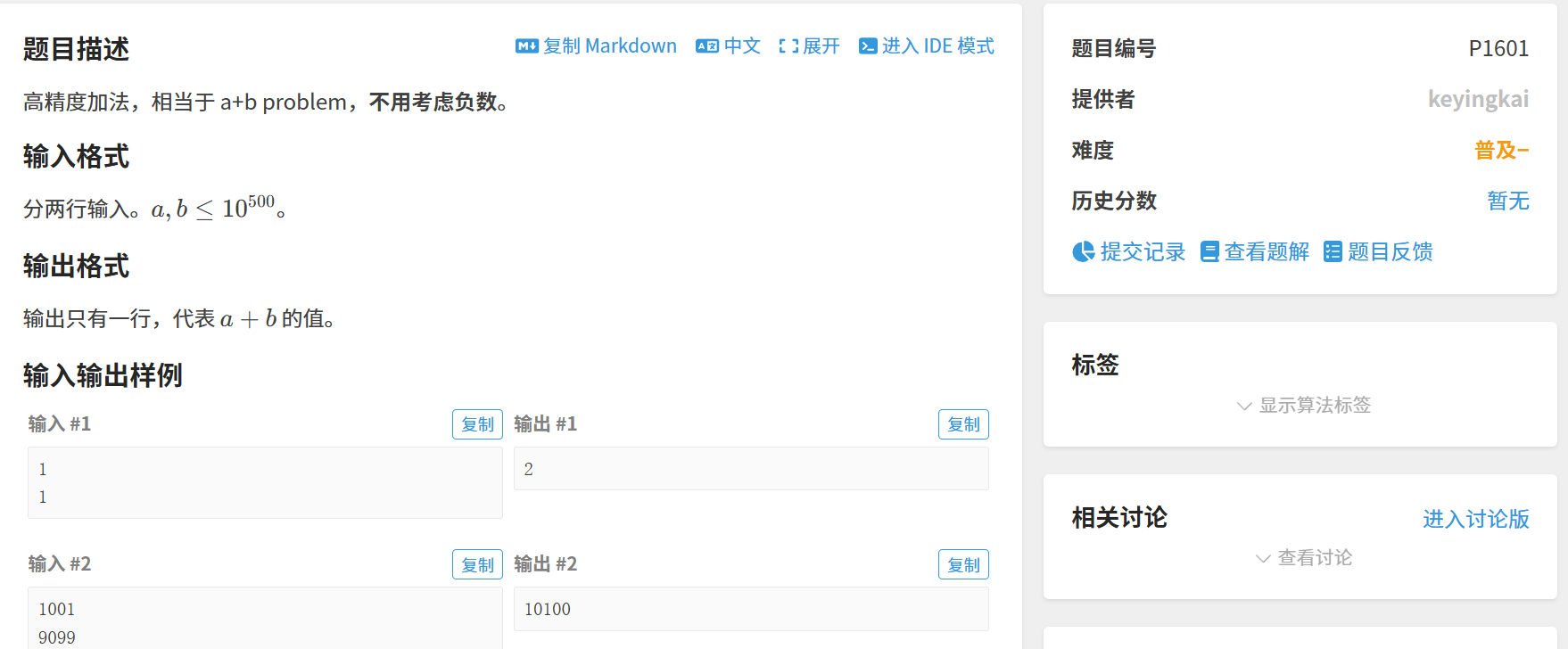
解法：

模拟⼩学「列竖式」计算「两数相加」的过程。

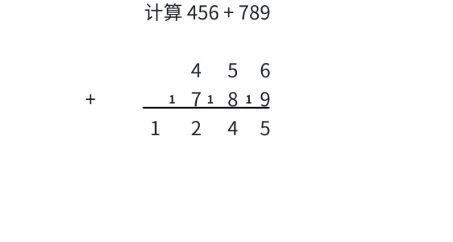
1. ⽤字符串读⼊数据；

2. 将字符串的每⼀位拆分，逆序放在数组中；

3. 模拟列竖式计算的过程：

a. 对应位累加；

b. 处理进位；

c. 处理余数。

4. 处理结果的位数。

参考代码：

#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
// ⾼精度加法的模版 - c = a + b; 
void add(int c[], int a[], int b[])
{
	for (int i = 0; i < lc; i++)
	{
		c[i] += a[i] + b[i]; // 对应位相加，再加上进位 
		c[i + 1] += c[i] / 10; // 处理进位 
		c[i] %= 10; // 处理余数 
	}
	if (c[lc]) lc++;
}
int main()
{
	string x, y; cin >> x >> y;
	// 1. 拆分每⼀位，逆序放在数组中 
	la = x.size(); lb = y.size(); lc = max(la, lb);
	for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
	for (int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
	// 2. 模拟加法的过程 
	add(c, a, b); // c = a + b

	// 输出结果 
	for (int i = lc - 1; i >= 0; i--) cout << c[i];
	return 0;
}

2. 高精度减法（洛谷 P2142）

先比大小：位数不同看长度，相同看字典序；
借位处理：if (c[i] < 0) { c[i] += 10; c[i+1]--; }

3. 高精度乘法（洛谷 P1303）

无进位相乘：c[i+j] += a[i] * b[j]；
统一处理进位。

4. 高精度除法（洛谷 P1480）— 仅支持高精 ÷ 低精

从高位到低位，模拟手工除法；
t = t * 10 + a[i]，c[i] = t / b，t %= b。

⚠️ 易错点提示

减法要处理负号；
乘法结果长度最多是 len1 + len2；
除法要清前导零。

三、枚举：暴力的艺术

原理讲解

枚举 = 把所有可能情况列出来。虽“暴力”，但常因 剪枝 / 逆序枚举 而高效。

例题：铺地毯（洛谷 P1003）

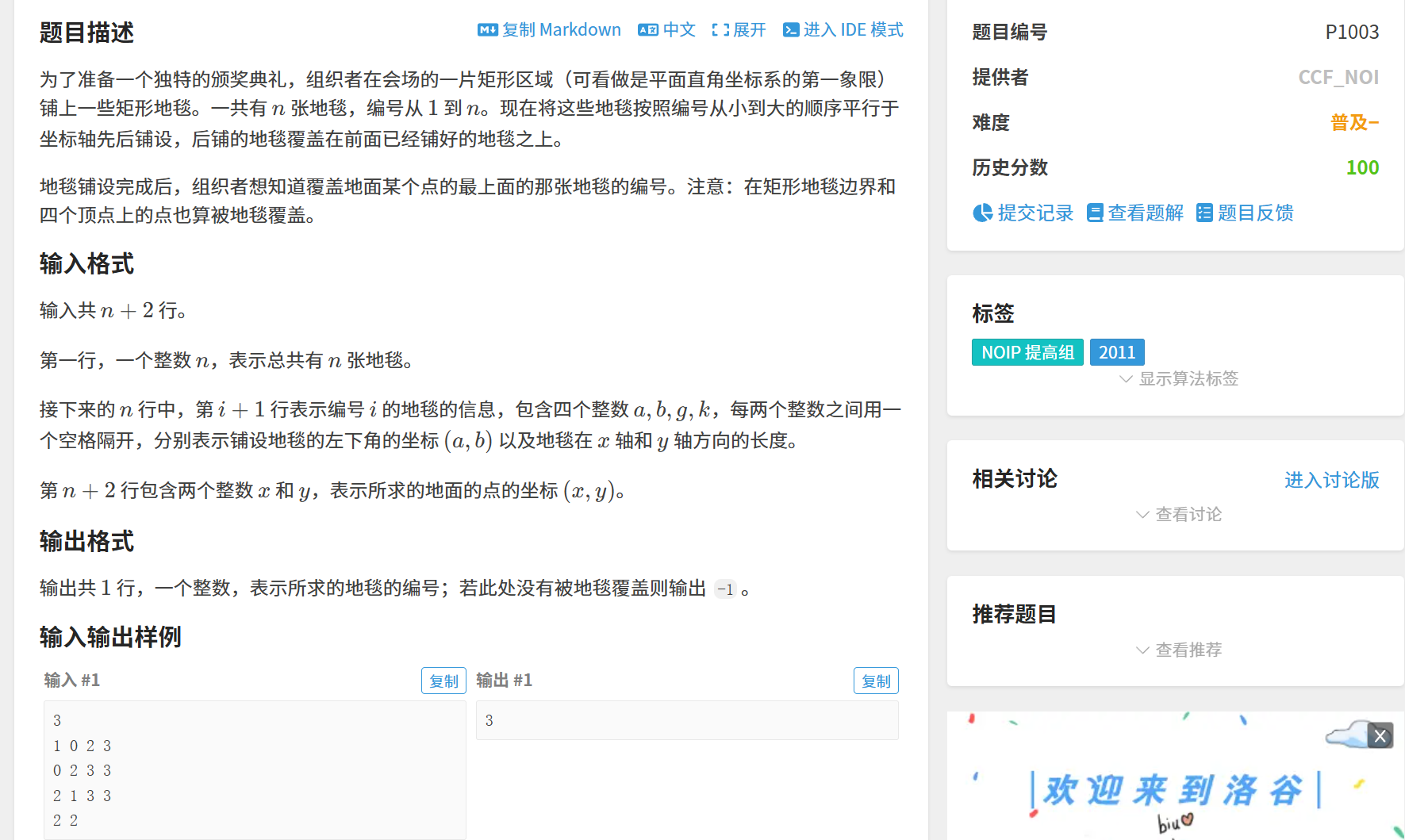
逆序枚举 地毯，第一个覆盖 (x,y) 的即为答案（后铺的在上层）

参考代码块：

for (int i = n; i >= 1; i--) {
    if (a[i] <= x && b[i] <= y && 
        a[i] + g[i] >= x && b[i] + k[i] >= y) {
        return i;
    }
}

二进制枚举：子集生成（LeetCode 78）

用 0~(1<<n)-1 的每个数的二进制位表示是否选该元素。

参考代码块：

for (int st = 0; st < (1 << n); st++) {
    vector<int> tmp;
    for (int i = 0; i < n; i++)
        if ((st >> i) & 1) tmp.push_back(nums[i]);
    ret.push_back(tmp);
}

⚠️ 易错点提示

逆序枚举可提前终止，节省时间；
二进制枚举状态数为 2^n，n ≤ 20 才安全。

四、前缀和：O(1) 查询区间和

原理讲解

前缀和 = 空间换时间，预处理后 区间和查询 O(1)。

一维前缀和（牛客模板）

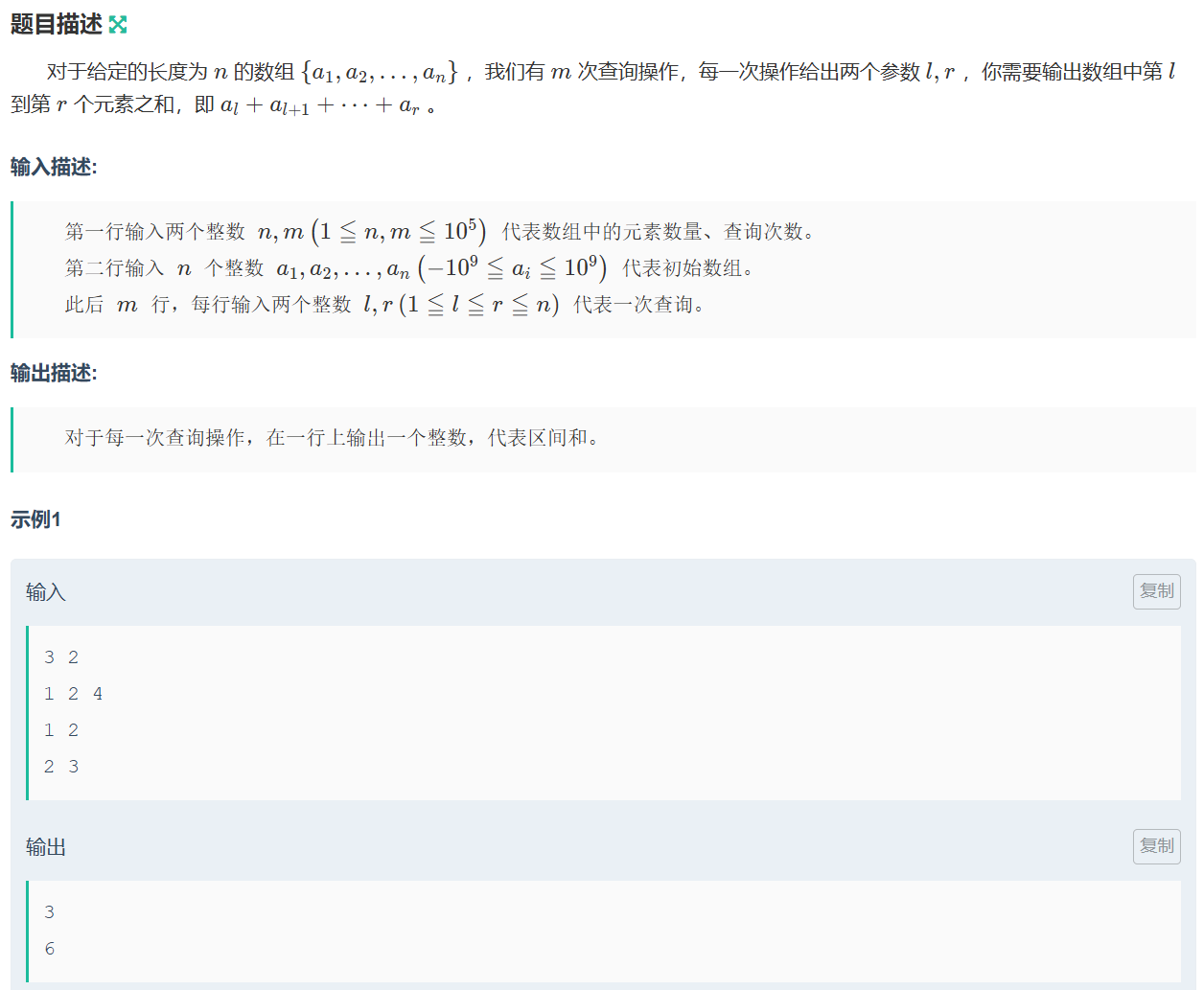
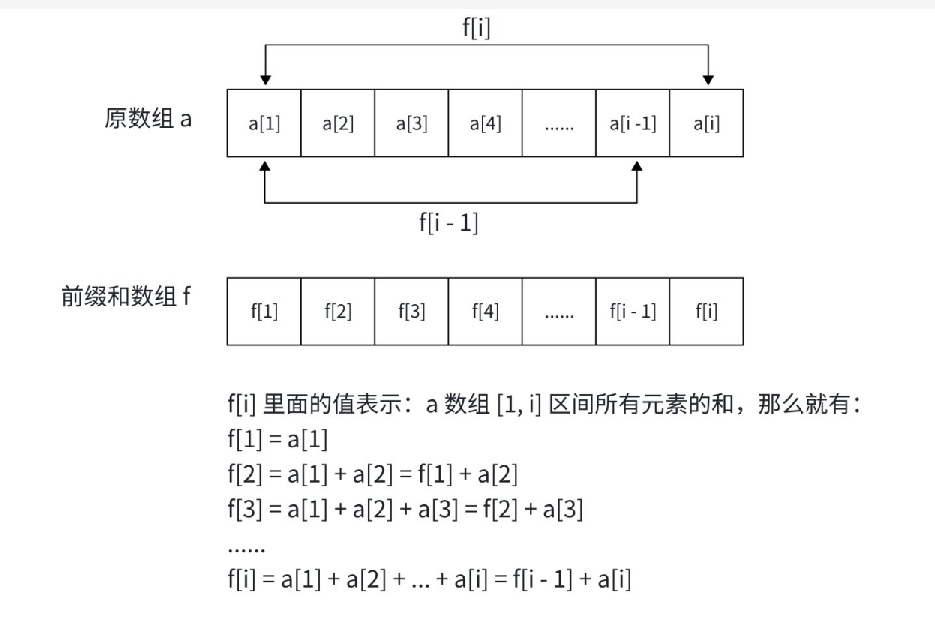
前缀和模板题，直接套⽤「公式」创建前缀和数组，然后利⽤前缀和数组的「性质」处理q次查询。

构建：f[i] = f[i-1] + a[i]
查询：[l, r] 和 = f[r] - f[l-1]

二维前缀和（牛客模板）

构建：
f[i][j] = f[i-1][j] + f[i][j-1] - f[i-1][j-1] + a[i][j]
查询：
子矩阵和 = f[x2][y2] - f[x1-1][y2] - f[x2][y1-1] + f[x1-1][y1-1]

应用题：激光炸弹（洛谷 P2880）

枚举所有 R×R 正方形，用二维前缀和快速求和。

可以⽤⼀个⼆维矩阵将所有⽬标的价值存起来，其中 a[i][j] 就表⽰ [i, j] 位置的⽬标价值之和。⼀颗炸弹能够获得的价值正好是⼀个R*R ⼤⼩的⼀个正⽅形内所有⽬标的价值总和，那么我们可以求出 a 矩阵的前缀和矩阵，然后枚举所有边⻓为R 的⼦正⽅形的价值之和，求出⾥⾯的最⼤值即可。

#include <iostream>
using namespace std;
const int N = 5010;
int n, m;
int a[N][N];
int f[N][N]; // 前缀和矩阵 
int main()
{
	cin >> n >> m;
	while (n--)
	{
		int x, y, v; cin >> x >> y >> v;
		x++, y++; // 下标从 1 开始计数 
		a[x][y] += v; // 同⼀个位置有可能有多个⽬标 
	}
	n = 5001;
	// 预处理前缀和矩阵 
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
		{
			f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];
		}
	}
	int ret = 0;
	m = min(m, n); // 如果 m 很⼤，相当于就是把整个区域全部摧毁 
	// 枚举所有边⻓为 m 的正⽅形 
	for (int x2 = m; x2 <= n; x2++)
	{
		for (int y2 = m; y2 <= n; y2++)
		{
			int x1 = x2 - m + 1, y1 = y2 - m + 1;
			ret = max(ret, f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 -
				1][y1 - 1]);
		}
	}
	cout << ret << endl;
	return 0;
}

⚠️ 易错点提示

坐标从 1 开始，避免越界；
边长 R 可能 > 5000，此时答案 = 总价值。

五、差分：O(1) 区间修改

🧠 原理讲解

差分是前缀和的逆运算，用于高效区间加。

是经典的⽤空间替换时间的做法。学完差分之后，⼤家会发现，前缀和与差分是⼀对互逆的运算。

5.1 ⼀维差分

差分模板题，先「创建」差分数组，然后根据差分数组的「性质」处理次区间修改，最后「还原」出来原始的数组。

修改 [l, r] += k：
f[l] += k; f[r+1] -= k;
还原：对 f 做前缀和

创建差分数组，根据定义：

f[i] = a[i] − a[i − 1]

也可以根据差分数组的性质：f[i] + = a[i], f[i + 1] − = a[i]

根据差分数组的性质处理 q 区间修改：f[L] + = c, f[R + 1] − = c

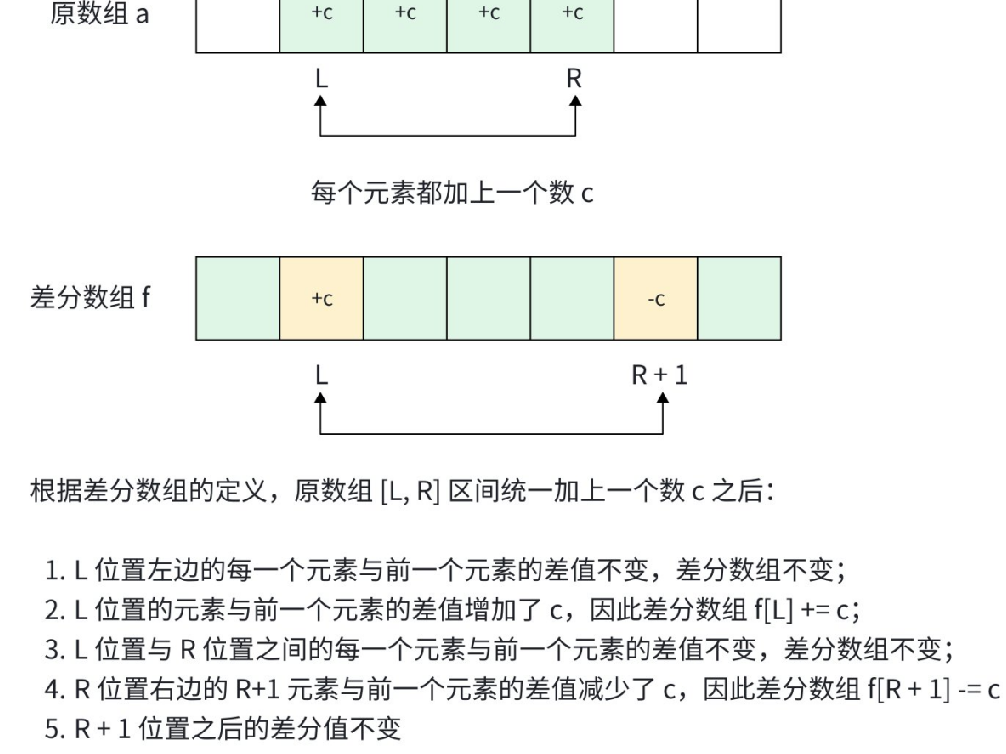
还原经过 q 次询问之后的 a 数组：对差分数组做⼀次「前缀和」，就可以还原出原数组

由差分数组的定义得：原数组a 中的每⼀项：

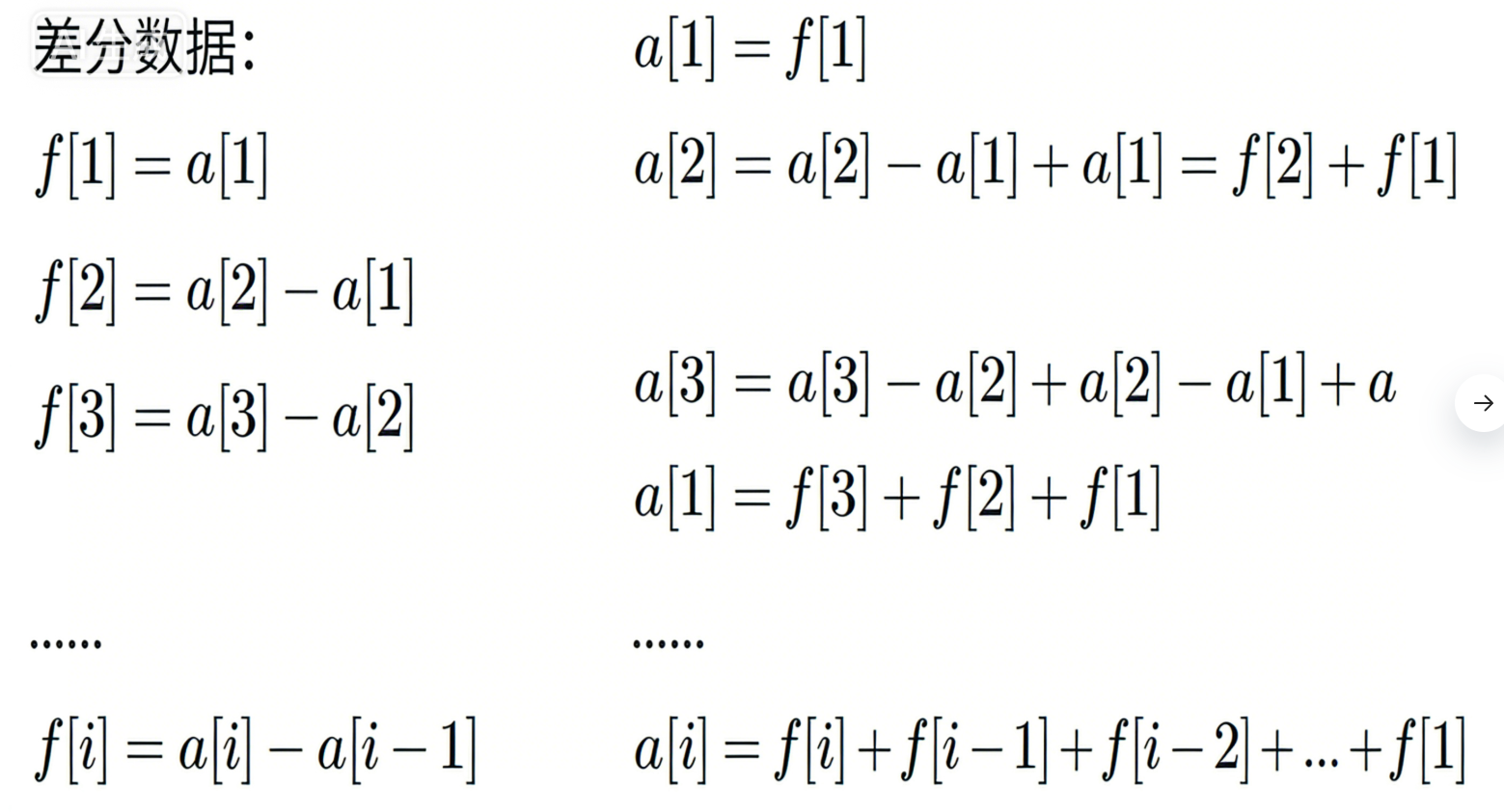
#include <iostream>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
int n, m;
LL f[N]; // 差分数组 
int main()
{
 cin >> n >> m;
 // 利⽤差分数组的性质，创建差分数组 
 for(int i = 1; i <= n; i++)
 {
 LL x; cin >> x;
 f[i] += x;
 f[i + 1] -= x;
 } 
 
 // 处理 m 次修改操作 
 while(m--)
 {
 LL l, r, k; cin >> l >> r >> k;
 f[l] += k; f[r + 1] -= k;
 }
 
 // 还原出原始的数组 
 for(int i = 1; i <= n; i++)
 {
 f[i] = f[i - 1] + f[i];
 cout << f[i] << " ";
 }
 
 return 0;
}

⚠️ 易错点提示

差分数组大小要 n+2，防止 r+1 越界；
二维差分四个角都要更新。

六、双指针：滑动窗口优化暴力

双指针算法有时候也叫尺取法或者滑动窗⼝，是⼀种优化暴⼒枚举策略的⼿段：

原理讲解

当暴力枚举中两个指针都不回退，可用双指针将 O(n²) 优化至 O(n)。

当我们发现在两层 for 循环的暴⼒枚举过程中，两个指针是可以不回退的，此时我们就可以利⽤两个指针不回退的性质来优化时间复杂度。

因为双指针算法中，两个指针是朝着同⼀个⽅向移动的，因此也叫做同向双指针。

注意：希望⼤家在学习该算法的时候，不要只是去记忆模板，⼀定要学会如何从暴⼒解法优化成双指

📌 经典题型

题目	目标	判断条件
唯一的雪花	最长无重复子串	mp[a[right]] > 1
逛画展	最短包含所有画家的区间	kind == m
丢手绢（环形）	最远距离	2*k >= sum

模版：

// 通用滑动窗口模板
while (right < n) {
    // 进窗口
    if (满足条件) {
        while (窗口不合法) {
            // 出窗口
            left++;
        }
        // 更新答案
    }
    right++;
}

⚠️ 易错点提示

环形问题可断环为链（但本题用双指针更优）；
出窗口时注意 kind 计数更新。

七、二分：从查找 → 答案

原理讲解

二段性 = 答案一侧全满足，另一侧全不满足。

二分查找（左/右端点模板）

// 左端点（>=x 的第一个）
while (l < r) {
    int mid = (l + r) / 2;
    if (check(mid)) r = mid;
    else l = mid + 1;
}

// 右端点（<=x 的最后一个）
while (l < r) {
    int mid = (l + r + 1) / 2;
    if (check(mid)) l = mid;
    else r = mid - 1;
}

二分答案：最大值最小 / 最小值最大

题目	二分对象	check函数
木材加工	切割长度L	总段数 >= k
砍树	锯片高度H	木材总量 >= M
跳石头	最短跳跃距离	移走石头数 <= M

⚠️ 易错点提示

二分答案时，check 函数要正确模拟；
注意 mid 是否 +1，防止死循环；
边界情况（如全满足/全不满足）要特判。

总结：基础算法学习路径图

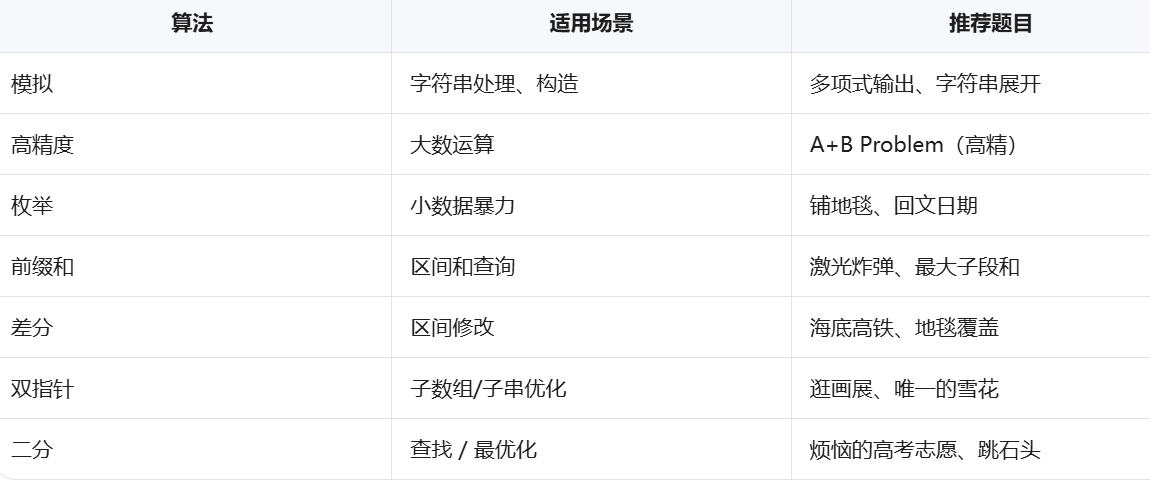
刷题建议

先掌握模板：前缀和、差分、二分模板必须手写熟练；
重点练“转化”：如“砍树”→二分高度，“跳石头”→二分距离；
OJ 推荐：
- 洛谷：搜索“基础算法”标签；
- 牛客：《算法竞赛入门课》前缀和/差分章节；
- LeetCode：78（子集）、209（最小窗口）。

记住：基础不牢，地动山摇。把这些“简单题”做到滴水不漏，你离 ACM 区域赛/大厂 offer 就不远了！

思考题：

1. 为什么高精度乘法要“先无进位相乘，再统一进位”？
2. 二分答案中，如何判断一个问题是否具有“二段性”？
欢迎在评论区留言讨论！

8 条评论

给东岸来杯冷咖啡 2025.12.28
二分答案中，如何判断一个问题是否具有“二段性”？一个问题具有“二段性”是指存在一个分界点，使得解空间能被分成两段：一段全部满足条件（如可行），另一段全不满足。判断方法是：检查是否对于某个值 x，满足条件的解在 x 一侧单调成立（例如所有大于 x 的值都可行，小于都不可行），从而可以通过二分快速找到分界点。
- 给东岸来杯冷咖啡回复给东岸来杯冷咖啡 2025.12.28
  答案仅供参考[face]emoji:005.png[/face][face]emoji:005.png[/face]

给东岸来杯冷咖啡 2025.12.28
为什么高精度乘法要“先无进位相乘，再统一进位”？这样做可以简化计算过程：先逐位相乘并暂存所有中间结果（忽略进位），最后再一次性处理所有进位。这能提高效率，避免每一步都处理进位带来的复杂度，使算法更易实现和调试。
- 给东岸来杯冷咖啡回复给东岸来杯冷咖啡 2025.12.28
  答案在这里[face]emoji:005.png[/face][face]emoji:005.png[/face]