排序算法优劣势总结

1 插入类

1.1 直接插入排序

思想：将数组分为有序区和无序区，有序区开始只有一个元素，从第二个元素（无序区的第一个元素）arr[i]开始，由于arr[1]-arr[i-1]已经有序，所以从后面往前判断，若大于当前值r[j]），则将r[j]-r[i-1]向后挪一位，随后插入。

空间复杂度：O(1)

时间复杂度：O(n^2)

优势：小规模输入、有序

劣势：刚好反序的、大规模输入

稳定性：稳定

1.2 折半插入排序

思想：在直接插入的基础上，在r[1]-r[i-1]中确定r[i]的插入顺序使用二分查找。

空间复杂度：O(1)

时间复杂度：O(n^2)（虽然优化了查找的时间效率，但移位次数没有变化，所以仍为n^2）

优势：规模比较大的输入

劣势：相对于直接插入劣势基本没有

稳定性：稳定

1.3 希尔排序

思想：将数组分隔为若干个子序列（由相隔某个“增量”的元素组成的），分别对每个子序列进行直接插入排序，然后缩小增量再进行排序，待整个数组基本有序再进行一次整体的直接插入排序。（子序列的说明：比如5 4 8 9 2 6，增量为3，子序列分别为5 9、4 2、8 6）。

空间复杂度：O(1)

时间复杂度：需要根据增量的选择来看，通常比O(n^2)要好

优势：最坏情况下和平均情况差不多，中小规模输入

劣势：大规模输入（比一般的O(n^2)要好）

稳定性：不稳定

引申：关于希尔排序稳定性的思索：使用希尔排序后相同元素的相对位置为什么可能发生改变，希尔排序不是最后也全体直接插入排序了一次吗？

希尔排序最后需要对全体数组成员进行直接插入排序，但是这次排序不会改变相同元素的相对位置，因为以前对各个子序列进行的直接插入排序可能影响了这些相同元素的相对位置，而且最后一次整体插入排序不改变相同元素的相对位置，所以希尔排序是不稳定的。

2 交换类排序

2.1 冒泡排序

思想：比较相邻两个元素的大小，若逆序则交换位置。

空间复杂度：O(1)

时间复杂度：O(n^2)

优势：正序输入

劣势：对于最小值很后置的输入

稳定性：稳定

引申：冒泡排序的优化？

        flag = 1;
        for (i=0; i<r.length && flag; i++){
            
            flag = 0;
            for (j=0; j<r.length-i-1; j++){
                if(r[j] > r[j+1]){
                    t = r[j] ;
                    r[j] = r[j+1] ;
                    r[j+1] = t ;
                    flag = 1;
                }
            }
        }

当数组正序后，交换元素的代码不用执行，所以flag = 0，直接返回就可以了。

2.2 快速排序

思想：从待排序列中任意选择一个元素，以该元素作为“枢轴”，凡小于枢轴的元素均移动至枢轴之前，凡大于枢轴的元素均移动至枢轴之后。

空间复杂度：O(logn)

时间复杂度：O(nlogn)

优势：速度快

劣势：若枢轴选择不好，每次都是最大或最小，剩下的元素就全被分配到一个序列中，另一个序列为空，此时效率最差。

稳定性：不稳定。

3 选择类排序

3.1 简单选择排序

思想：从arr[1]开始，将序列a[2-n]后面的元素中的最小值和arr[1]交换，在对arr[2]执行同样的操作......

空间复杂度：O(1)

时间复杂度：O(n^2)

优势：可以提前知道交换的次数、相对于冒泡排序交换次数降低

劣势：比较次数略多

稳定性：不稳定。

3.2 树形选择排序

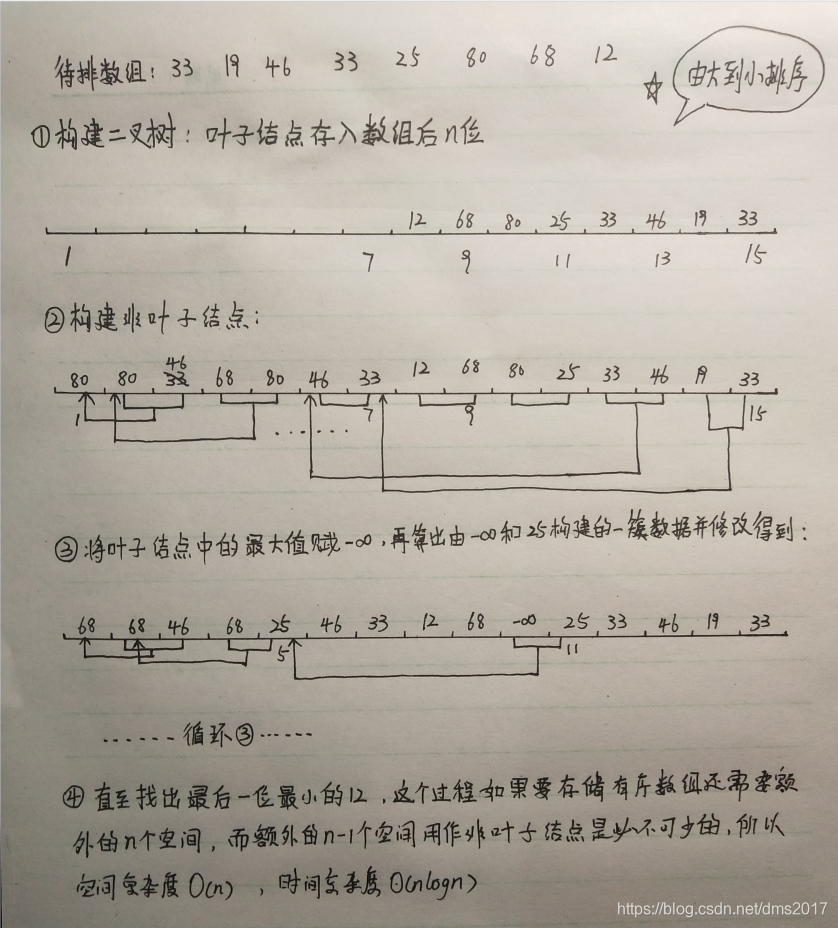
思想：将arr[n]作为一个完全二叉树的所有叶子结点，将它们相邻元素两两进行比较，选出较小者，再对这些较小者两两比较选出更小者......直到选出最小的元素。

以下是结合代码实现的树形选择排序的过程：

    public int[] TreeSelectionSort(int[] r)
    {
        int MinValue = -10000 ;              //极值
        int[]tree = new int[r.length * 4] ;  //树的大小(非真实长度)
        int baseSize = 1 ;                   //求树的长度用的辅助变量
        int n = r.length ;                   //待排数的个数
        int max ;                            //记录树结构中最大值的变量
        int maxIndex ;                       //记录树结构中最大值的下标变化的变量
        int treeSize ;                       //树的真实长度
 
        int i ;
        while (baseSize < n) {    //求叶子节点为n的完全二叉树的节点个数
            baseSize *= 2 ;
        }
        treeSize = baseSize * 2 - 1 ;
 
        //从后往前存放叶子节点
        for (i = 0; i < n; i++) {
            tree[treeSize - i] = r[i] ;
        }
 
        //此时i=n，给剩余的一个叶子节点赋一个空值
        for (; i < baseSize; i++) {
            tree[treeSize - i] = MinValue ;
        }
 
        //构造树的非叶子节点,0位数组不用
        for (i = treeSize; i > 1; i -= 2) {
            tree[i / 2] = (tree[i] > tree[i - 1] ? tree[i] : tree[i - 1]) ;
        }
 
        n -= 1 ;
        while (n != -1)
        {
            max = tree[1] ;
            r[n--] = max ;
            maxIndex = treeSize ;
 
            //寻找叶子节点中最大值的数组下标
            while (tree[maxIndex] != max) {
                maxIndex-- ;
            }
            tree[maxIndex] = MinValue ;      //赋极小值
 
            while (maxIndex > 1) {
 
                if (maxIndex % 2 == 0) {      //是左节点，为啥要分左右？因为maxIndex奇偶性不确定
                    tree[maxIndex / 2] = (tree[maxIndex] > tree[maxIndex + 1] ? tree[maxIndex] : tree[maxIndex + 1]) ;
                }
                else {
                    tree[maxIndex / 2] = (tree[maxIndex] > tree[maxIndex - 1] ? tree[maxIndex] : tree[maxIndex - 1]) ;
                }
                maxIndex /= 2 ;
            }
        }
        return r ;
    }

空间复杂度：O(n)

时间复杂度：O(n^2)

优势：明显降低比较次数、排序性能稳定（针对不同的输入的效果大致相同）

劣势：占用较多辅助空间

稳定性：稳定

3.3 堆排序

思想：

空间复杂度：

时间复杂度：

优势：

劣势：

稳定性：