在工业控制领域，PID 控制器因结构简单、鲁棒性强、易于实现等优点，被广泛应用于温度、压力、流量等过程控制场景。但传统 PID 参数整定（如经验法、Ziegler-Nichols 法）往往依赖工程师经验，难以获得最优控制效果。本文将通过水温恒定控制实验，对比常规 PID 与粒子群算法（PSO）优化 PID 的控制性能，带大家深入理解智能优化算法在 PID 参数整定中的应用。
一、实验背景与目标
1.1 控制场景
以水温恒定控制为研究对象：将初始温度 25℃的水加热至 80℃并保持恒定，模拟热水器、工业反应釜等实际温度控制场景。
1.2 被控对象模型
水温系统属于典型的一阶惯性 + 纯滞后系统（温度变化存在惯性，加热指令到温度响应存在延迟），数学模型参数如下：
- 系统增益 K = 0.8（加热效率，输出温度变化与输入控制量的比值）
- 时间常数 T = 15s（系统惯性，温度达到稳态值 63.2% 所需时间）
- 纯滞后时间
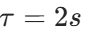（响应延迟，加热指令发出后，温度开始变化的延迟时间）
1.3 实验目标
- 用粒子群算法（PSO）优化 PID 控制器的 3 个核心参数（比例系数Kp、积分系数Ki、微分系数Kd）；
- 对比优化 PID 与常规手动整定 PID 的控制性能（超调量、调节时间、稳态误差）；
- 通过 Matlab 仿真验证 PSO 优化 PID 的优越性。
二、核心算法原理
2.1 PID 控制原理
PID 控制器通过比例（P）、积分（I）、微分（D） 三个环节的组合，根据 “偏差（目标值 - 实际值）” 动态调整控制量，公式如下：
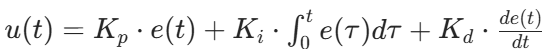
- 比例环节（P）：快速响应偏差，增大\(K_p\)可加快响应，但易导致超调；
- 积分环节（I）：消除稳态误差，增大\(K_i\)可减小静差，但易导致震荡；
- 微分环节（D）：预测偏差变化趋势，增大\(K_d\)可抑制超调，但易受噪声干扰。
PID 参数的整定本质是寻找一组\([K_p, K_i, K_d]\)，使控制性能（如超调量小、调节时间短、稳态误差小）最优。
2.2 粒子群算法（PSO）原理
PSO 是一种基于群体智能的优化算法，模拟鸟群觅食行为：每个 “粒子” 代表一个待优化的解（本文中即一组 PID 参数），通过跟踪 “个体最优（pbest）” 和 “全局最优（gbest）” 动态更新位置（参数值），最终收敛到最优解。
2.2.1 PSO 核心公式
- 速度更新（决定粒子下一步移动的方向和步长）
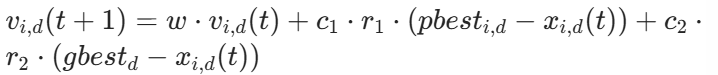
- 位置更新（更新粒子代表的参数值）：
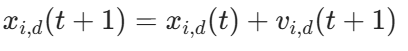
2.2.2 PSO 参数说明
- w：惯性权重（控制粒子保持原速度的倾向，本文取 0.8，前期大权重探索、后期小权重收敛）；
- c1, c2：学习因子（c1是个体学习因子，c2是群体学习因子，本文分别取 1.5、2.0）；
- r1, r2：[0,1] 随机数（增加搜索随机性，避免陷入局部最优）；
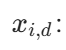第 i 个粒子在第 d 维的位置（本文 d=3，对应\(K_p, K_i, K_d\)）；
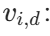第 i 个粒子在第 d 维的速度。
2.2.3 适应度函数（优化目标）
本文采用ITAE 指标（时间加权绝对误差积分）作为适应度函数，ITAE 越小，控制性能越好：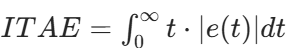
ITAE 对后期误差的惩罚更重，能有效抑制超调和缩短调节时间，适合温度等慢响应系统。
三、Matlab 仿真实现（完整代码 + 解析）
3.1 代码整体结构
实验代码分为 6 个核心模块：
- 系统参数设置（目标温度、被控对象模型、常规 PID 参数）；
- PSO 参数设置与粒子初始化；
- PSO 优化 PID 参数；
- 优化 PID 与常规 PID 仿真对比；
- 控制性能指标计算；
- 结果可视化与输出。
3.2 完整代码:
%% 粒子群算法优化PID控制实验
% 控制目标：水温恒定在80℃
% 对比：优化PID vs 常规PID
% 清除工作空间、命令窗口和关闭所有图形窗口
clc; % 清除命令窗口
clear; % 清除工作空间变量
close all; % 关闭所有图形窗口
%% ==================== 系统参数设置 ====================
target_temp = 80; % 目标温度(℃)
initial_temp = 25; % 初始温度(℃)
sim_time = 100; % 仿真总时间(s)
dt = 0.1; % 仿真步长/采样时间(s)
t = 0:dt:sim_time; % 创建时间向量(0到100s，步长0.1s)
n_steps = length(t); % 总仿真步数
% 被控对象模型参数 (水温系统一阶惯性加纯滞后模型)
K = 0.8; % 系统增益(加热效率)
T = 15; % 时间常数(s)(系统惯性)
tau = 2; % 纯滞后时间(s)(温度响应延迟)
delay_steps = round(tau/dt); % 将滞后时间转换为仿真步数（20步）
% 常规PID参数（手动整定值 - 作为对比基准）
manual_Kp = 8.5; % 比例系数
manual_Ki = 0.05; % 积分系数
manual_Kd = 12; % 微分系数
%% ==================== 粒子群算法参数设置 ====================
n_particles = 30; % 粒子群规模（粒子数量，30个粒子平衡搜索效率与精度）
max_iter = 50; % 最大迭代次数（50次迭代足够收敛）
w = 0.8; % 初始惯性权重
c1 = 1.5; % 个体学习因子
c2 = 2.0; % 群体学习因子
% PID参数搜索范围（根据水温系统特性设定，避免参数过偏）
Kp_range = [5, 20]; % Kp取值范围（过小响应慢，过大超调大）
Ki_range = [0.01, 0.2]; % Ki取值范围（过小静差大，过大震荡）
Kd_range = [5, 30]; % Kd取值范围（过小抑制超调弱，过大抗扰差）
% 初始化粒子群（每个粒子代表一组PID参数 [Kp, Ki, Kd]）
particles = struct('position', [], 'velocity', [], 'pbest_pos', [], 'pbest_fit', []);
for i = 1:n_particles
% 1. 随机生成PID参数（在设定范围内均匀分布）
Kp = Kp_range(1) + rand() * (Kp_range(2) - Kp_range(1));
Ki = Ki_range(1) + rand() * (Ki_range(2) - Ki_range(1));
Kd = Kd_range(1) + rand() * (Kd_range(2) - Kd_range(1));
particles(i).position = [Kp, Ki, Kd];
% 2. 初始化粒子速度（初始速度设为参数范围的10%，避免初始步长过大）
vel_Kp = 0.1 * (Kp_range(2) - Kp_range(1)) * (rand() - 0.5);
vel_Ki = 0.1 * (Ki_range(2) - Ki_range(1)) * (rand() - 0.5);
vel_Kd = 0.1 * (Kd_range(2) - Kd_range(1)) * (rand() - 0.5);
particles(i).velocity = [vel_Kp, vel_Ki, vel_Kd];
% 3. 初始化个体最优位置为当前位置
particles(i).pbest_pos = particles(i).position;
% 4. 计算初始个体最优适应度（调用系统仿真和ITAE计算函数）
[~, error] = simulate_system(particles(i).position, target_temp, initial_temp, t, dt, K, T, delay_steps);
particles(i).pbest_fit = calculate_ITAE(error, t);
end
% 初始化全局最优位置和适应度（从个体最优中筛选）
[gbest_fit, gbest_idx] = min([particles.pbest_fit]);
gbest_position = particles(gbest_idx).pbest_pos;
%% ==================== PSO优化过程 ====================
fitness_history = zeros(1, max_iter); % 存储每次迭代的最优适应度值
% 主循环：执行PSO优化迭代
for iter = 1:max_iter
% 1. 更新每个粒子的速度和位置
for i = 1:n_particles
% 速度更新（按PSO公式计算）
r1 = rand(1, 3); % 3维随机数（对应Kp, Ki, Kd）
r2 = rand(1, 3);
particles(i).velocity = w * particles(i).velocity ...
+ c1 * r1 .* (particles(i).pbest_pos - particles(i).position) ...
+ c2 * r2 .* (gbest_position - particles(i).position);
% 位置更新（避免参数超出设定范围，做边界限制）
particles(i).position = particles(i).position + particles(i).velocity;
particles(i).position(1) = max(Kp_range(1), min(Kp_range(2), particles(i).position(1))); % Kp边界
particles(i).position(2) = max(Ki_range(1), min(Ki_range(2), particles(i).position(2))); % Ki边界
particles(i).position(3) = max(Kd_range(1), min(Kd_range(2), particles(i).position(3))); % Kd边界
% 2. 计算当前粒子的适应度（ITAE）
[~, error] = simulate_system(particles(i).position, target_temp, initial_temp, t, dt, K, T, delay_steps);
current_fit = calculate_ITAE(error, t);
% 3. 更新个体最优（若当前适应度更优）
if current_fit < particles(i).pbest_fit
particles(i).pbest_fit = current_fit;
particles(i).pbest_pos = particles(i).position;
end
end
% 4. 更新全局最优（从所有个体最优中筛选）
current_pbest_fits = [particles.pbest_fit];
[current_gbest_fit, current_gbest_idx] = min(current_pbest_fits);
if current_gbest_fit < gbest_fit
gbest_fit = current_gbest_fit;
gbest_position = particles(current_gbest_idx).pbest_pos;
end
% 记录当前迭代的最优适应度
fitness_history(iter) = gbest_fit;
% （可选）打印迭代过程（查看优化进度）
fprintf('迭代次数：%d / %d，当前最优ITAE：%.4f，最优PID：[%.2f, %.4f, %.2f]\n', ...
iter, max_iter, gbest_fit, gbest_position(1), gbest_position(2), gbest_position(3));
end
% 提取优化后的PID参数
opt_Kp = gbest_position(1); % 优化后的比例系数
opt_Ki = gbest_position(2); % 优化后的积分系数
opt_Kd = gbest_position(3); % 优化后的微分系数
%% ==================== 仿真比较 ====================
% 使用优化后的PID参数进行温度控制仿真
[opt_temp, opt_error] = simulate_system([opt_Kp, opt_Ki, opt_Kd], target_temp, initial_temp, t, dt, K, T, delay_steps);
% 使用手动整定的PID参数进行温度控制仿真
[manual_temp, manual_error] = simulate_system([manual_Kp, manual_Ki, manual_Kd], target_temp, initial_temp, t, dt, K, T, delay_steps);
%% ==================== 性能指标计算 ====================
% 计算优化PID的性能指标（超调量、调节时间、稳态误差）
[opt_overshoot, opt_settling_time] = calculate_performance(opt_temp, target_temp, t, 5); % 5%误差带
opt_steady_error = abs(target_temp - opt_temp(end)); % 稳态误差=目标值-最终温度
% 计算常规PID的性能指标
[manual_overshoot, manual_settling_time] = calculate_performance(manual_temp, target_temp, t, 5);
manual_steady_error = abs(target_temp - manual_temp(end));
%% ==================== 结果可视化 ====================
% 创建新图形窗口
figure('Position', [100, 100, 1000, 600]); % 设置窗口位置和大小
% 绘制温度响应曲线对比
plot(t, opt_temp, 'b-', 'LineWidth', 1.5); % 优化PID温度曲线(蓝色实线)
hold on; % 保持图形
plot(t, manual_temp, 'r--', 'LineWidth', 1.5); % 常规PID温度曲线(红色虚线)
yline(target_temp, 'k--', 'LineWidth', 1.5); % 目标温度参考线(黑色虚线)
title('水温控制响应曲线对比（目标80℃）', 'FontSize', 14); % 标题
xlabel('时间 (s)', 'FontSize', 12); % X轴标签
ylabel('温度 (℃)', 'FontSize', 12); % Y轴标签
legend(['PSO优化PID (Kp=', num2str(opt_Kp, '%.2f'), ', Ki=', num2str(opt_Ki, '%.4f'), ... % 图例
', Kd=', num2str(opt_Kd, '%.2f'), ')'], ...
['常规手动PID (Kp=', num2str(manual_Kp, '%.2f'), ', Ki=', num2str(manual_Ki, '%.4f'), ...
', Kd=', num2str(manual_Kd, '%.2f'), ')'], '目标温度', 'Location', 'southeast', 'FontSize', 10);
grid on; % 显示网格
hold off;
% （可选）绘制适应度变化曲线（查看PSO收敛过程）
figure('Position', [200, 200, 800, 400]);
plot(1:max_iter, fitness_history, 'g-', 'LineWidth', 1.5);
title('PSO优化过程：最优适应度(ITAE)变化', 'FontSize', 14);
xlabel('迭代次数', 'FontSize', 12);
ylabel('ITAE值（越小越好）', 'FontSize', 12);
grid on;
% 控制台输出性能指标对比
fprintf('\n===== 水温控制性能指标对比（目标80℃） =====\n');
fprintf(' | 超调量(℃) | 调节时间(s) | 稳态误差(℃)\n');
fprintf('优化PID | %6.3f | %6.2f | %6.3f\n', ...
opt_overshoot, opt_settling_time, opt_steady_error);
fprintf('常规PID | %6.3f | %6.2f | %6.3f\n', ...
manual_overshoot, manual_settling_time, manual_steady_error);
%% ==================== 辅助函数 ====================
%% 系统仿真函数：实现水温系统（一阶惯性+纯滞后）与PID控制
% 输入：PID参数、目标温度、初始温度、时间向量、系统模型参数
% 输出：温度响应曲线、误差曲线
function [temp, error] = simulate_system(pid_params, target, init_temp, t, dt, K
扫一扫
105
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
