剑指 Offer 33. 二叉搜索树的后序遍历序列（中等）

思路：

此题只是判断数组是否符合条件，只需要判断数组即可，不用返回数组

方法一：深度优先搜索（递归）

方法二：单调栈

 

代码：

方法一：

class Solution {
    public boolean verifyPostorder(int[] postorder) {
		return dfs(postorder,0,postorder.length-1);
		
    }
	
	private boolean dfs(
				int[] postorder,
				int i,
				int j
	){
		//注意边界，是"="
		if(i>=j){
			return true;
		} 
		
		int p=i;
		while(postorder[p]<postorder[j]){
			p++;
		}
		
		int m=p;
		while(postorder[p]>postorder[j]){
			p++;
		}
		
		//第一个：是i而不是0
		//第二个：根不是j，所以是j-1
		return p==j&&dfs(postorder,i,m-1)&&dfs(postorder,m,j-1);
	}
}

方法二：

class Solution {
    public boolean verifyPostorder(int[] postorder) {
		Deque<Integer> stack=new ArrayDeque<>();
		int root=Integer.MAX_VALUE;
		for(int i=postorder.length-1;i>=0;i--){
			if(postorder[i]>root){
				return false;
			}
			while(!stack.isEmpty()&&postorder[i]<stack.peekLast()){
				root=stack.removeLast();
			}
			stack.addLast(postorder[i]);
		}
		return true;
	}
}

 

分解：

1）方法一：

    i）注意边界，是"i>=j"而不是"i>j"

    ii）递归时，有三个项：

         1.判断p==j，表明每次都搜寻完了

         2.左边递归（i,m-1），注意是i而不是0

         3.右边递归（m,j-1），注意是j-1而不是j

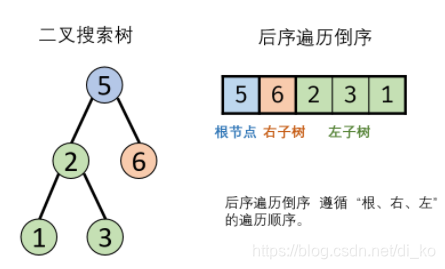
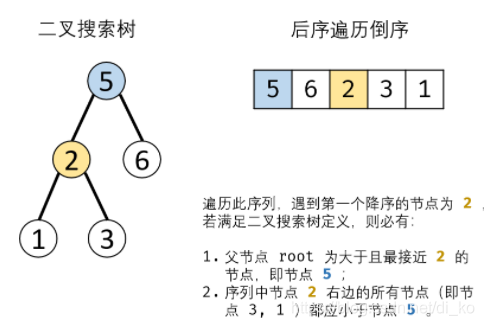
整个过程是：最后一个是根节点，根节点左边都小于根节点，根节点右边都大于根节点

                      利用一个变量标记左右节点的转换点

 

2）方法二：

利用后序遍历倒序和一个单调栈。

注意每次while循环体都是把一整个当前情况的树节点都弹出，使得单调栈能用于下一个情况

 

复杂度分析：

方法一：

    i）时间复杂度：O（N^2） 每次递归的时间复杂度都是O（N），最差情况下每次都要搜索到最后一个

    ii）空间复杂度：O（N） 最差情况下是一个链表，递归的深度为节点数N

 

方法二：

    i）时间复杂度：O（N） 每个节点都加入、弹出单调栈一次

    ii）空间复杂度：O（N） 额外空间是一个单调栈