理论知识.区间问题.区间合并

区间问题

区间问题的引入

数学上，用两个数字可以确定数轴上的一个区间，较小的数字叫做区间的左端点，也叫区间起点，较大的数字叫做区间的右端点，也叫区间终点。

在算法竞赛中，很多题目是以区间为单位去进行标记和运算的。例如，学校门口种了很多树，从坐标 0 到坐标 L 之间，整数位置都都一棵树。现在进行多次拔树操作，每次操作是把从位置 a 到 位置 b 的树拔掉（如果那个位置有树的话），进行了若干轮操作之后，问在哪些地方还有树（没有拔掉）。在这个问题中，就是以区间为单位的去计算的。用笨方法做，就是每一次拔树操作就写一个 for 循环，但是这样子的执行效率很低，很容易超时。

上述的 “拔树问题” 中，可以对多次操作记录成区间，然后 按顺序的去合并区间 ，合并不成功的时候意味着两个区间之间有一些“缝隙”，这些缝隙就是最终还保留着树的地方，我们对缝隙进行计算就可以得到正确的答案了。区间合并的过程中因为只需要对前项后项的两个端点进行比较，所以少了一个 for 循环，运行效率能大幅度提高。

区间的定义

可以用一个结构体去描述区间变量，区间只有两个重要因素：区间的左端点 和 区间的右端点，所以，定义结构体的时候就需要包含这两个信息（根据不同的题目，有时候可以扩展出新的结构体成员变量）

struct Zone
{
	int l,r;
};

Copy

两个区间的关系

如果没有任何的附加条件，两个区间 zone1 [l_1l1​,r_1r1​] 和 zone2 [l_2l2​,r_2r2​] 之间存在的关系是多种多样的。存在的情况越多，就越难写程序，可以理解到的是 if 语句的分支就会很多，一个小小的疏忽都会导致错误。所以，非常有必要对区间进行排序，然后再来做区间运算。常见的区间排序方法有两种：

1. 按左端点从小到大排序

bool cmp1(Zone i,Zone j)
{
	return i.l<j.l||(i.l==j.l&&i.r<j.r);
}

Copy

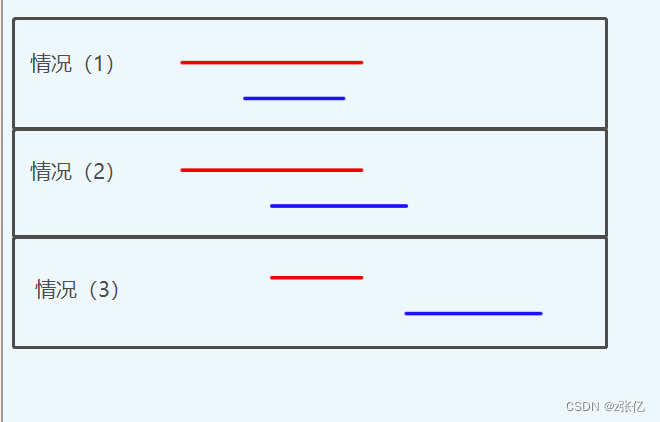
按照左端点从小到大排序之后，两个区间之间的关系存在上图所描绘的 3 种情况，红色线条代表 前项，蓝色线条代表后项:

• 情况(1): 前项包含后项
• 情况(2): 前项和后项有重叠
• 情况(3): 前项和后项分离

1. 按有端点从小到大排序

bool cmp2(Zone i,Zone j)
{
	return i.r<j.r||(i.r==j.r&&i.l<j.l);
}

Copy

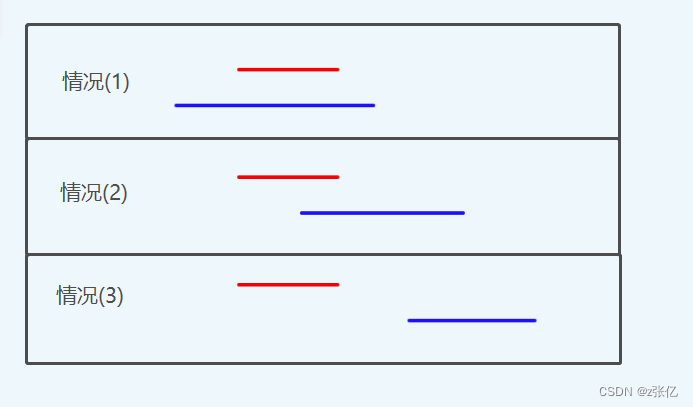
按照右端点从小到大排序之后，两个区间之间的关系存在上图所描绘的 3 种情况，红色线条代表 前项，蓝色线条代表后项:

• 情况(1): 前项包含后项
• 情况(2): 前项和后项有重叠
• 情况(3): 前项和后项分离

不同的排序方法解决不同类型的问题

不同的题目，需要按照不同的方式排序。下面举几个例子加以说明：

1. P1303. 校门外的树

题目问的是最后剩余的树的数量，可以按照左端点从小到大排序，然后进行区间合并。3 种情况（见上图图例）中，第(1) 种和第 (2) 种情况都能把两个区间（前项和后项）合并成功，第 (3) 种情况会出现缝隙。解题的关键就是关注和统计缝隙里包含的整数。

1. NH.2019.模拟.03.兴奋的桐桐

题目问的是总共兴奋了多少天，每一次获奖都产生了一个兴奋期的区间，把这些区间合并起来，合并的过程关注区间内包含的整数有多少个。一般来说，是前项和后项合并失败的时候取统计前项区间包含了多少天，然后后项作为了一个新的区间继续和更后面的区间合并。这条题，按照前项或者后项排序都可以。

1. P1160. 活动选择

所有的活动都要在礼堂进行，礼堂同一个时间不能同时举办两个活动，所以，最终选择的活动在时间上是彼此不重叠的。而题目希望尽可能安排多一些活动，要认真审题，题目关心的是活动的数量，而不是活动的时间长度，再长时间的 1 个活动也只是算 1 个活动。

这种题目，要用右端点从小到大排序。我们用的是贪心算法，我们一个个活动去选，选第一个活动的准则应该是：所有活动中结束时间最早的那一个，这样子就可以早一些让礼堂空闲出来安排下一个活动；然后选第二个活动也是同样的法则，尽量让礼堂早点空闲。而让礼让早点空闲下来的就是右端点小一点的区间，因此按照右端点从小到大排序是合适的。

理解了上面的思路之后，也可以换一个思路：按照左端点从大到小排序，然后先选最后一个能安排的活动，自然就是选左端点最大的那一个区间了，目的是让礼堂前面的空闲时间尽量长一些，好安排前面的活动；然后再从剩余的活动里面选尽量晚开始的，一直循环下去。所以，不同的排序方法也是可以的，但是最终程序的写法也不一样