【洛谷P4284】【7.19模拟赛T4】概率充电器【期望DP】

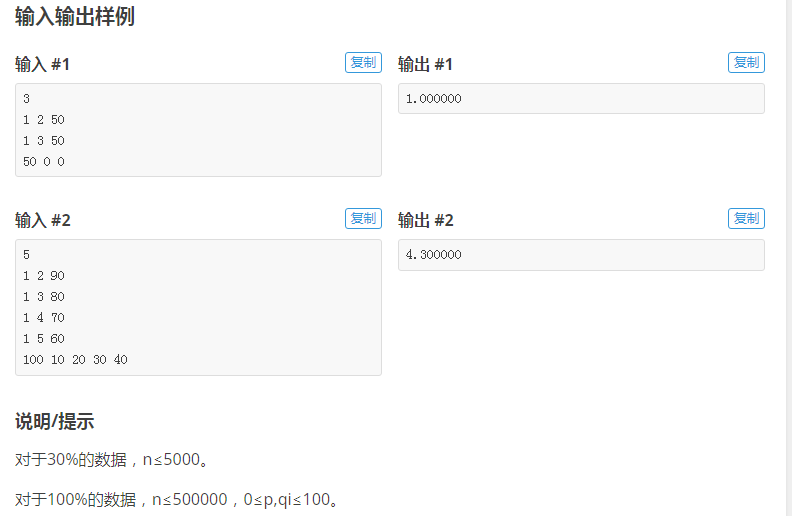
题目链接：概率充电器

分析

需要把期望变成每个点对答案的贡献，被点亮为1，没点亮为0.
所以就只跟概率有关了。

设$f[x]$表示x这个点不连通的概率
考虑x的儿子对它的贡献$f[x]=(1-q[x])\ast \prod (1-w+f[y]\ast w)$其中y为x的儿子，w为边连通的概率。
现在考虑y的父亲x对y的贡献，我们设s为x除去y这个点连通的概率$s=1-f[x]/(1-w+f[y]\ast w)$。于是$f[v]\ast =1-s\ast w$
两遍DFS算出$f$数组

最后求和$1-f[i]$。

上代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

struct lwx
{
	int to,next;
	double w;
}e[1000010];

int n;
int tot,hd[500005];
double ans,f[500005],a[500005];

void add(int x,int y,double w)
{
	e[++tot]=(lwx){y,hd[x],w};
	hd[x]=tot;
}

void dfs1(int x,int fa)
{
	f[x]=1-a[x];
	for(int i=hd[x];i>0;i=e[i].next)
	{
		int y=e[i].to;
		if(y!=fa)
		{
			dfs1(y,x);
			f[x]*=1-e[i].w+e[i].w*f[y];
		}
	}
	return;
}

void dfs2(int x,int fa)
{
	for(int i=hd[x];i>0;i=e[i].next)
	{
		int y=e[i].to;
		if(y!=fa)
		{
			double s=1-f[x]/(1-(1-f[y])*e[i].w);
			if(s>1e-9&&f[y]>1e-9)
			{
				f[y]*=1-s*e[i].w;
			}
			dfs2(y,x);
		}
	}
	return;
}

int main()
{
//	freopen("charger.in","r",stdin);
//	freopen("charger.out","w",stdout);
	cin>>n;
	for(int i=1;i<=n-1;i++)
	{
		int a,b,p;
		cin>>a>>b>>p;
		double x=1.0*p/100;
		add(a,b,x);
		add(b,a,x);
	}
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		a[i]=x*1.0/100;
	}
	dfs1(1,0);
	dfs2(1,0);
	for(int i=1;i<=n;i++)
	{
		ans+=1-f[i];
	}
	printf("%.6lf",ans);
	return 0;
}