二叉堆
二叉堆就是一个完全二叉树。几乎在所有需要用到优先队列的时候,使用它就完事了。只需要一个数组,完美的插入,删除,查询时间复杂度。但是残念,二叉堆的合并至少需要o(n)的复杂度。
D-堆
D堆就是一个完全d叉树。所以,d堆会比二叉堆浅的多。
左式堆
Clark Allan Crane,1972年发明。叫这个名字地原因就是这个树左边比右边高。左式堆不是理想平衡的,而是实际上非常趋向于不平衡的。
零路径长:从节点X到一个没有两个子节点的(有一个子节点或没有子节点)节点的最短距离
左式堆首先是一个二叉查找树。附加一个条件
要求任一节点的左子节点零路径长大于等于右子节点的零路径长
左式堆的合并过程
第一步,符合堆的原则进行合并。
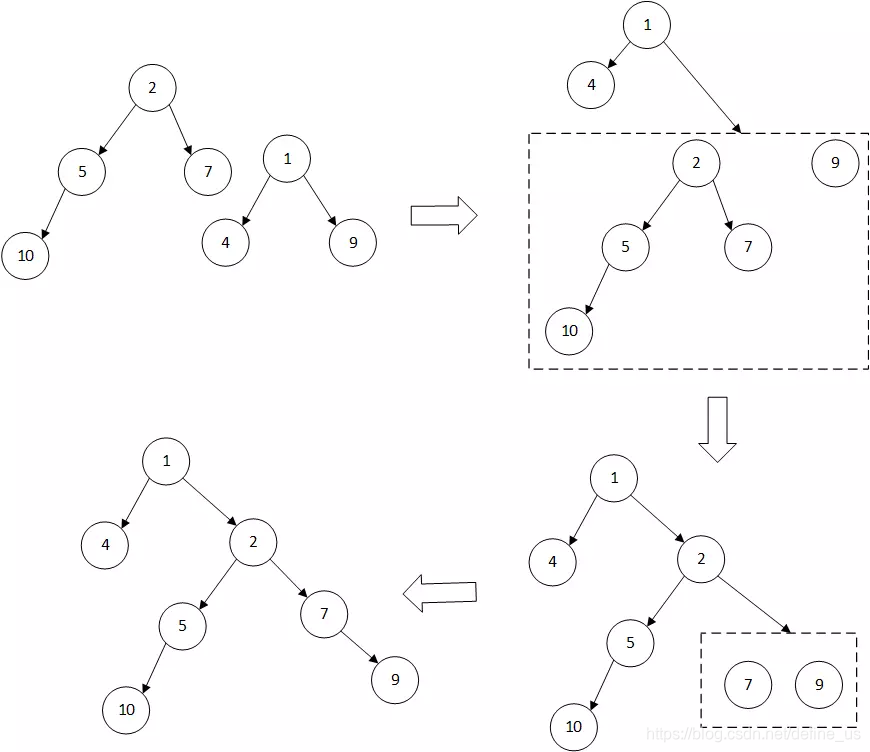
第二步,对于不符合的左式堆要求的节点,请调换左右节点。
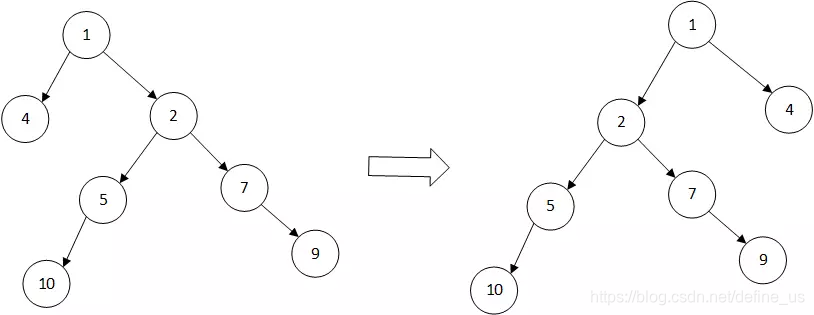
斜堆
斜堆是左式堆的自调节形式。其和左式堆的关系类似与伸展树和AVL树之间的关系。
二项队列
一个二项队列不是一棵树,而是树的集合,即森林。其中的每一棵树被叫做二项树(binomial tree)。高度为0的二项树是是一个单节点树。高度为k的树有2^k个节点。二项队列比如说以下形式
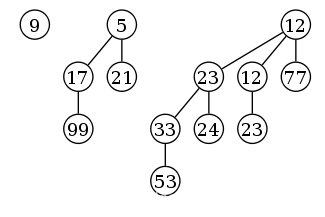
上面的二项队列包含三个二项树。那么,为什么叫二项树呢?上面第二棵树从上倒下层的节点数为121,第三棵树是1331。没错,如果这是一到找规律的脑残题目的话,你已经猜到了这就是二项系数。
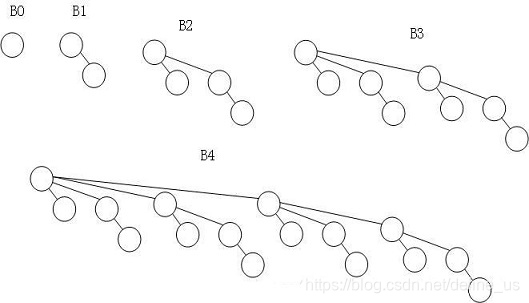
二项树的递归定义如下
二项树B0只有一个结点;
二项树Bk由两棵二项树B(k-1)组成的,其中一棵树是另一棵树根的左孩子。
二项树有以下的性质
Bk共有2k个节点。
Bk的高度为k。
Bk在深度i处恰好有二项系数C(k,i)个节点,其中i=0,1,2,...,k。
根的度数(子节点数)为k,它大于任何其它节点的度数。
在此基础上,我们可以定义二项队列
每棵二项树都满足最小堆性质。即,父节点的关键字 <= 它的孩子的关键字。
不能有两棵或以上的二项树具有相同的度数(包括度数为0)。换句话说,具有度数k的二项树有0个或1个。
下面是一个13个节点的二项队列。
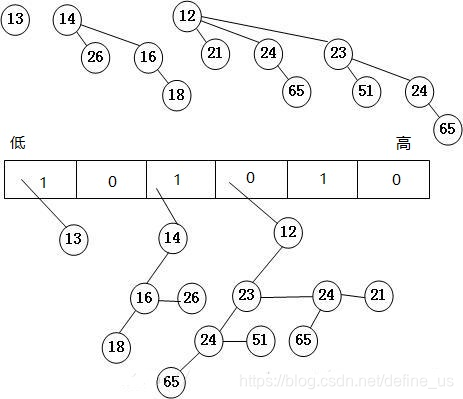
显然,二项队列查找最小值就是遍历所有二项树的根节点,然后找最小。





















 2318
2318










