朴素贝叶斯（Naive Bayes）

它是机器学习一个特别质朴而深刻的模型：当你要根据多个特征而非一个特征对数据进行分类的时候，我们可以假设这些特征相互独立（或者你先假设相互独立），然后利用条件概率乘法法则得到每一个分类的概率， 然后选择概率最大的那个作为机器的判定。

贝叶斯公式

如果AB都只有发生不发生两种状态，那么贝叶斯公式如下。其中P(B)表示B事件发生的概率。

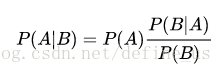
如果A,B两个事件独立（两个事件A和B是独立的当且仅当Pr(A∩B) = Pr(A)Pr(B)），P(B|A)=P(B)，也就没有计算的价值。但是，对于不是独立的AB两个事件，发生的概率存在一定关系，贝叶斯公式就是为了解决这个问题。

如果B事件有很多中状态，那么上面的式子变化为：

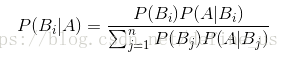
P(B|A)成为B的后验概率（发生A事件基础上的概率），而P(B)则是B事件的先验概率。

全概率公式

首先介绍完备事件群。说白了就是我们所说的一个事件有多种状态。下面B就是一个完备事件群。

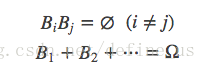
全概率公式如下：

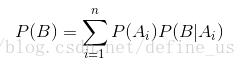
回头看贝叶斯公式，我们可以用自然语言将其叙述一遍，B完备事件群某状态的后验概率等于该状态的先验概率乘以事件A在该状态的后验概率，除以事件A的全概率。

朴素贝叶斯的实际应用