R-矩阵运算

最新推荐文章于 2024-06-29 14:45:19 发布

原创最新推荐文章于 2024-06-29 14:45:19 发布 · 362 阅读

0 ·

CC 4.0 BY-SA版权

数学与计算专栏收录该内容

434 篇文章

订阅专栏

本文详细介绍了矩阵的基本运算，包括矩阵的加减法、行列式的计算、转置运算、矩阵的乘法（内积与外积）及其几何意义。通过具体的例子展示了如何进行矩阵的运算，并解释了这些运算在实际应用中的意义。

> array(c(10,20,30,40),dim=c(2,2))->a
> a
     [,1] [,2]
[1,]   10   30
[2,]   20   40

行列式
> det(a)
[1] -200

转置运算
> t(a)
     [,1] [,2]
[1,]   10   20
[2,]   30   40

向量内积（点乘） a.b=x1*y1+x2*y2 其中a（x1,x2） b(y1,y2) 结果是标量一个数值

> x<-1:2
> y<-3:4
> x %*% y
[,1]
[1,] 11

上面是向量的，矩阵的结果是：

> a
     [,1] [,2]
[1,]   10   30
[2,]   20   40
> b
     [,1] [,2]
[1,] 100 300
[2,] 200 400
> a %*% b
      [,1] [,2]
[1,] 7000 15000
[2,] 10000 22000
>

上面是矩阵相乘，它只有在第一个矩阵的列数(column)和第二个矩阵的行数(row)相同时才有定义。一般单指矩阵乘积时，指的便是一般矩阵乘积。若A为m×n矩阵，B为n×p矩阵，则他们的乘积AB(有时记做A · B)会是一个m×p矩阵。其乘积矩阵的元素如下面式子得出：

$(AB)_{ij} = \sum_{r=1}^n a_{ir}b_{rj} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj}.$

由定义直接计算

左边的图表示出要如何计算AB的(1,2)和(3,3)元素，当A是个4×2矩阵和B是个2×3矩阵时。分别来自两个矩阵的元素都依箭头方向而两两配对，把每一对中的两个元素相乘，再把这些乘积加总起来，最后得到的值即为箭头相交位置的值。

$(AB)_{1,2} = \sum_{r=1}^2 a_{1,r}b_{r,2} = a_{1,1}b_{1,2}+a_{1,2}b_{2,2}$

$(AB)_{3,3} = \sum_{r=1}^2 a_{3,r}b_{r,3} = a_{3,1}b_{1,3}+a_{3,2}b_{2,3}$

下面这个是矩阵每个元素的乘法

> a*b
[,1] [,2]
[1,] 1000 9000
[2,] 4000 16000
>

向量外积（叉乘） a×b=|a|*|b|*sin<a,b> 结果是一个向量（矢量）

向量的外积是矩阵的克罗内克积的特殊情况。

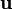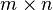给定 $m\times 1$ 列向量 $\mathbf{u}$ 和 $1 \times n$ 行向量 $\mathbf{v}$ ，它们的外积 $\mathbf{u} \otimes \mathbf{v}$ 被定义为 $m\times n$ 矩阵 $\mathbf{A}$ ，结果出自

$\mathbf{u} \otimes \mathbf{v} = \mathbf{A} = \mathbf{u} \mathbf{v}$

这里的张量积就是向量的乘法。

使用坐标:

$\begin{bmatrix}b_1 \\ b_2 \\ b_3 \\ b_4\end{bmatrix} \otimes \begin{bmatrix}a_1 & a_2 & a_3\end{bmatrix} = \begin{bmatrix}a_1b_1 & a_2b_1 & a_3b_1 \\ a_1b_2 & a_2b_2 & a_3b_2 \\ a_1b_3 & a_2b_3 & a_3b_3 \\ a_1b_4 & a_2b_4 & a_3b_4\end{bmatrix}$