数字图像与机器视觉基础实例

一、理论基础

①奇异值分解(SVD)原理与在降维中的应用

转自：奇异值分解(SVD)原理与在降维中的应用 - 刘建平Pinard - 博客园

奇异值分解

   奇异值分解(SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。

SVD的定义

  　SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×n的矩阵，那么我们定义矩阵A的SVD为：

A=UΣVT

其中U是一个m×m的矩阵，Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n×n的矩阵。U和V都是酉矩阵，即满足UTU=I,VTV=I。下图可以很形象的看出上面SVD的定义：

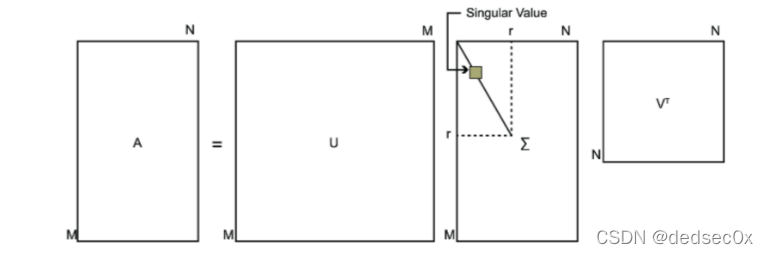
 　那么我们如何求出SVD分解后的U,Σ,V这三个矩阵呢？

　如果我们将A的转置和A做矩阵乘法，那么会得到n×n的一个方阵ATA。既然ATA是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

(ATA)vi=λivi

　这样我们就可以得到矩阵ATA的n个特征值和对应的n个特征向量v了。将ATA的所有特征向量张成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。如果我们将A和A的转置做矩阵乘法，那么会得到m×m的一个方阵AAT。既然AAT是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

(AAT)ui=λiui

这样我们就可以得到矩阵AAT的m个特征值和对应的m个特征向量u了。将AAT的所有特征向量张成一个m×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。U和V我们都求出来了，现在就剩下奇异值矩阵Σ没有求出了。由于Σ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ就可以了。

我们注意到:

A=UΣVT⇒AV=UΣVTV⇒AV=UΣ⇒Avi=σiui⇒σi=Avi/ui

这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵Σ。上面还有一个问题没有讲，就是我们说ATA的特征向量组成的就是我们SVD中的V矩阵，而AAT的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。

A=UΣVT⇒AT=VΣTUT⇒ATA=VΣTUTUΣVT=VΣ2VT

上式证明使用了:UTU=I,ΣTΣ=Σ2。

可以看出ATA的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到AAT的特征向量组成的就是我们SVD中的U矩阵。进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：

σi=λi−−√

这样也就是说，我们可以不用σi=Avi/ui来计算奇异值，也可以通过求出ATA的特征值取平方根来求奇异值。

②图像的开闭运算(腐蚀-膨胀)

摘自：图像的腐蚀(erode)和膨胀(dilate) 开运算以及闭运算 - MATLAB论坛 - 数学建模社区-数学中国

腐蚀和膨胀是数学形态学上的名词，如果用于图像处理上则就称为图像二值形态学。形态学主要是为了获取物体的拓扑和结构信息，通过物体和结构元素相互作用的某些运算，得到物体更本质的形态。当形态学运用到图像处理中，它的主要作用是利用形态学的基本运算，如腐蚀和膨胀运算，对图像进行观察和处理，从而达到改善图像质量的目地；描述和定义图像的各种几何参数和特征
腐蚀的具体操作：用一个结构元素(也可以说成操作数矩阵)一般为3×3大小的，也可以看成一个卷积模板，它们的区别就在于卷积模板是以算术运算为基础的，而结构元素是以集合运算为基础的，扫描图像中的每一个像素(关于图像边缘的处理见下面详细分析)，用操作数矩阵扫描图像中的每一个像素，操作数矩阵中每一个像素与覆盖的像素做“与”操作，如