【原理】如何形象地理解交叉熵-信息熵

最新推荐文章于 2025-08-10 14:13:11 发布

原创最新推荐文章于 2025-08-10 14:13:11 发布 · 1.3k 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习

机器学习专栏收录该内容

5 篇文章

订阅专栏

本文来自《老饼讲解-BP神经网络》https://www.bbbdata.com/

一、信息量

1.1.什么是信息量

信息量是对信息的一种量化指标，用于衡量信息的大小，最常用的是香农信息量，香农信息量的定义与计算公式如下：
$h(x)=−\ln(p(x))$

其中，p是事件x发生的概率，h则为事件x所包含的香农信息量。
从式中可以看到，事件的香农信息量与事件的概率成反比，
香农信息熵
即一件事发生的概率越小，则包含的信息量越大

二、什么是信息熵

2.1.什么是信息熵

信息熵通俗来说就是信息量的期望，香农信息熵则是香农信息量的期望
如果已知 x 有 n 种取值，且知道每种取值的概率，则 x 的香农信息熵如下：
$\displaystyle H(x) = -\sum\limits_{i}^{n}p(x_i)\ln p(x_i)$

2.2. 信息熵的意义

为什么要单独把"信息量的期望"单独拎出来命名为"信息熵"呢？因为信息熵是一个常用的概念，例如用信息熵来评估事件的混沌程度，当我们对一个事件越不确定时，即越混沌时，在得知该事件的确切值时期望获得的信息量就越多，即事件越混沌，事件的信息熵就越大：
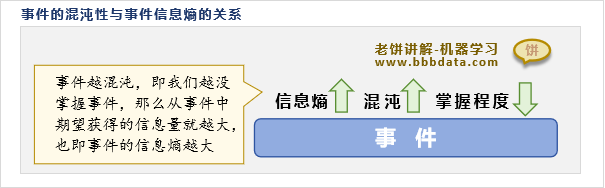
信息熵用于评估事件的混沌性
因此，一般可用信息熵来评估一个事件的混沌程度，或者我们对事件的掌握程度

三、交叉熵

3.1.什么是交叉熵

如果已知 X 有 n 种取值，我们认为第 i 种取值的概率为 $q(x_i)$ ,事实上第i种取值的概率为 $p(x_i)$ ,则定义在知道X的真实取值时所获得的信息量期望为交叉熵
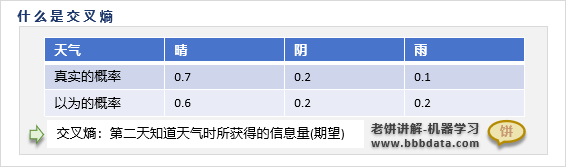
什么是交叉熵
香农交叉信息熵的公式如下：
$\small \displaystyle C(p,q) = -\sum\limits_{i}^{n}p(x_i)\ln q(x_i)$

3.2.如何理解交叉熵的意义

交叉熵经常用于评估概率模型的预测效果的准确程度，交叉熵越小，说明模型越准确
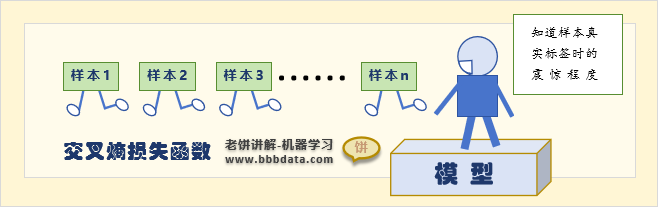
交叉熵的意义
为什么交叉熵越小，模型就越准确呢？
因为交叉熵就是知道X的真实取值时所获得的信息量期望，交叉熵越小，说明信息量越小。
模型的交叉熵越小(知道真实标签时的信息量小)，那说明基于模型我们已经基本掌握了样本的标签类别信息了。