关于数据拟合问题会用到的代码

代码一

用 Python 代码生成一个 5 Hz 的纯正弦信号，并计算 DFT 观察频谱

代码

import numpy as np
import matplotlib.pyplot as plt

# 采样率和时间设置
fs = 100  # 采样率 100 Hz
T = 1.0 / fs  # 采样间隔
N = 100  # 采样点数
t = np.arange(N) * T  # 时间向量

# 生成 5 Hz 的纯正弦波信号
f0 = 5  # 频率 5 Hz
A = 3   # 振幅 3
x = A * np.sin(2 * np.pi * f0 * t)

# 计算 FFT
X = np.fft.fft(x)
freqs = np.fft.fftfreq(N, T)

# 只取正频率部分
N_half = N // 2
freqs_half = freqs[:N_half]
X_mag_half = np.abs(X[:N_half]) / (N / 2)  # 归一化，使振幅正确

# 画出时域信号
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(t, x, 'r')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Time Domain Signal')

# 画出 FFT 频谱
plt.subplot(1, 2, 2)
plt.stem(freqs_half, X_mag_half)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.title('Frequency Domain (DFT via FFT)')

plt.tight_layout()
plt.show()

结果分析

运行代码后，你会发现：

1. 时域信号（左侧图像）是一个 5 Hz 的正弦波。
2. 频域信号（右侧频谱图）只有一个非零点，位于 5 Hz，振幅为 3（与原信号匹配）。
3. 其他频率的振幅接近零，符合理论预期。

FFT 计算的结果是对称的，负频率部分和正频率部分都会有一个峰值。这是因为 DFT 处理的信号是复数指数，其傅里叶变换具有共轭对称性。因此：

• 对于实信号，在 +f0+f0​ 和 −f0−f0​ 处都会有幅度峰值。
• 通常我们只取正频率部分来分析（即 N_half）

代码分析

1.

t = np.arange(N) * T  # 时间向量


#方法二：等价代码
t = np.linspace(0, (N-1)*T, N)

1.作用：计算每个采样点的时间值

2/采样频率、采样间隔、采样点数

1.）采样频率sr和采样间隔T: T = 1/sr

2.）采样频率：

        每秒采集多少次（定义了时间段是1s）[Hz]。采样频率由设备给出，不可人为更改。知道了采样频率sr，可以确定采样间隔T(隔多少秒采集一次)。

        rs与N: 知道了rs，就知道了一秒内的采样点数N（N = rs）。如果需要总的采样点数，乘多少秒即可。

3.）采样点数N

        人为规定，想采集多少个采集多少个点。一般流程：specific equipment 给了采样频率，规定采样时间（一共持续多少秒），就可以知道 N.

3.举例：

假设：

• 采样率 fs = 100 Hz（每秒采样 100 次）。
• 采样点数 N = 10。
• 采样间隔 T = 1 / fs = 1 / 100 = 0.01 秒。

执行：

import numpy as np

fs = 100  # 采样率 100 Hz
T = 1 / fs  # 采样间隔
N = 10  # 采样点数

t = np.arange(N) * T  # 计算时间向量
print(t)

输出：

[0.   0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09]

表示 N=10 个采样点，每个点的时间坐标分别是：

• 第 0 个点：0.00 秒
• 第 1 个点：0.01 秒
• 第 2 个点：0.02 秒
• ...
• 第 9 个点：0.09 秒

2.

X = np.fft.fft(x)
freqs = np.fft.fftfreq(N, T)

第一个代码--np.fft.fft(x) 

把时域信号通过fft方法（本质上时dft，但是fft比dft速度快），转换为频域信号。

计算信号 x 的 离散傅里叶变换（DFT），使用的是快速傅里叶变换（FFT） 算法，使计算更高效。

作用：

• 输入：时域信号 x（长度为 N）。
• 输出：频域信号 X（长度 N），结果是复数数组，包含振幅和相位信息。

第二个代码：freqs = np.fft.fftfreq(N, T)：计算频率坐标

DFT 计算的 X 结果包含 N 个数据点，每个点对应一个频率，np.fft.fftfreq(N, T) 用于计算这些频率值。

作用：

• 输入：
  • N：FFT 计算的点数
  • T：采样时间间隔（T = 1 / fs）
• 输出：一个数组，包含 N 个点的频率值，单位是 Hz。

np.fft.fftfreq(N, T) 生成的频率点分布如下：

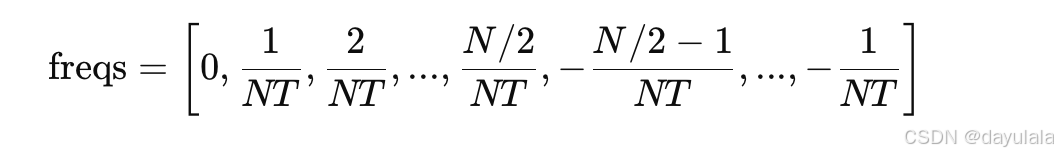
• 采样率：fs = 100 Hz
• 采样点数：N = 100
• 频率分辨率（df）：

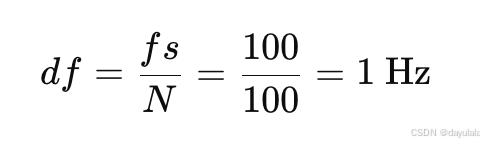
这意味着每两个频率点之间的间隔是 1 Hz。

 

最终 freqs 生成的频率范围是：

[0, 1, 2, 3, ..., 49, 50, -49, -48, ..., -1]

• 前半部分 [0,1,2,...,50][0,1,2,...,50] 是 正频率，表示信号的真实物理频率。
• 后半部分 [−49,−48,...,−1][−49,−48,...,−1] 是 负频率，表示数学上的共轭对称部分（对实信号来说是冗余的）。

时域信号-Time domain signal

        （1）时域信号：时间域下对应的信号

        （2）时域信号的长度 N ：有多少个数据点。 时域信号的长度= 采样点数

频域信号-Frequency domain signal

        （1）频域信号：频域下对应的信号，有幅值和频率两个信息。结果是复数数组，包含振幅和相位信息

        （2）频域信号的长度N

3.

# 只取正频率部分
N_half = N // 2
freqs_half = freqs[:N_half]
X_mag_half = np.abs(X[:N_half]) / (N / 2)  # 归一化，使振幅正确

3.1

N_half = N // 2

3.2

X_mag_half = np.abs(X[:N_half]) / (N / 2)  # 归一化，使振幅正确

4.绘图（time domain）和frequency domain注意、label标注

# 画出时域信号
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(t, x, 'r')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Time Domain Signal')

# 画出 FFT 频谱
plt.subplot(1, 2, 2)
plt.stem(freqs_half, X_mag_half)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.title('Frequency Domain (DFT via FFT)')

plt.tight_layout()
plt.show()

代码二

import numpy as np

# 生成简单的正弦波信号
fs = 100  # 采样率 100 Hz
T = 1 / fs  # 采样间隔
N = 100  # 采样点数
t = np.arange(N) * T  # 时间向量

# 5 Hz 正弦波
x = np.sin(2 * np.pi * 5 * t)

# 计算 FFT
X = np.fft.fft(x)

# 打印前 5 个 FFT 结果
print(X[:5])

[ 2.93915232e-15+0.00000000e+00j -3.38271078e-15-2.24907808e-15j
 -7.70371978e-15-7.22222854e-15j  6.64128317e-15-2.04142948e-14j
  2.74518957e-14-5.00000000e+01j]

Xk​ 代表信号在第 k 个频率分量上的贡献，即在不同频率下的投影。

由于 N=100，计算出的 X 也有 100 个点，每个点对应一个频率。

• FFT 计算了 所有可能的频率分量（从 0 Hz 到 Nyquist 频率 2fs​/2）。
• 即使你的信号只有 5 Hz，FFT 仍然会计算 其他所有频率，只是它们的振幅大部分接近零。

找出最大的频率分量

        即使你的信号只有 5 Hz，FFT 仍然会计算 其他所有频率，只是它们的振幅大部分接近零。

        FFT 计算的 X 包含 100 个频率点，其中只有 5 Hz 处是主要的非零值。

# 找出幅度最大的频率分量
X_magnitude = np.abs(X)  # 计算幅度
peak_freq = freqs[np.argmax(X_magnitude)]  # 取出最大值对应的频率

print(f"FFT 最高频率分量：{peak_freq} Hz")

计算幅值：np.abs()

计算相位角：np.angle()

import numpy as np

z = 3 + 4j  # 复数
phase = np.angle(z)  # 计算相位
print(phase)  # 输出相位（单位：弧度）

FFT结果需要归一化

比如：在时域中定义信号：x = np.sin(2 * np.pi * 5 * t) 【注意给了一个信号，关注信号两方面：振幅、频率】

代码三：

sampling rate :sr = 100

采样点数： N =100

时域信号：np.sin(2 * np.pi * 5 * t)

输出前6个经过fft转换后的频域信号及每个信号对应的频率、幅值、相位角

import numpy as np

# 生成简单的正弦波信号
fs = 100  # 采样率 100 Hz
T = 1 / fs  # 采样间隔
N = 100  # 采样点数
t = np.arange(N) * T  # 时间向量

# 5 Hz 正弦波 ，幅值1
x = np.sin(2 * np.pi * 5 * t)

# 计算 FFT
X = np.fft.fft(x)
freqs = np.fft.fftfreq(N, T)


#计算前6个fft结果的幅值
A = np.abs(X[:6])

#计算前6个fft结果的相位角
B = np.angle(X[:6])


# 打印前 6个 FFT 频率、幅值和相位角
for i in range(6):
    print(f"Frequency: {freqs[i]:.1f} Hz, Magnitude: {A[i]:.4f}, Phase: {B[i]:.4f}")

输出：

 

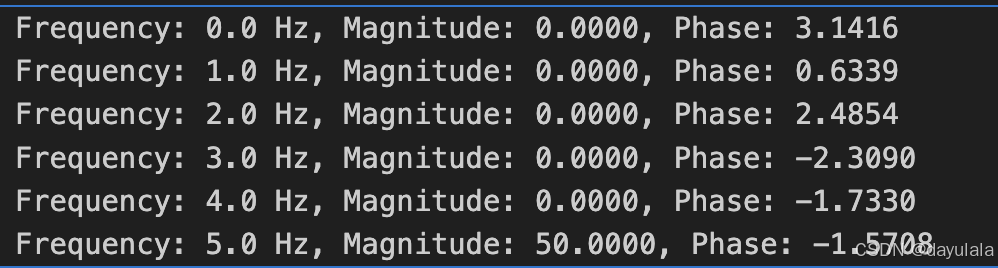
• 这个信号的振幅是 1。
• 但是，FFT 计算的结果中，5 Hz 处的幅值是 50，而不是 1。

这是因为 FFT 计算出的结果需要归一化（Normalization），否则幅值会与原信号不同。

FFT 计算时的数学原理

1. FFT 计算出的结果比原信号的振幅大 N/2 倍，因为 DFT 的计算公式是 求和，而不是求平均值。
2. 为了使 FFT 结果匹配时域信号的幅值，我们需要手动进行归一化：
   • 除以 N/2 以获得正确的幅度。
   • 由于 FFT 结果是对称的（对于实数信号），所以 只取前半部分时要乘以 2，最终归一化因子是 2/N。

重要概念

• FFT 计算出的 X[k] 累加了所有时域点的贡献，导致它的幅值被放大了 N/2 倍（对于实信号）。
• 因此，FFT 结果需要 除以 N/2 进行归一化，才能得到正确的振幅。

【理解】此例中共有100个采样点，每个采样点对应的频率都一样（因为单一频率的时域信号，所以都是5Hz）,所以如果不normolisation的话，经过反复天转化：频域内 频率=5 hz, 对应的X[k]实则为50*1= 50.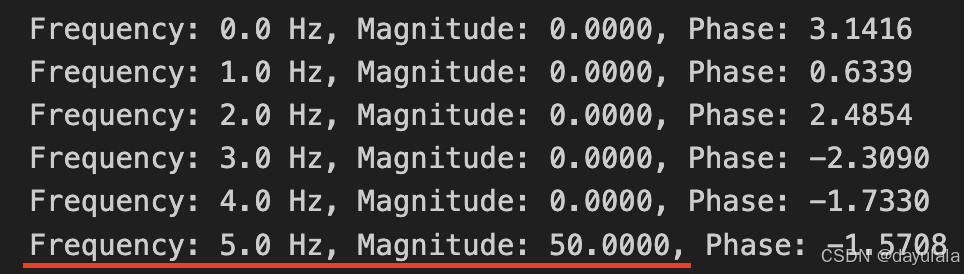

        另50个数据点对应：频率 = -5Hz 

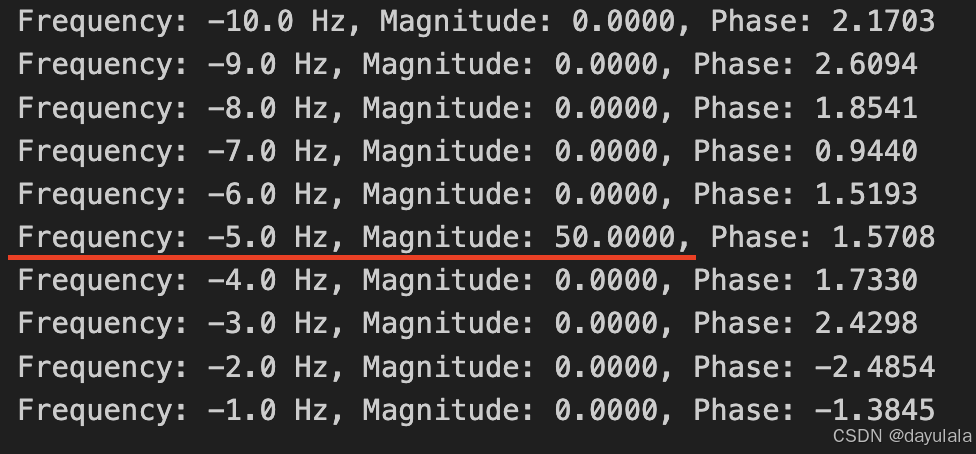
如何正确归一化 FFT 结果

 修改代码：

在 A = np.abs(X[:6]) 之后，添加 归一化操作：

A = np.abs(X[:6]) / (N / 2)  # 归一化

完整代码：

import numpy as np

# 生成简单的正弦波信号
fs = 100  # 采样率 100 Hz
T = 1 / fs  # 采样间隔
N = 100  # 采样点数
t = np.arange(N) * T  # 时间向量

# 5 Hz 正弦波
x = np.sin(2 * np.pi * 5 * t)

# 计算 FFT
X = np.fft.fft(x)
freqs = np.fft.fftfreq(N, T)

# 计算前 6 个 FFT 结果的幅值，并正确归一化
A = np.abs(X[:6]) / (N / 2)

# 计算前 6 个 FFT 结果的相位角
B = np.angle(X[:6])

# 打印前 6 个 FFT 结果
for i in range(6):
    print(f"Frequency: {freqs[i]:.1f} Hz, Magnitude: {A[i]:.4f}, Phase: {B[i]:.4f}")

DFT代替FFT

两种办法定义dtf：for双重循环、矩阵运算

代码操作：需改动两处

用discrete fourier transform rather than fast fourier transform:

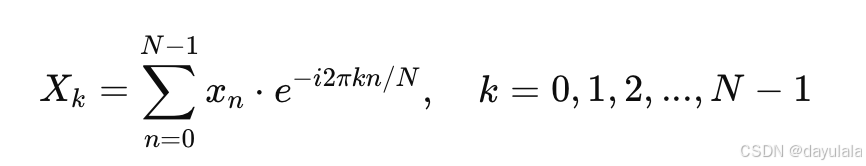
• np.fft.fft(x) → 需要手动定义 dft(x)。def dft（x）

方法一：for双重循环

def dft(x):
    """ 计算离散傅里叶变换 (DFT)"""
    N = len(x)
    X = np.zeros(N, dtype=complex)  # 结果存储复数
    for k in range(N):
        for n in range(N):
            X[k] += x[n] * np.exp(-2j * np.pi * k * n / N)
    return X

方法二：矩阵运算

def DFT(x):
    """
    Function to calculate the 
    discrete Fourier Transform 
    of a 1D real-valued signal x
    """

    N = len(x)
    n = np.arange(N)  # n = [0, 1, ..., N-1]
    k = n.reshape((N, 1))  # 生成列向量，形状 (N,1)
    e = np.exp(-2j * np.pi * k * n / N)  # 生成 N×N 的指数矩阵
    
    X = np.dot(e, x)  # 计算矩阵乘法（加速计算）
    
    return X

• np.fft.fftfreq(N, T) → 需要手动计算频率

特点：

• 双层 for 循环计算 DFT，时间复杂度为 O(N²)，比 FFT O(N log N) 慢得多。
• 计算频率坐标：np.fft.fftfreq(N, T) 不能用，需手动计算

freqs = np.array([k / (N * T) for k in range(N)])

• 归一化normalisation修正：

DFT 计算的结果仍然是 N/2 倍，所以要手动归一化：

A = np.abs(X[:6]) / (N / 2)

 举例：代码五（同样为代码三中的问题）

# %%
sr = 100 #sampling rate
T = 1/sr #sampling interval
N = 100 #sampling number


x =  np.sin(2 * np.pi * 5 *t)



# 自定义 DFT 计算函数
def dft(x):
    """计算离散傅里叶变换 (DFT)"""
    N = len(x)
    X = np.zeros(N, dtype=complex)  # 结果为复数数组
    for k in range(N):
        for n in range(N):
            X[k] += x[n] * np.exp(-2j * np.pi * k * n / N)
    return X


X = dft(x)


# 计算 DFT
X = dft(x)

# 计算频率坐标 #frequency coordinate
freqs = np.array([k / (N * T) for k in range(N)])

# 计算前 6 个 DFT 结果的幅值和相位角，并进行归一化
A = np.abs(X[:6]) / (N / 2)  # 归一化，使幅值正确
B = np.angle(X[:6])  # 相位角

# 打印前 6 个 DFT 结果
for i in range(6):
    print(f"Frequency: {freqs[i]:.1f} Hz, Magnitude: {A[i]:.4f}, Phase: {B[i]:.4f}")

代码五：

*Example:* Generate 3 sine waves with frequencies 1 Hz, 4 Hz, and 7 Hz, amplitudes 3, 1 and 0.5, and phase all zeros. Add this 3 sine waves together with a sampling rate 100 Hz.

#%%
#example 
import numpy as np
import matplotlib.pyplot as plt

sr = 100 #sampling rate
T = 1/ sr #sampling interval
N = sr * 1 #sampling number
t = np.arange(N) * T

f1 = 1
x = 3 * np.sin( 2* np.pi * f1 * t)
f2 = 4
x += 1* np.sin(2*np.pi*f2*t)
f3 = 7
x += 0.5 * np.sin(2*np.pi*f3*t)

plt.plot(t,x,'or')
plt.xlabel('Time(s)')
plt.ylabel('Amplitude')
plt.title('Time Domain Signal')
plt.show()


#DFT
def dft(x):
    N = len(x)
    X = np.zeros(N,dtype= complex )
    for k in range(N):
        for n in range(N):
            X[k] += x[n] * np.exp(-2j* np.pi *k *n /N)
    return X

X = dft(x)


freqs = np.array([k / (N * T) for k in range(N)])#Calculate frequency

#Normalisation
N_half = N//2
freqs_half = freqs[:N_half]
X_mag_hal = np.abs(X[:N_half])/(N/2)

plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.stem(freqs_half,X_mag_hal,'b',markerfmt='',basefmt='-b')
plt.xlabel('Freq (Hz)')
plt.ylabel('Magnitude (Hz)')
plt.xlabel('DFT Domain Signal')

plt.subplot(1,2,2)
plt.stem(freqs_half,X_mag_hal,'b',markerfmt='')
plt.xlabel('Freq (Hz)')
plt.xlim(0,10)
plt.ylabel('Magnitude (Hz)')
plt.xlabel('DFT Domain Signal')

可能会用到的代码块

1.Normalisation

N_half = N//2
freqs_half = freqs[:N_half]
X_mag_hal = np.abs(X[:N_half])/(N/2)

2.画图time domain 和frequency domain

# 画出时域信号
plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.plot(t, x, 'r')
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.title('Time Domain Signal')

# 画出 FFT 频谱
plt.subplot(1, 2, 2)
plt.stem(freqs_half, X_mag_half)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.title('Frequency Domain (DFT via FFT)')

plt.tight_layout()
plt.show()

代码句子荟萃

plt.stem(freqs_half,X_mag_hal,'b',markerfmt='',basefmt='-b')

作用：绘制频谱图（幅度 vs 频率），它的作用是 使用 stem 图（茎叶图）来显示频谱数据。

参数：

 

f_welch, psd_welch = welch(x, fs, nperseg=nperseg, noverlap=noverlap)

Welch 方法 估计 功率谱密度 (PSD, Power Spectral Density)。

语句：

from scipy.signal import welch

f_welch, psd_welch = welch(x, fs, nperseg=nperseg, noverlap=noverlap)

参数说明：

• x: 输入信号（时间序列数据）
• fs: 采样频率 (Hz)
• nperseg: 每个段的长度（默认 256）
• noverlap: 每个段之间的重叠样本数（默认 nperseg // 2）

返回值：

• f_welch: 频率数组 (单位 Hz)
• psd_welch: 估计的功率谱密度 (PSD)