《人工智能现代方法（第4版）》第5章对抗搜索和博弈学习笔记-优快云博客

🎯 本章核心问题：当对面坐着个也想赢的家伙时，怎么下棋？

想象一下：

第3章：你在解一道数学题（题不会坑你）；
第4章：你在雾天找路（环境会坑你）；
第5章：你在和同桌考试争第一名（对手会故意坑你！）；

本章就是教你：在“零和游戏”中（你赢=他输），怎么做出最安全的决策。

一、基础设定：下棋前的“算账思维”

🔢 零和博弈：你家就是我家（的反面）

你的得分 + 对手的得分 = 0

翻译：你赚的每一分，都是对手亏的一分；
例子：象棋、围棋、五子棋、剪刀石头布；
关键心态：防对手最优，不是求自己最好；

🌲 博弈树：把所有可能的“杠”都想到

第1步：你走 → 第2步：他走 → 第3步：你走 → ... → 最终分数
       （你有3种走法）（每种他都有5种应法）（你再应...）

和普通搜索树的区别：

普通树：所有分支都是“机会”，选最好的就行；
博弈树：偶数层是对手在选，他会选对你最差的！

二、极小化极大算法：防杠精专用算法

🤔 核心思想：用最坏的恶意揣测对手

假设你在和商场老板砍价：

你想：最低价买到（分数越高越好）；
老板想：最高价卖出（让你的分数越低越好）；

🧮 算法三步走（以砍价为例）

第1步：建“讨价还价树”。

你开价：100元
├─ 老板答应 → 你赚：满意度80分
├─ 老板还价：120元
│    ├─ 你接受 → 你赚：满意度60分
│    └─ 你拒绝 → 交易失败：满意度0分
└─ 老板还价：150元
     ├─ 你接受 → 你赚：满意度30分
     └─ 你拒绝 → 交易失败：满意度0分

第2步：从最后往前推（逆推归纳）。

def 计算节点得分(节点):
    if 是最终结果:  # 叶子节点
        return 实际分数
    
    if 该你出价:  # MAX层（你希望分数高）
        return max(所有子节点分数)  # 选对你最有利的
    else:  # MIN层（老板希望分数低）
        return min(所有子节点分数)  # 选对你最不利的！

计算过程（从下往上）：

最底层（叶子）：
   答应100元：80分
   接受120元：60分
   拒绝120元：0分
   接受150元：30分
   拒绝150元：0分

倒数第二层（老板决策层）：
   你开100元后，老板有三个选择：
       答应：80分
       还120元 → 你最佳选择是接受（60分）
       还150元 → 你最佳选择是接受（30分）
   老板会选哪个？他会选让你分数最低的！
       还150元（30分）< 还120元（60分）< 答应（80分）
   所以老板会选：还150元 → 你只能得30分

最顶层（你决策层）：
   你开价100元 → 最终得30分（经过老板恶意选择后）
   如果开价80元呢？需要另算一棵树...

第3步：选择“最坏情况中最好的”。

每种开局，都假设对手会选对你最差的后续；
在所有这些“最差结果”里，选一个“相对最好的”；
这就是极小化极大值：max( min(对手所有恶心你的走法) )；

三、Alpha-Beta剪枝：少算点，省脑子

😫 问题：象棋全算完要算到宇宙灭亡

象棋平均每步35种走法；
一盘棋50步 → 35^100 种可能（数不清）；
但很多分支不用算就知道结果！

✂️ 剪枝原理：当你已经知道“这科考砸了”

场景：你在算期末总评，保研需要85分以上。

已确定：
   高数：90分（稳了）
   英语：正在算...
       听力部分对答案 → 最多能得20分/30分
       → 英语最多70分
       → 两科平均最多80分 < 85分
       → 不用细算阅读和作文了！直接放弃这科策略

🎮 算法版（Alpha：当前最好保证，Beta：对手最坏容忍）

def alpha_beta(节点, alpha, beta):
    if 节点是叶子:
        return 分数
    
    if 该你走:  # MAX层
        for 每个子节点:
            alpha = max(alpha, alpha_beta(子节点, alpha, beta))
            if alpha >= beta:  # 关键！
                break  # 剪枝！对手不会让你走到这里的
        return alpha
    else:  # MIN层（对手）
        for 每个子节点:
            beta = min(beta, alpha_beta(子节点, alpha, beta))
            if beta <= alpha:  # 关键！
                break  # 剪枝！你也不会让对手这么好过
        return beta

中国学生版理解：

Alpha：你妈对你的最低期望（“至少考上211”）；
Beta：你爸对你的最高容忍（“别复读就行”）；
剪枝：当你发现某科已经挂了，够不上211了 → 不用细算其他科了；

四、蒙特卡洛树搜索（MCTS）：不会算？那就模拟！

🎲 核心思想：不知道哪个工作好？就都去试岗一天

你毕业时有4个offer，不知道选哪个：

传统算法：分析行业前景、公司财报、个人匹配度...（累死）；
MCTS算法：每个公司去实习1个月，看哪家最爽；

🌳 四步循环（以选offer为例）

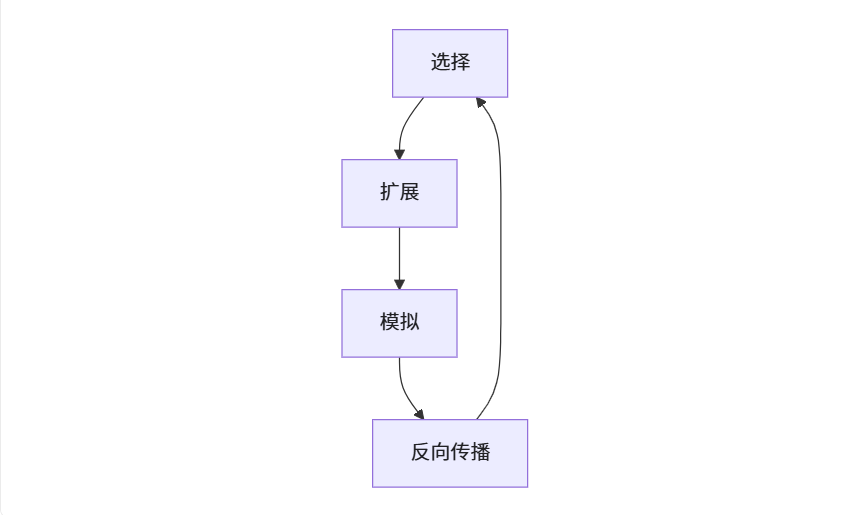
步骤1：选择（用UCB公式平衡探索与利用）

该去哪个公司试岗？
- 阿里：已经试过3次，平均满意度85分 →  exploitation（利用已知好的）
- 腾讯：只试过1次，得了90分 → 可能运气好？
- 字节：从来没试过 → exploration（探索未知）
UCB公式帮你量化这个纠结，选一个去试岗

步骤2：扩展

去选中的公司试岗，记录下感受；

步骤3：模拟

基于这次试岗，脑补如果长期在这工作会怎样（快速推演到年底）；

步骤4：反向传播

把模拟结果告诉之前的决策链： “选了互联网行业 → 选了阿里 → 选了这个部门 → 结果满意度70分” 更新这条路径上所有节点的“平均分”和“访问次数”；

♟️ 为什么AlphaGo强？

传统象棋AI：靠人类写的规则（“马走日”）；
AlphaGo：
- 初期：模仿人类棋谱（监督学习）；
- 后期：自己和自己下几百万盘（MCTS+强化学习）；
- 结果：走出人类从来没想过的“昏招”（后来发现是神招）；

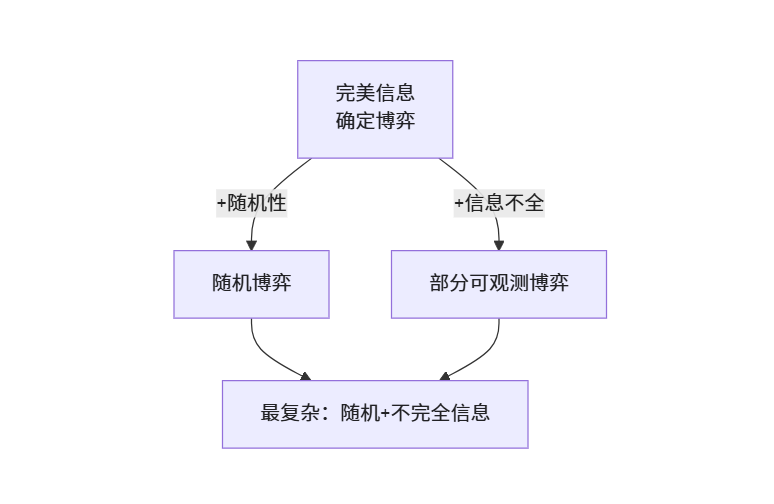
五、随机博弈：当游戏带“运气牌”

🎴 例子：打麻将

你的决策（打哪张牌）；
对手的决策（碰/杠/胡）；
随机因素：摸到的下一张牌是未知的！

⚖️ 期望值代替确定值

你要不要赌“听牌”？
- 听一张绝张（只剩1张在牌堆）：
    胡牌概率：1/30 ≈ 3.3%
    胡了得分：100分
    期望值：100 × 3.3% = 3.3分
    
- 听两头（还有8张可胡）：
    胡牌概率：8/30 ≈ 26.7%
    胡了得分：30分（番型小）
    期望值：30 × 26.7% = 8分

决策：选期望值高的（听两头），虽然胡了分数少，但容易胡到！

🌲 机会节点加入博弈树

你的决策层（MAX） → 对手决策层（MIN） → 发牌随机层（CHANCE） → ...
每个随机节点：计算所有可能的期望值

六、部分可观测博弈：打牌看不到对方手牌

🃏 典型场景：斗地主

你知道自己手里的牌（部分信息）；
你不知道两个对手各有什么牌；
你看到打出的牌（公共信息）；
你要推理：“他出这个2，是不是没王炸了？”

🤯 信念状态又来了！

初始：对手可能有任何17张牌的组合（天文数字）
他出第一张“3”：
→ 他一定有这张3
→ 他可能没有比3小的牌（如果有会更早出）
→ 更新“可能手牌集合”

本质：在对手可能手牌的分布上做极小化极大搜索。

💡 混合策略：有时候需要“诈唬”

石头剪刀布如果只出石头 → 对手发现后永远出布 → 你永远输；
正确策略：随机出（各1/3概率） → 对手无法预测；

算法实现：求解纳什均衡（找到一组概率，使得任何一方单方面改变都不会受益）。

七、实战算法选择指南

你的处境	适用算法	生活比喻
和同学下五子棋	极小化极大 + Alpha-Beta	算他接下来3步所有应法
参加围棋比赛	MCTS + 深度学习	用AI训练过的直觉+关键处深度计算
打麻将	期望极小化极大 + 信念更新	算概率+猜别人手牌
玩狼人杀	部分可观测博弈推理	从发言推断身份，可能故意说谎
商业谈判	博弈论纳什均衡	找到让双方都不想单方面毁约的方案