这是一本关于人工智能的百科全书,堪称人工智能教材的典范。本科时我曾在人工智能课上学过这本书的第3版。很多年过去了,深度学习给世界带来了惊喜,推动了自然语言处理、计算机视觉、机器人学的 快速发展,也为社会带来了伦理、公平性和安全性的新挑战。我很欣喜 地看到第4版引入了这些领域大量最新研究成果。如果你想了解人工智能的全貌,不要错过这本书。
——阿斯顿·张(Aston Zhang) 亚马逊资深科学家
一、本章核心思想
1.1 基本概念
- 问题求解智能体:通过“思考在前,行动在后”的方式,先规划再执行的智能体;
- 搜索:在脑海中模拟各种可能动作序列,寻找达到目标路径的计算过程;
- 关键假设:环境是完全可观测的、确定的、静态的、已知的;
1.2 问题求解的四个阶段
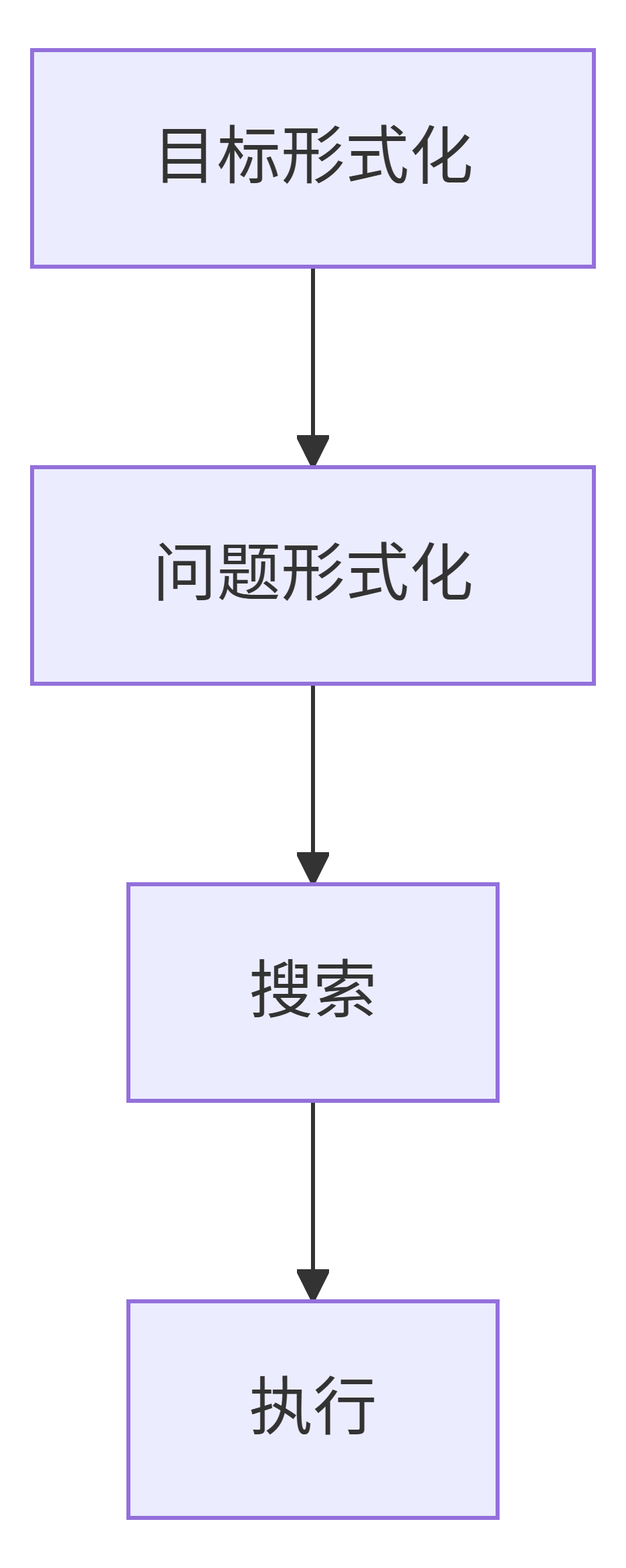
二、问题形式化(关键基础)
2.1 问题的五个组成部分
一个良定义的问题必须明确以下五个要素:
| 组件 | 符号表示 | 含义 | 示例(罗马尼亚旅行问题) |
|---|---|---|---|
| 初始状态 | s₀ | 智能体开始时的状态 | Arad |
| 动作集合 | Actions(s) | 在状态s下可执行的动作 | {GoSibiu, GoTimisoara, GoZerind} |
| 转移模型 | Result(s, a) | 执行动作a后的结果状态 | Result(Arad, GoSibiu) = Sibiu |
| 目标测试 | GoalTest(s) | 检查状态s是否为目标 | IsItBucharest(s) |
| 路径代价 | c(s, a, s′) | 动作消耗的代价 | 距离、时间、金钱等 |
2.2 抽象的重要性
- 抽象过程:忽略与现实目标无关的细节,构建简化模型;
- 示例:在罗马尼亚旅行问题中,只关注城市位置和道路,忽略油价、天气等;
- 有效性条件:抽象解必须能够被细化成真实世界的可行解;
三、搜索算法基础框架
3.1 搜索树概念
状态空间(图) → 搜索树(树状展开) → 解路径(动作序列)
3.2 基本数据结构:节点
每个节点包含:
- STATE:对应的状态;
- PARENT:生成该节点的父节点;
- ACTION:父节点生成该节点时采取的动作;
- PATH-COST:从初始状态到本节点的路径总代价,记为g(n);
3.3 搜索过程术语
| 术语 | 含义 |
|---|---|
| 扩展节点 | 用所有适用动作生成该节点的所有后继节点 |
| 边界(开放表) | 已生成但尚未扩展的节点集合 |
| 已达状态(封闭表) | 已经生成过节点的状态集合 |
3.4 冗余路径问题
- 循环:Arad → Sibiu → Arad → ...;
- 冗余路径:Arad直接到Sibiu(140km) vs Arad绕路到Sibiu(297km);
- 解决方法:记录已达状态,只保留到达每个状态的最优路径;
四、无信息搜索策略
4.1 算法评价标准
| 标准 | 含义 |
|---|---|
| 完备性 | 有解时一定能找到解吗? |
| 代价最优性 | 找到的解是最优(代价最小)的吗? |
| 时间复杂性 | 需要多长时间? |
| 空间复杂性 | 需要多少内存? |
4.2 五种无信息搜索算法对比
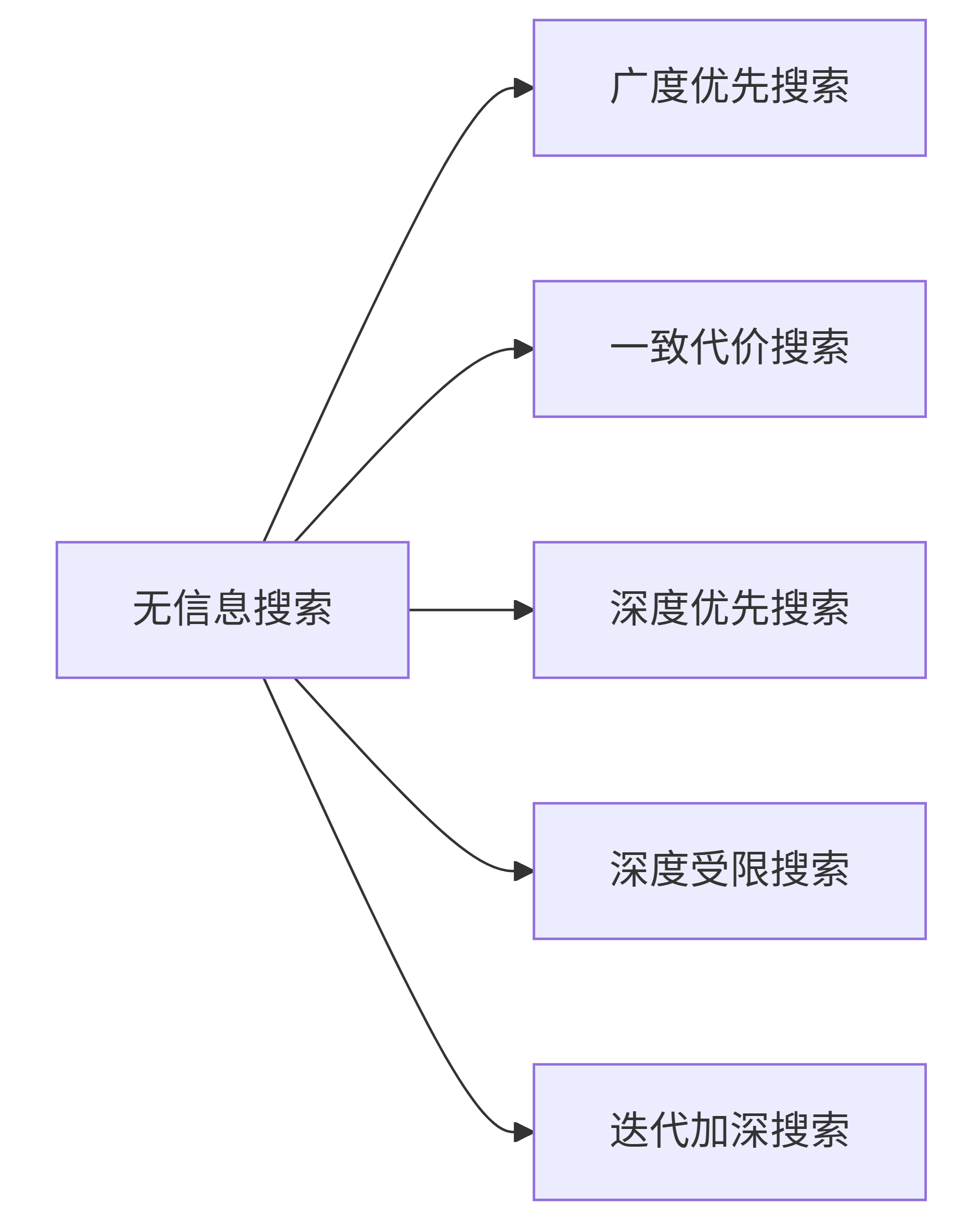
详细对比表
| 算法 | 评价函数f(n) | 完备性 | 最优性 | 时间复杂性 | 空间复杂性 | 特点 |
|---|---|---|---|---|---|---|
| 广度优先搜索 | 节点深度d(n) | 是 | 是(动作代价相同时) | O(b^d) | O(b^d) | 层层展开,内存消耗大 |
| 一致代价搜索 | 路径代价g(n) | 是 | 是 | O(b^(C*/ε)) | O(b^(C*/ε)) | 按代价递增顺序扩展 |
| 深度优先搜索 | -深度 | 否(无限空间) | 否 | O(b^m) | O(bm) | 内存需求小,可能陷入无限深度 |
| 深度受限搜索 | -深度(有界限l) | 否(解深度>l时) | 否 | O(b^l) | O(bl) | 避免无限深度,但不完备 |
| 迭代加深搜索 | -深度(界限递增) | 是 | 是(代价相同时) | O(b^d) | O(bd) | 结合BFS完备性与DFS内存效率 |
符号说明:
- b:分支因子(每个节点的平均后继数);
- d:最优解的深度;
- m:状态空间的最大深度;
- C*:最优解的代价;
- ε:最小动作代价;
五、有信息(启发式)搜索策略
5.1 启发式函数h(n)
- 定义:从节点n到目标的最优路径代价的估计值;
- 示例:直线距离hSLD(n);
- 要求:可采纳的启发式函数不能高估真实代价;
5.2 三种有信息搜索算法
5.2.1 贪心最佳优先搜索
- 评价函数:f(n) = h(n);
- 策略:优先扩展"看起来"最接近目标的节点;
- 特点:速度快,但不保证最优性,可能陷入局部最优;
5.2.2 A*搜索(最重要算法)
- 评价函数:f(n) = g(n) + h(n);
- 核心定理:如果h(n)是可采纳的(不高估),则A*是代价最优的;
- 一致性条件:h(n) ≤ c(n, a, n′) + h(n′),保证高效性;
5.2.3 加权A*搜索
- 评价函数:f(n) = g(n) + w × h(n),其中w > 1;
- 效果:更偏向目标,搜索更快,但解可能次优;
- 应用:当需要快速获得满意解而非最优解时;
5.3 A*搜索的等值线理解
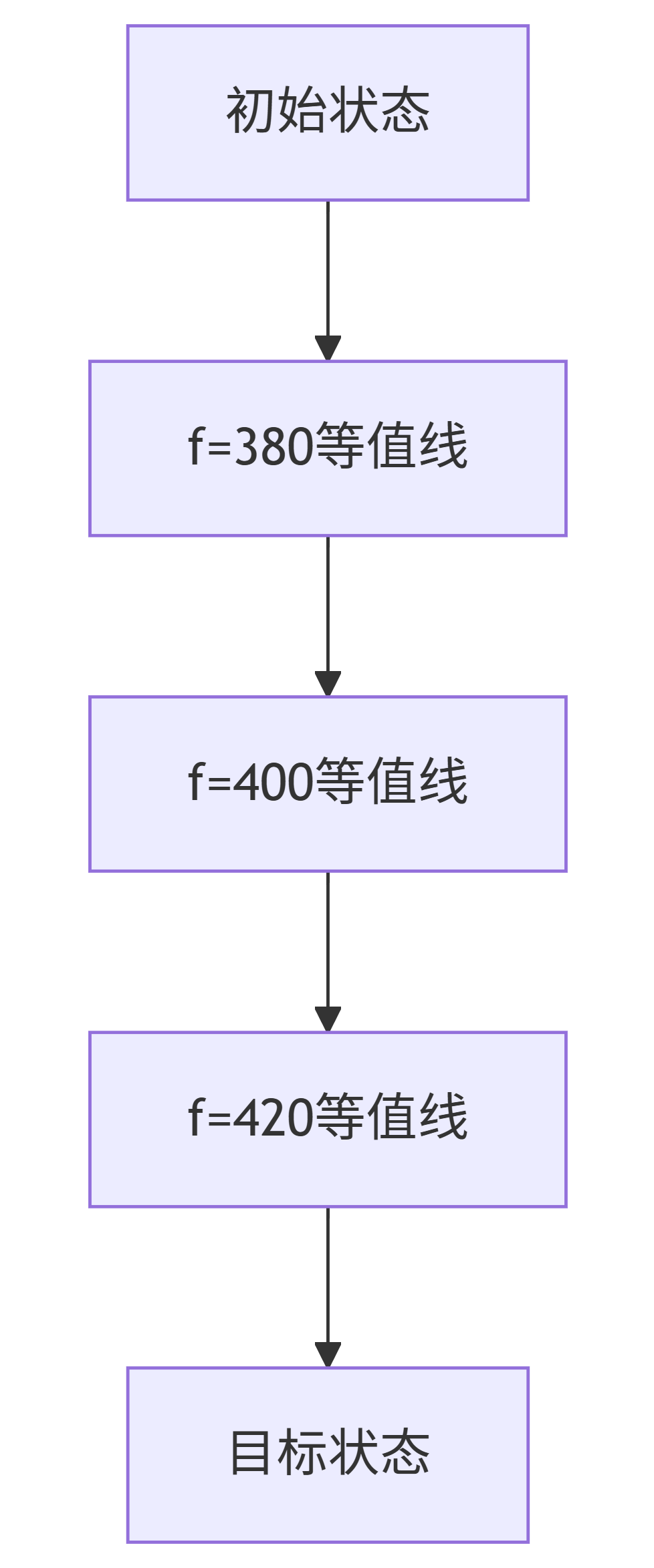
- A*从初始状态开始,按f值递增的顺序扇形扩展
- 必然扩展所有f(n) < C的节点(C是最优解代价)
六、启发式函数设计方法
6.1 启发式函数质量评价
- 有效分支因子b*:衡量搜索效率的指标;
- 占优关系:如果h₂(n) ≥ h₁(n)对所有n成立,则h₂优于h₁;
6.2 设计技术
| 方法 | 原理 | 示例 |
|---|---|---|
| 松弛法 | 通过简化问题生成可采纳启发式 | 8数码问题中忽略"滑块移动需空格"的条件 |
| 子问题法 | 求解子问题代价作为原问题下界 | 模式数据库存储子问题解代价 |
| 地标法 | 预计算到关键点的距离 | 导航系统中使用重要城市作为地标 |
| 机器学习 | 从经验数据中学习启发式函数 | 通过大量解样本训练估价函数 |
七、内存受限搜索
7.1 内存问题的重要性
- A*搜索需要存储整个边界和已达状态表;
- 大问题可能耗尽内存 → 需要内存受限算法;
7.2 主要算法
| 算法 | 核心思想 | 特点 |
|---|---|---|
| IDA* | 迭代加深A*,使用f代价作为截断值 | 线性空间,但可能重复扩展节点 |
| RBFS | 递归最佳优先搜索,线性空间复杂度 | 智能回溯,但计算复杂 |
| SMA* | 简化内存受限A*,丢弃最差节点 | 最优利用有限内存,是实际应用首选 |
八、关键概念总结
8.1 重要区别
- 状态空间 vs 搜索树:问题本身 vs 搜索过程生成的树;
- 图搜索 vs 树状搜索:检查重复状态 vs 不检查重复状态;
- 有信息 vs 无信息搜索:使用启发式函数 vs 不使用;
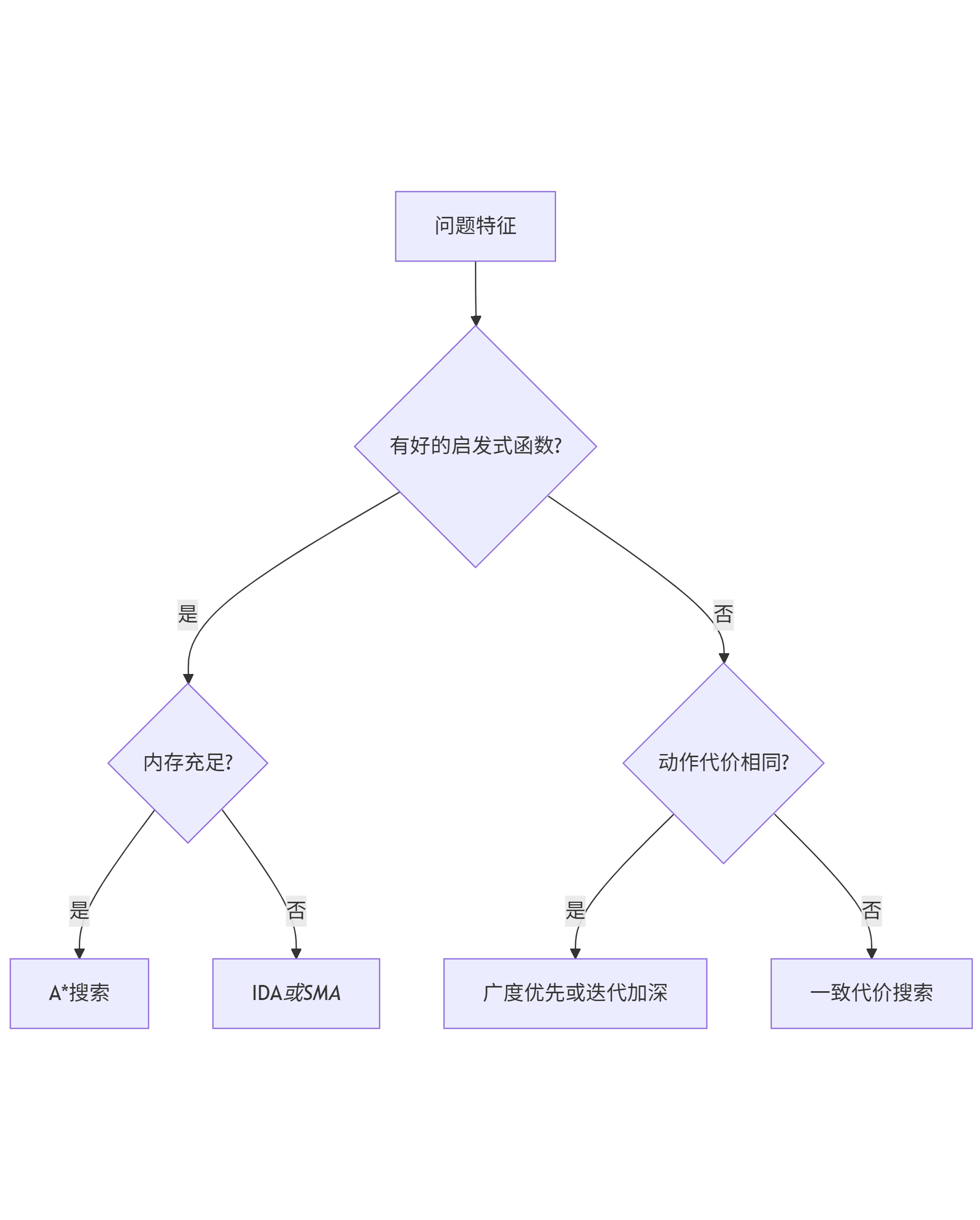
8.2 实用建议
- 小状态空间:广度优先搜索或迭代加深搜索;
- 动作代价不同:一致代价搜索;
- 有好的启发式函数:A*搜索;
- 内存受限:IDA或SMA;
- 需要快速满意解:加权A*搜索;
8.3 算法选择指南
🎯 第3章核心要点
- 搜索是问题求解的核心技术,适用于完全可观测的确定性环境;
- 问题形式化是成功的关键,必须明确定义五个组件;
- A*搜索是最重要的算法,结合了实际代价和启发式估计;
- 启发式函数质量决定搜索效率,好的启发式能指数级加速搜索;
- 内存管理在实际应用中至关重要,需要根据约束选择算法;
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








