再谈Dominator Tree的计算

我在《 构造Dominator Tree以及Dominator Frontier》介绍了支配树的相关概念以及它如何参与到SSA的构造过程中，但是在那一篇文章中我只介绍了cooper的基于数据流迭代的算法，但是在工程中还有一些其它的算法，例如llvm最早使用的 Lengauer-Tarjan algorithm 和2017年使用的 SEMI-NCA algorithm。

注：上图来源于《Finding Dominators in Flowgraphs Linear-Time Algorithm 1 and Experimental Study 2: Loukas Georgiadis》

Vertex-removal Algorithm

最直观的方法是节点删除法。例如在删除节点$w$之前，$v$不可达，但是删除$w$后，$v$不可达，我们就说$w$支配$v$。

注：上述算法来自于http://www.cs.au.dk/~gerth/advising/thesis/henrik-knakkegaard-christensen.pdf

The Iterative Algorithm Revisit

数据流迭代的算法的核心是下面的方程式$Dom(root)=root$。
$$Do{m}^{{}^{\prime }}(v)=(\bigcap _{v\in pred(v)}Do{m}^{{}^{\prime }}(u))\bigcup v,\forall v\in V-r$$

Finally, for any subset $U\subseteq V$ and a tree $T$, $NCA(T,U)$ denotes the nearest common ancestor of $U\bigcap T$ in $T$.

我们使用学到的数据流知识对这个方程式进行分析，首先它是一个MUST分析。

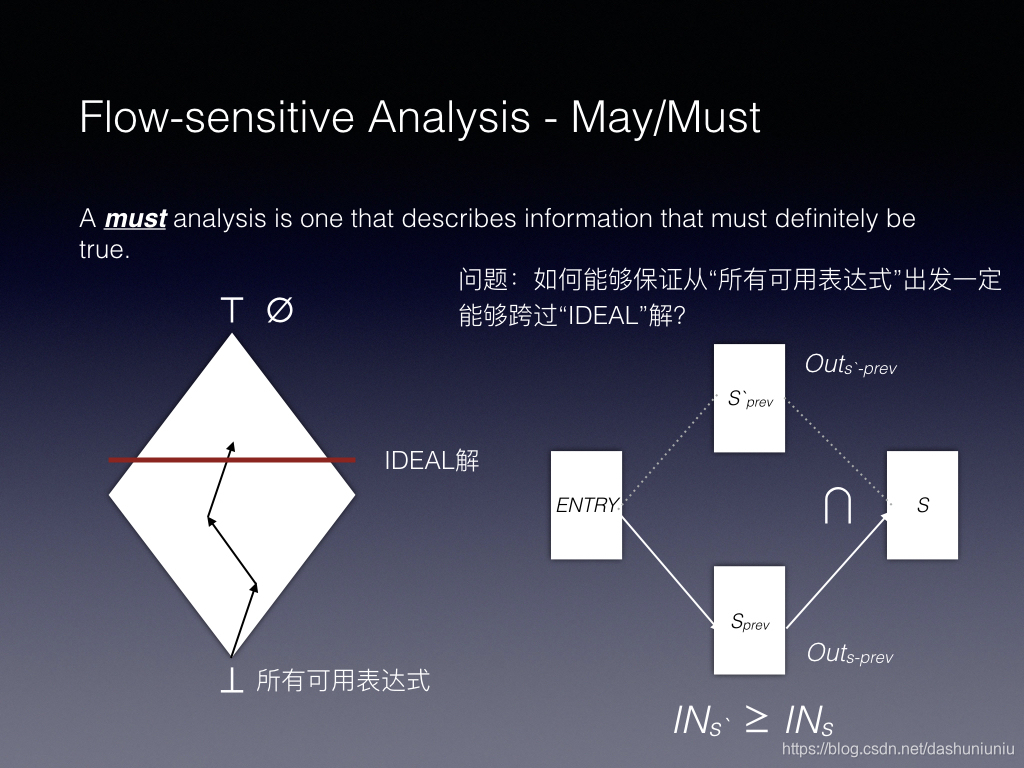
所以对应的算法如下。

注：上述算法来自于Cooper

Cooper对这种传统的基于迭代数据流计算$Dom$ set的方法进行了总结。

This algorithm produces correct results because the equations for Dom, as shown above, form a distributive data-flow framework as defined by Kam and Ullman [20]. Thus, we know that the iterative algorithm will discover the maximal fixed-point solution and halt. Since the framework is distributive, we know that the maximal fixed-point solution is identical to the meet-over-all paths solution—which matches the definition of Dom.

对于上面的描述，稍微岔开一下话题，介绍其中的几个关键点。因为有很多学习数据流分析的同学对这几个概念理解不是很透彻。

Distributive Data-Flow Framework

注：上图来源于#55 Distributive Framework for Data Flow Analysis

其实最开始的方程式分为两部分，

• 一部分是control flow equotion，也就是$i{n}_B={\bigcap }_{v\in pred(B)}Do{m}^{{}^{\prime }}(B)$
• 一部分是data flow equotion，也就是$ou{t}_B=i{n}_B\cup B$

我们能明显看到$tran{s}_B$是distribute的，如下图所示。

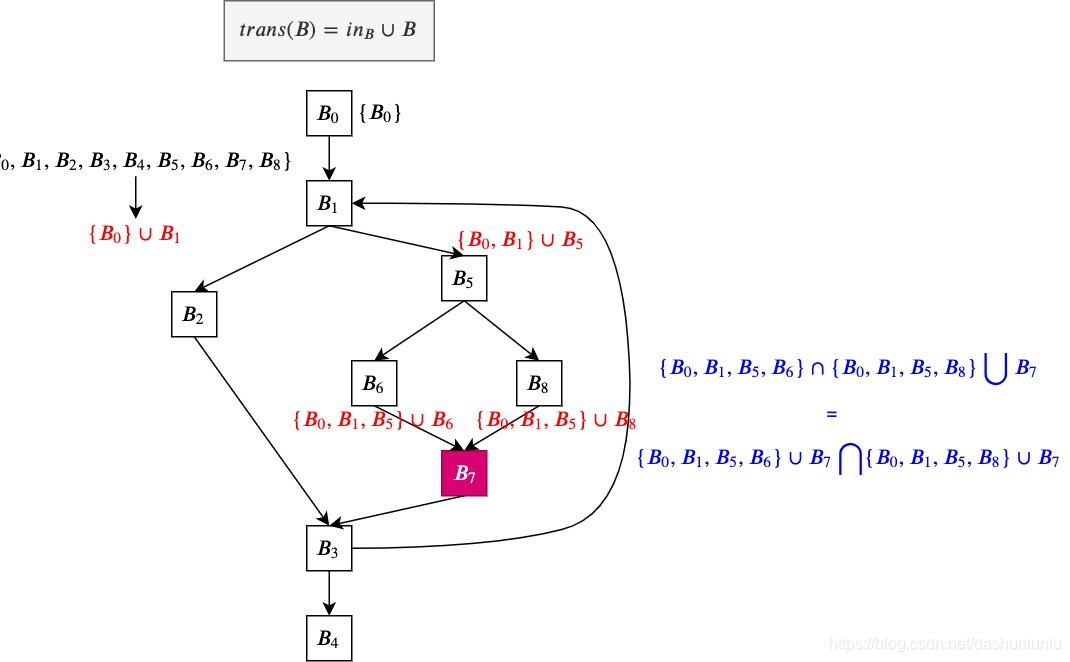
Distributive Framework最好的地方是能够保证 MFP解 = MOP解。

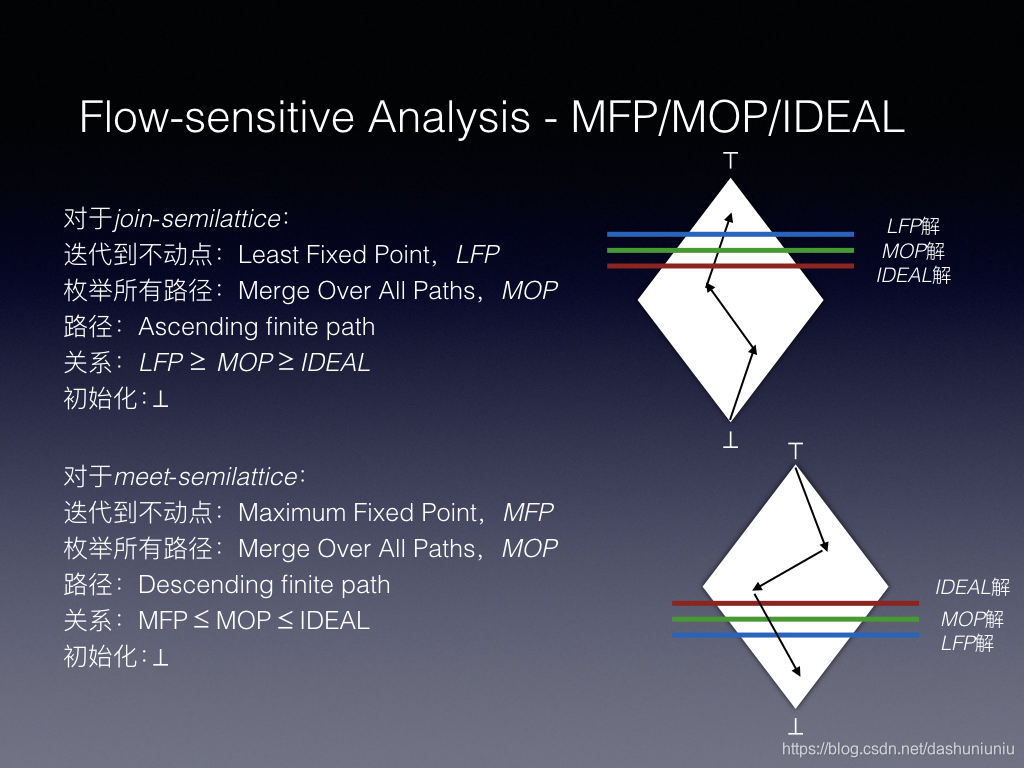
未来我再找机会解释$MOP$解为什么能够保证 $sound$。相关文章数据流分析中的Distributive Dataflow Problems

而Cooper对实现方式进行了改进，但是并没有改变数据流迭代的本质。可以参照构造Dominator Tree以及Dominator Frontier。主要是抽象出了dominator tree的概念，然后使用一个array存储了所有的dominator信息。

To improve the iterative algorithm’s performance, we need a memory-efficient data structure that supports a fast intesection.

Lengauer-Tarjan Algorithm Revisit

首先介绍一下Lengauer-Tarjan algorithm，我在《构造Dominator Tree以及Dominator Frontier》中提到过这个算法，但是当时我没有看懂，取而代之介绍了《Engineering a Compiler》中提到的迭代数据流的算法A Simple, Fast Dominance Algorithm。

LT算法基于下面已有的三个概念：

• preorder depth first search
• spanning tree
• immediate dominator

LT算法首先前序深度优先遍历Graph，然后给每个符号编号，如下图所示：

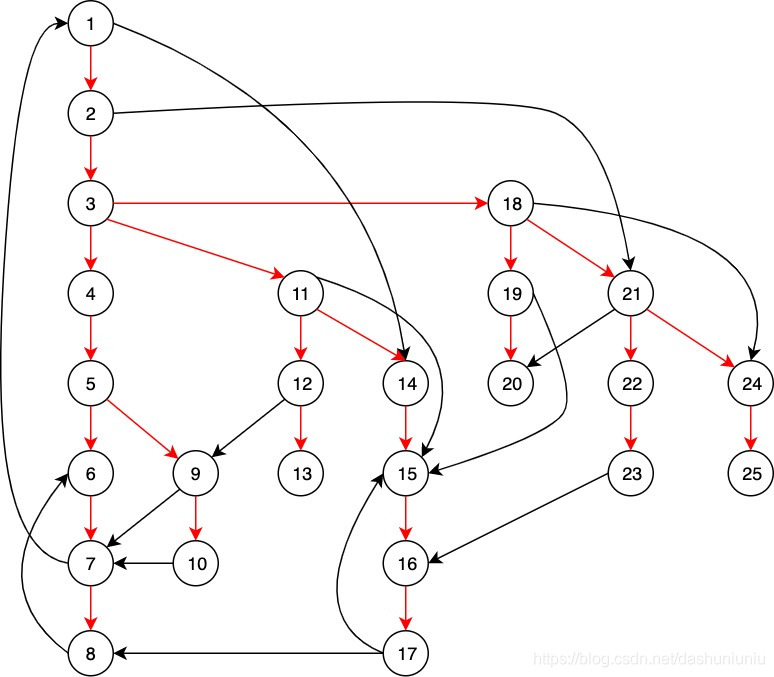
注：上图源于http://www.cse.unt.edu/~sweany/CSCE5934/HANDOUTS/LengaurTarjanOverheads.pdf

由于前序深度优先遍历得到的编号，LT算法创造了一个新的概念$semidominator$，简称为$sdom(w)$。$sdom$可以看做是对$idom$的一种逼近。

$sdom(w)$ = $min$ {$v$ | there is a path $v=v_0,v_1,...,v_k=w$ such that $v_i>w$ for $1\le i\le k-1$}

注：注意$i$的范围，$sdom(w)$一定是 $w$在spanning tree上的ancestor

A semidominator for a vertex $v$ in a Graph $G$ is an ancestor of $v$ in a DFS tree $T$ of $G$ and is used as an approximation of the immediate dominator of $v$. - 《Algorithms for Finding Dominators in Directed Graphs》

例如要计算sdom(15)，最小的值为2，下图中加粗的路径表示这条路径。其实除了这条路径之外，还有

• $14\to 15$
• $11\to 15$
• $3\to 18\to 19\to 15$
• … 其实 $19\to 15$也算，但是既然找$min$值，所以我只把值得考虑的列了上来。
  
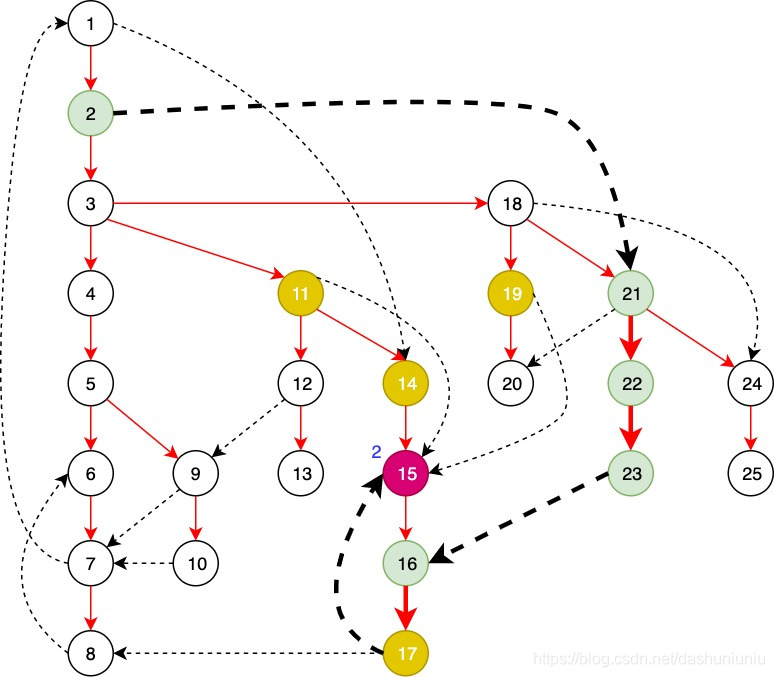
  注：我把非spanning tree的边描成了虚线

如果我们把所有节点的$sdom$值列出来的话，如下图所示。我们可以发现对于大部分节点来说，$sdom$和$idom$值都相同。而7、15、16、24的$sdom$和$idom$不相同，而导致不相同的路线我都用绿色加粗标识了出来。

• $7$ 的 $sdom$ 是3，$idom$ 是1。
• $15$ 的 $sdom$ 是2，$idom$ 是1。
• $16$ 的 $sdom$ 是2，$idom$ 是1。
• $24$ 的 $sdom$ 是18，$idom$ 是2

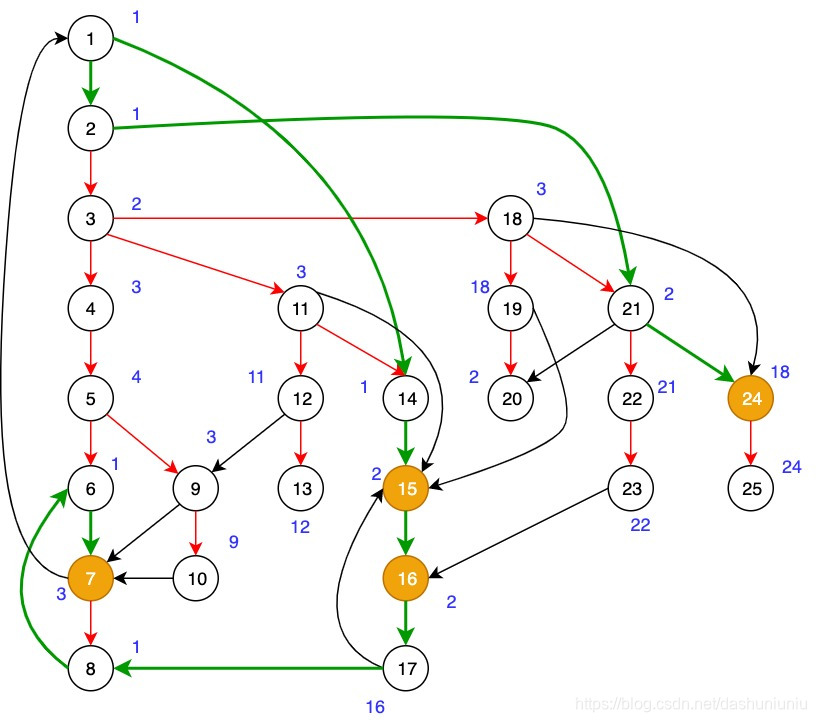
所以这里有以下两个问题：

• 如何 $sdom\to idom$
• 如何计算 $sdom$

为了解决上述的两个问题，我们先列出以下几个核心事实：

• If $w\ne r$ is any vertex, then $sdom(w)$ is a proper ancestor of $w$ in $T$.
• $idom(w)$ is a (not necessarily proper) ancestor of $sdom(w)$.
• If we replace the set of nontree edges of $G$ by the set of edges { ( s d o m ( w ) , w ) ∣ w ∈ V a n d   w ≠ r } \{(sdom(w), w) | w \in V and\ w \neq r\} {(sdom(w),w)∣w∈Vand w​=r}, then the dominators of vertices in $G$ are unchanged.
• Thus if we know the spanning tree and the semidominators, we can compute the dominators.

注：上面的$T$表示的是深度优先遍历得到的spanning tree，$G$表示原始的图

为了解决上述两个问题，给出四个个引理：

LEMMA 2. For any vertex $w\ne r$, $idom(w)\stackrel{+}{\to }w$
LEMMA 3. For any vertex $w\ne r$, $sdom(w)\stackrel{+}{\to }w$
LEMMA 4. For any vertex $w\ne r$, $idom(w)\stackrel{\ast }{\to }sdom(w)$
LEMMA 5. For any vertices $v$, $w$ satisfy $v\stackrel{\ast }{\to }w$. Then $v\stackrel{\ast }{\to }idom(w)$ or $idom(w)\stackrel{\ast }{\to }idom(v)$

通过Lemma 5，我们就可以通过 semidominators 计算 immediate dominators 。

THEOREM 2. Let $w\ne r$. Suppose every $u$ for which $sdom(w)\stackrel{+}{\to }u\stackrel{\ast }{\to }w$ satifies $sdom(u)\ge sdom(w)$. Then $idom(w)=sdom(w)$.

THEOREM 3. Let $w\ne r$ and let $u$ be a vertex for which $sdom(u)$ is minimum among vertices $u$ satisfying $sdom(w)\stackrel{+}{\to }u\stackrel{\ast }{\to }w$. Then $sdom(u)\le sdom(w)$ and $idom(u)=idom(w)$.

COROLLARY 1. Let $w\ne r$ and let $u$ be a vertex for which $sdom(u)$ is minimum among vertices $u$ satisfying $sdom(w)\stackrel{+}{\to }u\stackrel{\ast }{\to }w$. Then

$$idom(w)=\{\begin{array}{l}sdom(w)\text{if sdom(w) = sdom(u)}\\ idom(u)\text{otherwise}\end{array}$$

具体实现

DFS

第一步深度优先遍历得到一个DFS Tree，并给各个节点标preorder number。

计算semidominators

首先，深度优先遍历Graph给各个节点标 preorder 序号。然后以reverse preorder的方式处理每一个节点，因为根据$sdom(v)$的定义，我们需要考虑一些order大于 $v$ 的节点的信息，以reverse order的方式处理的话，每当我们处理一个节点时，所需要的信息已经准备好了。

1. 对于节点$v$来说，我们可以轻松找到所有 predecessor 中小于$v$的节点中最小的那一个。例如最开始图中的节点15，它有两个predecessor小于15，分别是11和14，我们可以很轻松的得到11是这些predecessor中最小的一个。
2. 收集predecessor序号大于$v$的的path。假设predecessor为$q$，$q$的semidominator path为$(v_0,v_1,...,v_k=q)$，$q>v$，我们需要通过这些$q$的$sdom(q)$值计算$sdom(v)$。如果$v_0>v$，那么递归地找$sdom(sdom(...(sdom(v_0)))$，直到找到一个$v_i<v$。
3. 最终求1和2中的最小值。

如果对于下图来说，假设我们需要计算$sdom(15)$，我们已经收集到

1. predecessor值小于$15$的有$11$，$14$
2. 对于predecessor $19$，$sdom(sdom(19))=3$
3. 对于predecessor $17$，$sdom(sdom(17))=2$
4. $min(11,14,3,2)=2$

注：predecessor对应于Graph，parent对应于Tree

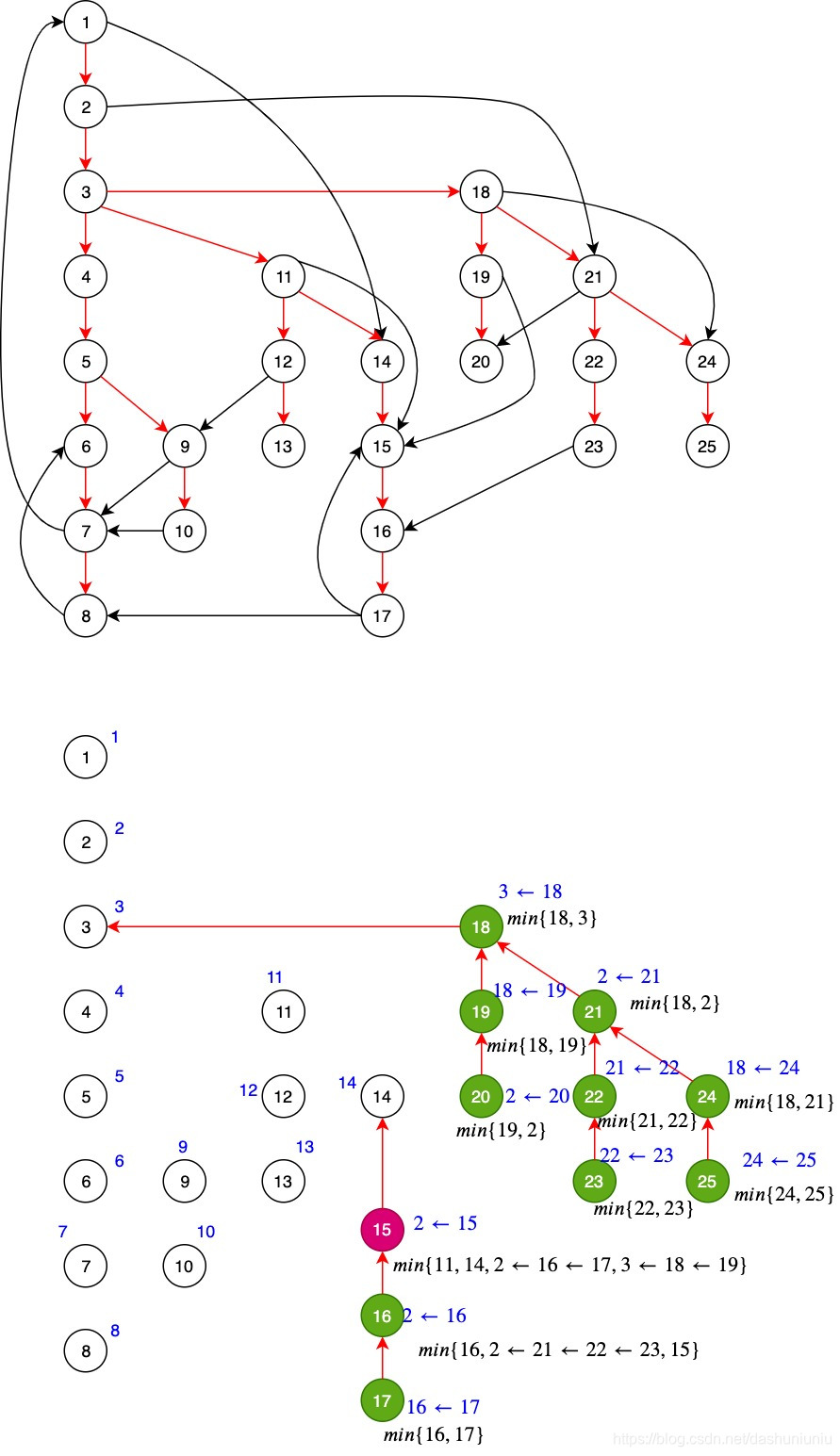
整体算法框架如下图所示：

注：上图来源于http://www.cs.au.dk/~gerth/advising/thesis/henrik-knakkegaard-christensen.pdf

eval & link

注：上图来源于《Finding Dominators in Flowgraphs Linear-Time Algorithm and Experimental Study》

在实现过程中，还是但很多可以优化的点。

计算$idom$

前面我们已经计算得到了各个节点的$sdom$，而且根据COROLLARY 1，我们已经知道什么情况下$sdom$等于$idom$，什么情况下$idom$需要通过$sdom$推导出来。

我们重新回顾一下前面介绍的几条定理，

THEOREM 2. Let $w\ne r$. Suppose every $u$ for which $sdom(w){\stackrel{+}{\to }}_{T}u{\stackrel{\ast }{\to }}_{T}w$ satifies $sdom(u)\ge sdom(w)$. Then $idom(w)=sdom(w)$.

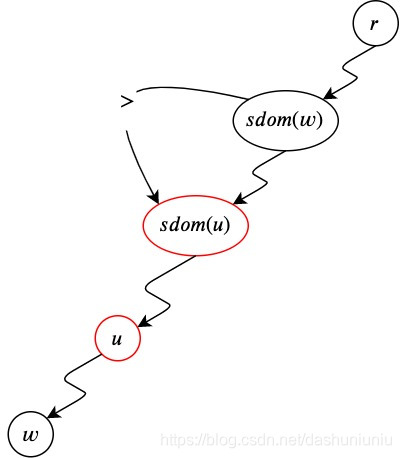
类似于下图中的节点$9$，$sdom(9)=3{\to }_{T}4{\to }_{T}5{\to }_{T}9$，其中$sdom(4)=3<sdom(9)$，$sdom(5)=4<sdom(9)$，所以 $idom(9)=sdom(9)$。

THEOREM 3. Let $w\ne r$ and let $u$ be a vertex for which $sdom(u)$ is minimum among vertices $u$ satisfying $sdom(w){\stackrel{+}{\to }}_{T}u{\stackrel{\ast }{\to }}_{T}w$. Then $sdom(u)\le sdom(w)$ and $idom(u)=idom(w)$.

对于定理3，可以参见上图中的节点$16$，$sdom(16)=2{\to }_{T}3{\to }_{T}11{\to }_{T}14{\to }_{T}15{\to }_{T}16$。 i d o m ( 16 ) = m i n { s d o m ( 3 ) = 2 ， s d o m ( 11 ) = 3 , s d o m ( 14 ) = 1 } = 1 idom(16) = min\{sdom(3)=2，sdom(11)=3, sdom(14)=1 \} = 1 idom(16)=min{sdom(3)=2，sdom(11)=3,sdom(14)=1}=1。注意这两个定理中的 path 不是 semidominator path，二是在 spanning tree中的path。

整个LT算法如下图所示：

注：上图中算法来自于http://www.cs.au.dk/~gerth/advising/thesis/henrik-knakkegaard-christensen.pdf

LT算法真的是复杂的一批。核心思想是求得$idom$的逼近值$sdom$，然后基于$sdom$，根据不同的情况推导出$idom$，算法细节见《Algorithms for Finding Dominators in Directed Graphs》。

The SEMI-NCA Algorithm

从算法的名字我们可以看出来，这个算法是 semidominator + nearest common ancestor(NCA) 组合起来的。

这个算法使用LT算法的前半部分，也就是计算$sdom$的部分。而后半部分使用下面的引理计算$idom$。它核心思想是，在 preorder 的方式遍历DFS spanning tree，以递增的方式创建dominator tree $D$。

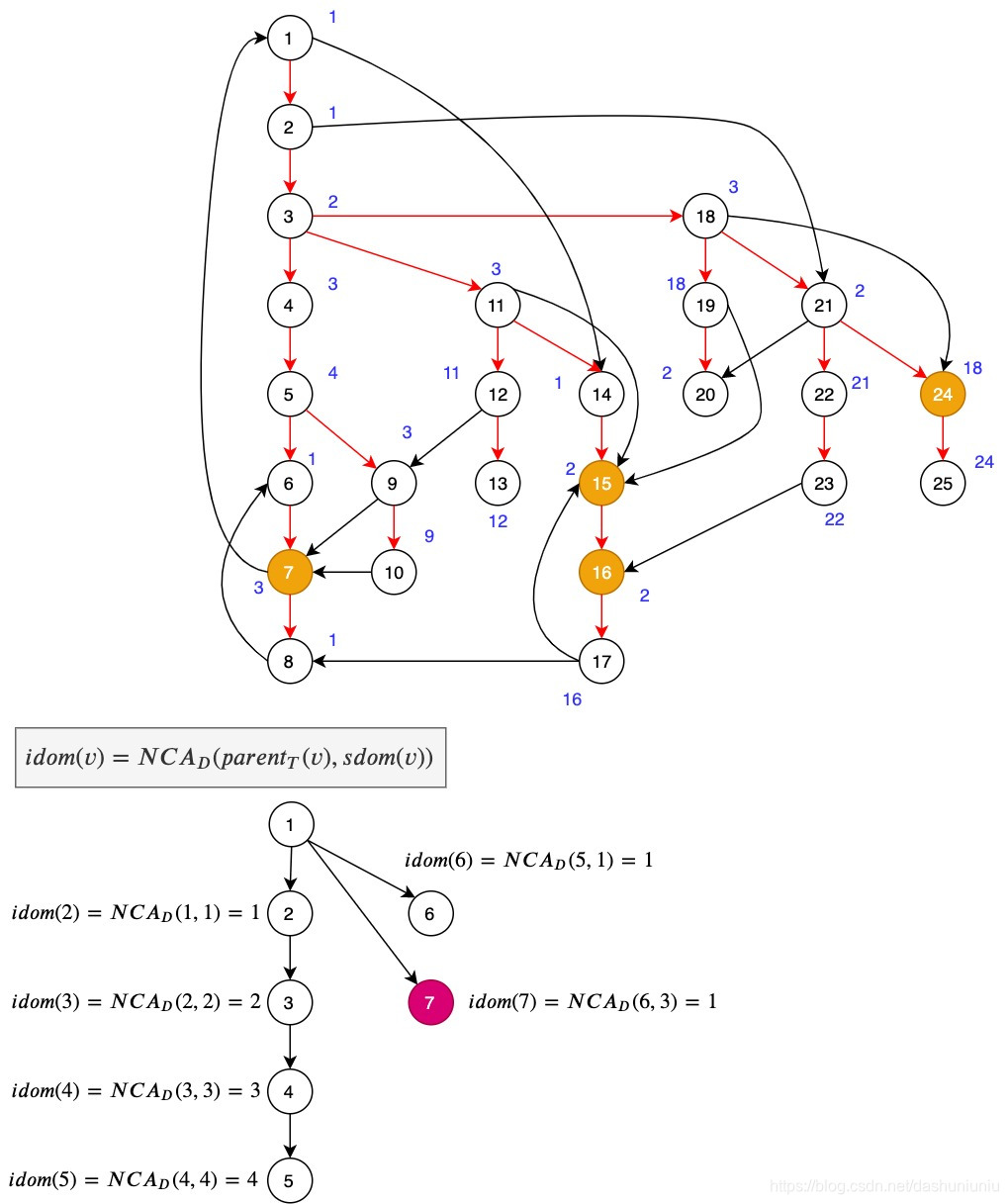
Lemma 1: For any vertex $v\ne s$ is the nearest common ancestor in $D$ for $sdom(v)$ and $paren{t}_T(v)$:

$$idom(v)=NC{A}_D(paren{t}_T(v),sdom(v))$$

如上图中的$7$，$sdom(7)=3$，那么$idom(7)=NC{A}_D(6,3)=1$。

整个算法过程如下图所示：

注：上图算法来自于Algorithms for Finding Dominators in Directed Graphs

我们可以看到SEMI-NCA比原始的LT算法好理解多了。llvm在2017年将LT算法替换为SEMI-NCA算法，具体的实现细节见视频《2017 LLVM Developers’ Meeting: J. Kuderski “Dominator Trees and incremental updates that transcend time》介绍了开发人员在应用SEMI-NCA算法时的方方面面。

当然dominator算法还有很多可以挖掘的细节，但是semi-nca算法看起来是当前比较稳定的最优选择的算法。

论文列表

1. Algorithms for Finding Dominators in Directed Graphs
2. https://renatowerneck.files.wordpress.com/2016/06/gwtta04-dominators.pdf
3. https://www.cs.princeton.edu/courses/archive/fall03/cs528/handouts/a%20fast%20algorithm%20for%20finding.pdf
4. https://www.cs.princeton.edu/courses/archive/spr11/cos423/Lectures/DominatorsA.pdf
5. https://www.doc.ic.ac.uk/~livshits/classes/CO444H/reading/dom14.pdf
6. Finding dominators revisited: Extended abstract
7. Linear-Time Algorithms for Dominators and Related Problems

其中Loukas的《Linear-Time Algorithms for Dominators and Related Problems》和《Algorithms for Finding Dominators in Directed Graphs》的描述比较完整。