AI（004） - 笔记 - 模型评估与选择

模型评估与选择

这篇文章是学习了2周后，对模型评估与选择的总结，对应：

• 第一周：（04）1.4 机器学习算法的组成部分
• 第一周：（08）1.6 线性回归模型——模型选择
• 第二周：（04）2.4 不平衡数据分类学习
• 第二周：（05）2.5 分类模型的评价
• 《机器学习》（西瓜书）：第2章 模型评估与选择
• 维基百科（en）：“Precision and recall” 词条
• 维基百科（en）：“Receiver operating characteristic” 词条
• 维基百科（en）：“F1 score” 词条

文章标题排版以西瓜书为参考。另外公式比较多，app会乱码。请在浏览器或电脑查看。

---

---

1 经验误差（empirical error）与过拟合（overfitting）

• 错误率（error rate）：错误的样本数占样本总数的比例。

  即在m个样本中有a个样本分类错误，则：

  • 错误率（errpr rate）: E = a / m
  • 精度（accuracy）：1 - a / m

• 误差（error）：实际预测输出与样本的真实输出之间的差异。

  • 训练误差（training error）或经验误差（empirical error）：训练集（training set）上的误差。

  • 泛化误差（generalization error）：新样本上的误差。

• 过拟合（overfitting）：把训练样本自身的一些特点当成所有潜在样本都会具有的一般性质，导致泛化性能下降。

• 欠拟合（underfitting）：对训练样本的一般性质尚未学好。

---

2 评估方法（evaluation）

要评估，需使用一个“测试集”（testing set）来测试学习器对新样本的判别能力，然后以测试集上的“测试误差”（testing error）作为泛化误差的近似。

测试集应尽可能与训练集互斥。

假定，一个包含m个样例的数据集D，从中产生训练集S和测试集T，则：

2.1 留出法（hold-out）

留出法：直接将数据集D分割成两个互斥集合，即：

$$D = S \bigcup T, \quad S \bigcap T = \emptyset$$

分层采样（stratified sampling）：保留类别比例的采样方式。

单次使用留出法得到的估计结果往往不够稳定可靠，在使用留出法时，一把要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的结果。

留出法的问题：

• 如果S较大，结果可能不够稳定准确；

• 如果S较小，会降低评估结果的保真性（fidelity）。

这个问题没有完美的解决方案，常见做法是将大约 2/3 ~ 4/5 的样本用于训练。

2.2 k折交叉验证法（k-fold cross validation）

k折交叉验证法：将D分割成k个大小相似的互斥子集，即：

$$D = D_1 \bigcup D_2 \bigcup \ldots \bigcup D_k, \quad D_i \bigcap D_j = \emptyset \; (i \neq j)$$

然后，每次用k-1个子集的并集作为训练集，余下的子集作为测试集；进行k次训练和测试，最终返回k个测试结果的均值。

常见k的取值：5，10，20等

为减少因样本划分不同而引入的差别，k折交叉验证通常要随机使用不同的划分重复p次，最终评估结果是p次k折交叉验证结果的均值。

当 k = m 时，称为留一法（Leave-One-Out，简称LOO）。留一法评估结果往往被认为比较准确，但当D比较大时，开销可能是难以忍受的。

2.3 自助法（bootstrapping）

自助法：以自助采样（bootstrap sampling）为基础产生数据集，即随机从D中选择一个样本的拷贝，重复m次，作为训练集。不被采样到的概率再取极限得

$$\lim_{m \to \infty} \left( 1 - \frac{1}{m} \right)^m = \frac{1}{e} \approx 0.368$$

即，约有36.8%未被采样，并将它作为测试集。这样产生的测试结果称为“包外估计”（out-of-bagestimate）。

由于自助法产生的数据集改变了初始数据集的分布，这会引入估计误差。因此，当数据量足够时，留出法与交叉验证法更常用。

2.4 调参（parameter tuning）与最终模型

• 对每种参数配置都训练出模型是不可行的。常见做法，对每个参数选定一个范围和变化步长。

• 在模型选择完成后，学习算法和参数配置已选定，此时应该用D重新训练。

• 模型评估与选择中用于评估测试的数据集常称为“验证集”（validation set）。

---

3 性能度量（performance measure）

性能度量：衡量模型泛化能力的评价指标。学习器记作$f$。

• 最常用的指标是均方误差（mean squared error）：

  $$E(f; D) = \frac{1}{m} \sum_{i = 1}^{m} (f({\bf x}_i) - y_i)^2$$

  • 对于数据分布D与概率密度函数p(·)，均方误差为：

    $$E(f; {\mathcal D}) = \int_{{\bf x} \sim {\mathcal D}} (f({\bf x}) - y)^2 p({\bf x}) d{\bf x}$$

  • 3.1 错误率（error rate）与精度（accuracy）

    一般的

    • 错误率（error rate）

      $$E(f; D) = \frac{1}{m} \sum_{i = 1}^{m} {\Bbb I} (f({\bf x}_i) \neq y_i)$$

    • 精度（accuracy）：

      $$acc(f; D) = \frac{1}{m} \sum_{i = 1}^{m} {\Bbb I} (f({\bf x}_i) = y_i) = 1 - E(f; D)$$

    对于数据分布D与概率密度函数p(·)，有

    • 错误率（error rate）

      $$E(f; {\mathcal D}) = \int_{{\bf x} \sim {\mathcal D}} {\Bbb I} (f({\bf x}) \neq y) p({\bf x}) d{\bf x}$$

    • 精度（accuracy）：

      $$acc(f; {\mathcal D}) = \int_{{\bf x} \sim {\mathcal D}} {\Bbb I} (f({\bf x}) = y) p({\bf x}) d{\bf x} = 1 - E(f; {\mathcal D})$$

    3.2 查准率（precision）、查全率（recall）与F1分数（F1 score）

    对于二分类问题（binary classification）可将样例（example）根据其真实性类别与学习器预测类别的组合划分为：

    • 真正例（true positive，TP）
    • 假正例（false positive，FP）
    • 真反例（true negative，TN）
    • 假反例（false negative，FN）

    显然有 TP + FP + TN + FN = 样例总数。

    混淆矩阵（confusion matrix）为：

    $$\begin{array}{c|ccc} & \hat{y} = 1 & \hat{y} = 0 & \sum \\[2ex] y = 1 & TP & FN & N_+ \\[2ex] y = 0 & TN & FP & N_- \\[2ex] \sum & \hat{N}_+ & \hat{N}_- & \end{array}$$

    查准率（precision）又叫准确率，查准率P：

    $$P = \frac{TP}{TP + FP}$$

    查全率（recall）又叫召回率，查全率R：

    $$R = \frac{TP}{TP + FN}$$

    3.2.1 P-R曲线（Precision and Recall Curve）

    将学习器的预测结果进行排序（最可能-最不可能），把样本作为正例进行预测，则每次可以计算出查准率和查全率。然后生成的查准率-查全率曲线即P-R曲线。

    

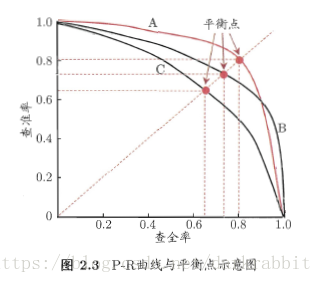
    图片出自（《机器学习》——周志华）。

    • 若一个学习器的P-R曲线被另一个完全“包住”，则后者优于前者，即A优于C；
    • 若两个曲线发生交叉，“平衡点”（Break-Even Point，简称BEP）大的优于小的，即A优于B。‘’

    3.2.2 F1 score

    由于BEP还是过于简化了，更常用的是F1度量。

    $$F1 = \frac{2 \times P \times R}{P + R} = \frac{2 \times TP}{\text{样例总数 + TP - TN}}$$

    F1度量的一般形式——$F_\beta$，能表达出对查准率/查全率的不同偏好，它定义为：

    $$F_\beta = \frac {(1 + \beta^2) \times P \times R} {(\beta^2 \times P) + R}$$
    • $\beta > 0$度量了R对P的相对重要性；
    • $\beta = 1$时，退化为标准的F1；
    • $\beta > 1$时，R有更大影响；
    • $\beta < 1$时，P有更大影响。

    F1是基于查准率与查全率的调和平均（harmonic mean）定义的：

    $$\frac{1}{F1} = \frac{1}{2} \cdot \left( \frac{1}{P} + \frac{1}{R} \right)$$

    而$F_\beta$则是加权调和平均：

    $$\frac{1}{F_\beta} = \frac{1}{1 + \beta^2} \cdot \left( \frac{1}{P} + \frac{\beta^2}{R} \right)$$

    Wiki对于F1的原文：

    The traditional F-measure or balanced F-score (F1 score) is the harmonic mean of precision and recall:
    

    $$F_1 = \frac{2}{ \frac{1}{recall} + \frac{1}{precision} } = 2 \cdot \frac{precision \cdot recall}{precision + recall}$$

    The general formula for positive real $\beta$ is:
    

    $$F_\beta = (1 + \beta^2) \cdot \frac{precision \cdot recall}{(\beta^2 + precisioon) + recall}$$

    The formula in terms of Type I and type II errors:
    

    $$F_\beta = \frac { (1 + \beta^2) \cdot true \, positive } { (1 + \beta^2) \cdot true \, positive + \beta^2 \cdot false \, negative + false \, positive }$$

    Two other commonly used $F$ measures are the $F_2$ measure, which weighs recall higher than precision (by placing more emphasis on false negatives), and the $F_{0.5}$ measure, which weighs recall lower than precision (by attenuating the influence of false negatives).

    The F-measure was derived so that $F_{\beta}$ “measures the effectiveness of retrieval with respect to a user who attaches β times as much importance to recall as precision”. It is based on Van Rijsbergen’s effectiveness measure.
    

    $$E = 1 - \left( \frac{\alpha}{p} + \frac{1 - \alpha}{r} \right)^{-1}$$

    Their relationship is $F_\beta = 1 - E \quad where \quad \alpha = \frac{1}{1 + \beta^2}$

    The F1 score is also known as the Sørensen–Dice coefficient or Dice similarity coefficient (DSC).

    3.2.3 n个二分类混淆矩阵的F1

    在n个二分类混淆矩阵上综合考察查准率和查全率。有两种方法：

    • 其一：宏查准率（macro-P），宏查全率（macro-R），宏F1（macro-F1）

      $$macroP = \frac{1}{n} \sum_{i = 1}^{n} P_i$$
      $$macroR = \frac{1}{n} \sum_{i = 1}^{n} R_i$$
      $$macroF1 = \frac{2 \times macroP \times macroR}{macroP + macroR}$$

    • 其二：微查准率（micro-P），微查全率（micro-R），微F1（micro-F1）

      $$microP = \frac{\overline{TP}}{\overline{TP} + \overline{FP}}$$
      $$microR = \frac{\overline{TP}}{\overline{TP} + \overline{FN}}$$
      $$microF1 = \frac{2 \times microP \times microR}{microP + microR}$$

    3.3 ROC（Receiver Operating Characteristic）与AUC（Area Under ROC Curve）

    ROC曲线：根据预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个值

    • 真正例率（True Positive Rate，简称TPR），纵轴

      $$TPR = \frac{TP}{TP + FN}$$

    • 假正例率（False Positive Rate，简称FPR），横轴

      $$FPR = \frac{FP}{TN + FP}$$

    组成的图像。

    

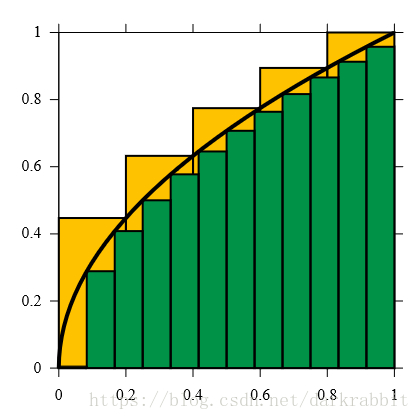
    图片出自（维基百科——Receiver Operating Characteristic词条）。

    • 若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”，则后者性能优于前者；
    • 若发生交叉，则比较ROC曲线下的面积，即AUC（Area Under ROC Curve，绿色部分）。

    AUC的估计为：

    $$AUC = \frac{1}{2} \sum_{i = 1}^{m - 1} (x_{i + 1} - x_i) \cdot (y_i + y_{i + 1})$$

    排序损失（loss）为：

    $$\ell_{rank} = \frac{1}{m^+ m^-} \sum_{x^+ \in D^+} \sum_{x^- \in D^-} \left( {\mathbb I} (f(x^+) < f(x^-)) + \frac{1}{2} {\mathbb I}(f(x^+) = f(x^-)) \right)$$

    其中$m^+, m^-, D^+, D^-$为正例，反例，正例集合，反例集合。

    则

    $$AUC = 1 - \ell_{rank}$$

    3.4 代价敏感学习

    在算法层面上解决不平衡数据学习的方法主要是基于代价敏感学习算法（Cost-Sensitive Learning）

    代价敏感学习方法的核心要素是代价矩阵（cost matrix）：不同类型的误分类情况导致的代价不一样：

    $$\begin{array}{c|cc} Predict \backslash True & 0 & 1 \\[2ex] 0 & C_{00} & C_{01} \\[2ex] 1 & C_{10} & C_{11} \end{array}$$

    基于代价矩阵分析，代价敏感学习方法主要有以下方法：

    • 从贝叶斯风险理论出发，把代价敏感学习堪称是分类结果的一种后处理，按照传统方法学习到一个模型，以实现损失最小为目标对结果进行调整
      
      • 不依赖所用具体的分类器
      • 但是缺点要求分类器输出值为概率
    • 从学习模型出发，对具体学习方法的改造，使之能适应不平衡数据下的学习
      
      • 代价敏感的支持向量机，决策树，神经网络
      • 预处理的角度出发，将代价用于权重的调整，使得分类器满足代价敏感的特性