深入理解opengl坐标系统

内容参考songho.ca/opengl、learnopengl

坐标变换流程

坐标变换主要发生在顶点处理阶段，外加光栅化进行一次视口变换

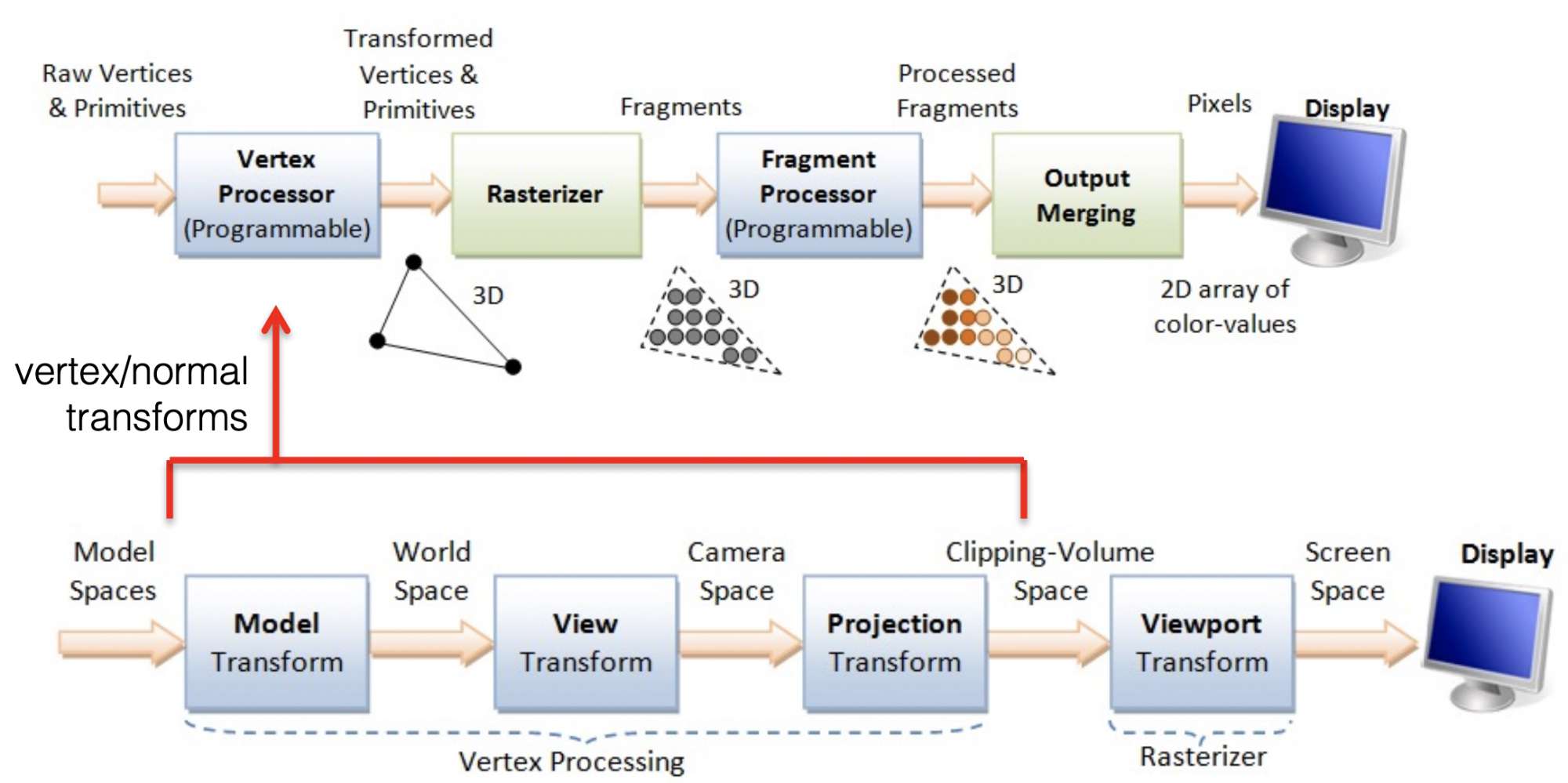
各个阶段变换说明：

1. Model 变换，指模型本身的调整，比如一个人物模型，建模的时候原点放在腰上，放到场景中，一半在平面坐标系下面了，要把脚和地平面对齐，Model变换加一个向上的平移
2. VIEW 变换，opengl本身没有相机的概念，场景视角默认冲着屏幕里，即-z轴。相机的变换是通过对场景做逆变换实现的，比如相机旋转30°，则实际是将场景旋转-30°
3. Projection 变换，空间中的坐标最后都要在二维的平面上绘制，Projection就是将3D的坐标变换到2D(不太准确，下面会深入projection原理)

看下图，3.View Space到4.CLIP SPACE的区别，经过透视投影到剪裁空间后，物体符合近大远小的视觉效果，立方体背面的xy坐标变小了，更靠近原点，右边锥体的尖儿也相对的远离原点了(尖儿更靠前)

整个渲染过程涉及5个坐标系，坐标范围如下，参考下图

坐标系	坐标范围	说明
Object/Local Coordinate	[-∞， +∞]	空间任意值
Eye/View Coordinate	[-∞， +∞]	空间任意值
Clip Coordinate	[-∞， +∞]	x、y在近平面的宽高范围内
NDC coordinate	[-1， +1]	投影变换之后，除以齐次坐标W得到
Screen Space	[0， 宽/高]	窗口宽高范围内

注：opengl是右手坐标系，拇指、食指、中指分别指向x、y、z轴正方向

注，Divide by w这一步是opengl管线自己做的，开发者只要按要求计算好齐次坐标的w值。

齐次坐标理解参考：Homogeneous Coordinates

model view projection变换，我们一般简称为mvp变换，mv相对简单，重点看看projection变换实现

投影矩阵

投影分两种：

• 透视投影(Perspective Projection)，会渲染成近大远小
• 正交投影(Orthographic Projection)，长宽按照1:1渲染，不会缩放

正常情况下，场景的渲染使用透视投影，一些特殊的场景会选择正交投影，比如游戏中人物的血条，平行光的阴影图(shadow map)

projection变换后得到clip space坐标P($x_c,y_c,z_c,w_c$)

opengl管线会根据clip坐标进行剪裁，在camera视锥范围外的顶点会被丢弃，判断计算：

如果出现裁剪，OpenGL会在网格的裁剪处进行重建

透视投影(Perspective Projection)

透视变换中，假设人眼/相机看到的是一个被裁剪的金字塔锥体，3D坐标投影变换后，映射到单位立方体空间内[-1, 1]，

• x轴范围[l, r] ==> [-1, 1]
• y轴范围[b, t] ==> [-1, 1]
• z轴范围[-n, -f]==> [-1, 1]

右手坐标系下，camera看向-z方向，这里n、f > 0，所以前面加负号

理解透视变换的关键在于，要凑出一个矩阵，使得点$(x_{eye},y_{eye},z_{eye},w_{eye})$ 左乘矩阵$M_{projection}$后得到一个齐次坐标$(x_{clip},y_{clip},z_{clip},w_{clip})$，之后$(x_{clip},y_{clip},z_{clip},w_{clip})/w_{clip}$ 要得到NDC空间坐标，即xyz/w后能归一化到[-1, 1]范围

1. 设 $w_{clip}=z_{eye}$，这个设定是合理的(我觉得也可以设定成其他的合理值，只要和z坐标相关成比例，符合人眼视觉成像的效果即可)

$w_{clip}$ 由矩阵M的第四行决定的

2. 由3D空间 到 NDC空间映射关系推导出矩阵上面三行的数值

OpenGL中，3D空间中的点投影到近平面.

下图展示eye space中的点$(x_e,y_e,z_e)$ 投影到近平面的坐标为$(x_p,y_p,z_p)$

从top视角看，根据相似三角形可得：

从侧视角看，得到y坐标的比例关系

按线性关系，建立投影坐标到NDC空间坐标的变换(l, r)=>(-1, 1), (b, t)=>(-1, 1)，clip坐标经过一次缩放和一次平移得到NDC 坐标。

则$x_{ndc}$坐标

同理可得到$y_{ndc}$坐标

整个过程按 eye space ==> clip space ==> ndc space流程建立方程，基于齐次坐标和NDC坐标范围约束建立方程。

替换上面方程的$x_p$ 和$y_p$，经过变形将$-z_e$提取到分母中

前面已经设$w_c=-z_e$，所以括号内的项就是clip空间的$x_c、y_c$坐标，则可得到投影矩阵的第一行和第二行

3. 求投影矩阵第三行数值

$z_c$和x、y没关系，只可能和 z w项有关，设这两项对应的矩阵系数为A B

设定eye space中的$w_e$为1，上图右边的等式为

利用$z_e$ ==> $z_n$的映射关系 clip space(-n, -f) ==> NDC space(-1, 1)，得到：

得到B：

得A:

A代入到B得：

则得到$z_n$为：

则，推断矩阵的第三行为：

上面是通用的投影矩阵，如果视锥是对称的，即r = -l, t = - b，则该矩阵可以简化为：

注意:
投影矩阵之后需要除以w项，才能得到NDC空间坐标(-1, 1)，w = z。则从z_clip 到 z_ndc，是一个类似 f(z) = 1/-z 的函数，

可以看到，这个映射不是均匀的，在远平面变化比较慢。则远处的点映射到ndc空间，深度值比较接近，渲染时由于深度值不精确，会产生z-fight现象，远处的挨在一起的面片可能会闪烁。

正交投影(Orthographic Projection)

正交投影相对简单多了，长方体的视锥缩放到单位正方体，再平移到原点

不需要经过clip space坐标中转了，直接由eye space 变换到NDC空间，对比结果凑出正交矩阵数值。当然，还是需要按缩放+平移的思路，分别凑出x、y、z坐标的方程。

注意，正交投影xy坐标是1:1变换到近平面的，所以不需要去凑w项了。

参考透视投影流程

则，对应的矩阵为

如果该正交矩阵是对称的，即r = -l, t = -b，则可以进一步简化矩阵

投影矩阵不是本来就存在的科学原理，是工程上能自圆其说的一种假设的模型，我感觉就是凑出来这个矩阵，好使就行。