二维旋转变换

求点 P(x1, y1) 绕点 Q(x2, y2) 逆时针旋转 θ 得到的点的坐标

先看绕原点旋转的情况：

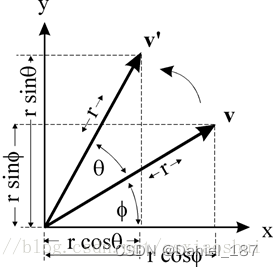
如图所示点 v 绕 原点旋转 θ 角，得到点v’，假设 v点的坐标是(x, y) ，那么可以推导得到 v’点的坐标（x’, y’)：

$$\{\begin{array}{rl}x& =r\ast \cos \theta \\ y& =r\ast \sin \theta \end{array}$$

$$\{\begin{array}{rl}{x}^{\prime }& =r\ast \cos (\varphi +\theta )\\ y^{\prime }& =r\ast \sin (\varphi +\theta )\end{array}$$

展开得：

$$\{\begin{array}{rl}{x}^{\prime }& =r\ast \cos \varphi \ast \cos \theta -r\ast \sin \varphi \ast \sin \theta \\ y^{\prime }& =r\ast \sin \varphi \ast \cos \theta +r\ast \cos \varphi \ast \sin \theta \end{array}$$

带入 x 和 y 的表达式：

$$\{\begin{array}{rl}{x}^{\prime }& =x\ast \cos \theta -y\ast \sin \theta \\ y^{\prime }& =y\ast \cos \theta +x\ast \sin \theta \end{array}$$

写为矩阵：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\ast \left[\begin{array}{c}x\\ y\end{array}\right]$$

于是我们得到旋转变换矩阵 M：

$$M=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$

设旋转后的到的坐标为 P’(x’, y’)，类似于平面向量中将起点平移至原点的思想，我们可以将 P 点绕 Q 点旋转的过程看作 QP 向量旋转得到 QP’ 向量，于是根据 P 和 Q 坐标有：

$$\left[\begin{array}{c}{x}^{\prime }-x_2\\ y^{\prime }-y_2\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\ast \left[\begin{array}{c}{x}_1-x_2\\ y_1-y_2\end{array}\right]$$

于是得到 P’ 坐标为：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\ast \left[\begin{array}{c}{x}_1-x_2\\ y_1-y_2\end{array}\right]+\left[\begin{array}{c}{x}_2\\ y_2\end{array}\right]$$

算法实现：

from collections import namedtuple
import math

Point = namedtuple("Point", ["x", 'y'])


def matrix_mul(M: list[list[float]], vec: list[float]) -> list[float]:
    res = []
    for row in M:
        res.append(sum([a * b for (a, b) in zip(row, vec)]))
    return res


def rotate(p: Point, q: Point, theta: float) -> Point:
    M = [
        [math.cos(theta), -math.sin(theta)],
        [math.sin(theta), math.cos(theta)]
    ]
    pq = [p.x - q.x, p.y - q.y]
    t = matrix_mul(M, pq)
    t[0] += q.x
    t[1] += q.y
    return Point(t[0], t[1])


def main():
    print(rotate(Point(1.414, 0), Point(0, 0), math.pi / 4), "expect (1, 1)")
    print(rotate(Point(1, 1), Point(0, 0), -math.pi / 4), "expect (1.414, 0)")
    print(rotate(Point(2, 2), Point(1, 1), -math.pi / 4), "expect (2.414, 1)")


if __name__ == '__main__':
    main()