Preface
主要内容:
Bayesian Statistics And Regularization(贝叶斯统计和规则化)
Maximum A Posteriori(最大后验概率估计)
Bayesian Statistics And Regularization
在这里我们将使用一种不同于最大似然估计的方法来求解
h(θ)
h
(
θ
)
中的
θ
θ
。(换句话说,就是要找到一种更好的估计方法来减小过拟合的问题)
在最大似然估计方法我们将
θ
θ
看成未知常数,但是在别外的一种方法——贝叶斯方法中将
θ
θ
看成未知随机变量,这样一来我们使用先验分布
p(θ)
p
(
θ
)
来表示
θ
θ
最可能的值。
当我们需要对基于给定的数据集
S={(x(i),y(i))}mi=1
S
=
{
(
x
(
i
)
,
y
(
i
)
)
}
i
=
1
m
,给出未知
x
x
的预测值时,我们就可以使用贝叶斯方法来计算 的后验分布。
1.对于上述公式的理解:
由于
S
S
表示的是样本集,所以由 预测
y
y
的 对应到公式中由:
在 p(S) p ( S ) 推导的第三步出现 θ θ 表示的是数据集 S={(x(i),y(i))}mi=1 S = { ( x ( i ) , y ( i ) ) } i = 1 m 在先验分布参数 θ θ 的作用下,再来给出未知 x x 的预测值。
由于 与 p(S) p ( S ) 中都有 p(x(i)) p ( x ( i ) ) 分子分母同时约去就可以得到我们最先的推导。
2.同时对于上述公式中的
p(y(i)|x(i),θ))p(θ)
p
(
y
(
i
)
|
x
(
i
)
,
θ
)
)
p
(
θ
)
是由我们选择的模型给定的。
例如:贝叶斯 logistic 回归。
3.所以在
θ
θ
看成未知随机变量的情况下,对于
x
x
的预测的后验分布为:
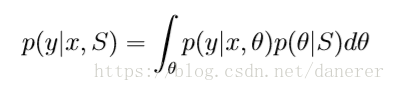
所以,它的期望为:
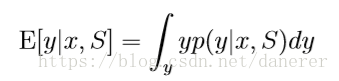
Maximum A Posteriori
大多数时候我们只需求得 中最大值即可。
然而在贝叶斯估计方法中,虽然公式合理优美,但后验概率p(θ|S)很难计算,看其 公式知道计算分母时需要在所有的θ上作积分,然而对于一个高维的θ来说,枚举其所有的 可能性太难了。 为了解决这个问题,我们需要改变思路。看p(θ|S)公式中的分母,分母其实就是 P(S), 而我们就是要让 P(S)在各种参数的影响下能够最大(这里只有参数θ)。因此我们只需求出随 机变量θ中最可能的取值,这样求出θ后,可将θ视为固定值,那么预测时就不用积分了,而 是直接像最大似然估计中求出θ后一样进行预测,这样就变成了点估计。这种方法称为最大后验概率估计(Maximum a posteriori)方法。
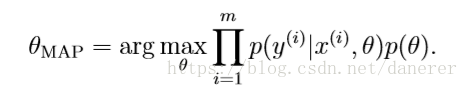







 本文探讨了贝叶斯统计中的规则化方法及其如何通过引入先验分布来改进参数估计,避免过拟合问题。同时介绍了最大后验概率估计方法,这是一种在贝叶斯框架下寻找最有可能参数值的技术。
本文探讨了贝叶斯统计中的规则化方法及其如何通过引入先验分布来改进参数估计,避免过拟合问题。同时介绍了最大后验概率估计方法,这是一种在贝叶斯框架下寻找最有可能参数值的技术。
















 2837
2837

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








