2023.11Datewhale_Leedcode_基础数据结构篇（下）学习笔记（一）

已于 2023-11-22 09:26:14 修改
阅读量144 收藏
点赞数
文章标签： 数据结构 笔记 python leetcode 散列表 算法
于 2023-11-15 00:15:04 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/dandellion_/article/details/134410642
版权

一、哈希表

1. 存在重复元素

描述：给定一个整数数组 nums。

要求：判断是否存在重复元素。如果有元素在数组中出现至少两次，返回 True；否则返回 False。

说明：

  • 1≤nums.length≤10e5。
  • −10e9≤nums[i]≤10e9。
class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        return len(nums) != len(set(nums))

        先集合排重，再检验是否有损失长度，判定结果即为布尔值。（一开始我居然遍历数组把元素加入空集合，结局是超时）

class Solution:
    def containsDuplicate(self, nums: List[int]) -> bool:
        # 初始化字典
        d = dict()
        # 遍历数组
        for i in range(0,len(nums)):
            # 无相同键
            if nums[i] not in d:
                d[nums[i]]=i
            # 有相同键
            else:
                return True
        return False

        （然后想起来我在学哈希表，所以用字典又做了一次）把数组元素添加到字典前，查询一下字典里是否已经存在该元素。

2. 存在重复元素 II

描述：给定一个整数数组 nums 和一个整数 k。

要求：判断是否存在 nums[i] == nums[j](i≠j) 且 abs(i - j) <= k ，并且 i 和 j 的差绝对值至多为 k。

说明：

  • 1 <= nums.length <= 10e5
  • -10e9 <= nums[i] <= 10e9
  • 0 <= k <= 10e5
class Solution:
    def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:
        # 初始化字典
        d = dict()
        # 遍历数组
        for i in range(0,len(nums)):
            # 各键不同，直接加入字典
            if nums[i] not in d:
                d[nums[i]]=i
            # 有相同键
            else:
                # 索引差绝对值判定
                if abs(i - d[nums[i]]) <= k:
                    return True
                # 删除原重复键，再加入字典
                else:
                    del d[nums[i]]
                    d[nums[i]]=i
        return False

         与上题相比，这题增加了对索引差绝对值的判定。由于判定标准是对最小差的限制，所以只需求邻近相同元素的索引差，为防止哈希冲突，将一个元素加入字典前，需要删除字典中已存在的相同元素。

3. 有效的数独

描述：给定一个数独，用 9 * 9 的二维字符数组 board 来表示，其中，未填入的空白用 "." 代替。

要求：判断该数独是否是一个有效的数独。

说明：

  • 一个有效的数独（部分已被填充）不一定是可解的。
  • 只需要根据以上规则，验证已经填入的数字是否有效即可。
  • 空白格用 '.' 表示。

一个有效的数独需满足：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3 * 3 宫内只能出现一次。（请参考示例图）

示例：

class Solution:
    def isValidSudoku(self, board: List[List[str]]) -> bool:

        # 子块左上角索引
        q = [0,3,6]

        # 逐行检查重复元素
        for i in range(0,9):
            # 换行时初始化字典
            d = dict()
            for j in range(0,9):
                # 跳过空值
                if board[i][j]=='.':
                    continue
                elif board[i][j] not in d:
                    # 哈希函数为列索引值
                    d[board[i][j]]=j
                else:
                    return False

        # 逐列检查重复元素
        for j in range(0,9):
            d = dict()
            for i in range(0,9):
                if board[i][j]=='.':
                    continue
                elif board[i][j] not in d:
                    d[board[i][j]]=i
                else:
                    return False

        # 逐子块检查重复元素
        for ip in q:
            for jp in q:
                # 换块初始化
                d = dict()
                # 块内行列遍历
                for i in range(0,3):
                    for j in range(0,3):
                        if board[ip+i][jp+j]=='.':
                            continue
                        elif board[ip+i][jp+j] not in d:
                            # 哈希函数为表值
                            d[board[ip+i][jp+j]]=board[ip+i][jp+j]
                        else:
                            return False

        return True

         根据前两题的方法，分别对各行各列和九个子块进行重复元素检测。

class Solution:
    def isValidSudoku(self, board: List[List[str]]) -> bool:

        # 初始化9*9二维数组，存储三个哈希表的哈希值
        # 分别用于判定行、列和九个子块是否存在重复元素
        row = [[0] * 9 for _ in range(9)]
        col = [[0] * 9 for _ in range(9)]
        block = [[0] * 9 for _ in range(9)]
        
        #遍历整个9*9数独表
        for i in range(9):
            for j in range(9):
                # 跳过空值
                if board[i][j] != '.':
                    # 建立哈希函数
                    num = int(board[i][j]) - 1
                    # 计算所在子块序号
                    b = (i // 3) * 3 + j // 3
                    # 检测是否存在哈希冲突
                    if row[i][num] or col[j][num] or block[b][num]:
                        return False
                    # 模拟存储
                    row[i][num] = col[j][num] = block[b][num] = 1
        return True

上个解法显然不够哈希。于是换了一个思路：

        把数独表中每个元素的值映射到二维数组的一个索引，二维数组的另一个索引与该元素的行索引或列索引相同，让元素的值和位置与二维数组中的空间区域同时产生联系。

        二维数组中，1代表存储占用，0代表空余空间，录入前确定元素在三个二维数组里都有剩余空间后，然后再存储进去。

        这样的话，数独表中如果存在同行列或同子块的同值元素，就会对应到二维数组的相同区域，即产生了哈希冲突，从而判断同值函数。

那么问题来了，如何让元素的所在子块的位置与数组索引建立联系呢？

        可以将9个子块从左到右、从上到下依次从0到8编号。先看第一行子块。

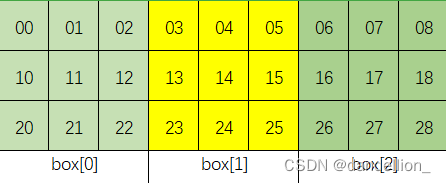
        容易发现，仅需对元素的列索引整除3即可得到子块索引，即 index(box) = j // 3 。当这个问题拓展到3行子块时，需要在这个基础上加一个3的倍数，这个倍数就是 i // 3 。

        从而 b = (i // 3) * 3 + j // 3 。

ps. 简化变量名称，删掉注释会让评价更高一点，但我毕竟是写笔记，成绩图片是我在这个思路下尝试的能跑出的最好结果。

4. 两个数组的交集

描述：给定两个数组 nums1 和 nums2。

要求：返回两个数组的交集。重复元素只计算一次。不考虑输出结果的顺序。

说明：

  • 1 <= nums1.length, nums2.length <= 1000

  • 0 <= nums1[i], nums2[i] <= 1000

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        return list(set(nums1) & set(nums2))

         set哈希，暴力求解（既然不管顺序，那就别怪我不讲武德）。

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        a = [0] * 1001
        b = [0] * 1001
        for i in nums1:
           a[i] += 1
        for j in nums2:
           b[j] += 1
        r = []
        for i in range(1001):
            if a[i] * b[i] >0:
                r.append(i)
        return r

        （还是讲点吧）把值映射到空间，输出相同位置的元素，需要注意的是，应根据提示给出的范围规定数组哈希表的长度。

5. 两个数组的交集 II

描述：给定两个数组 nums1 和 nums2。

要求：返回两个数组的交集。可以不考虑输出结果的顺序。

说明：

  • 输出结果中，每个元素出现的次数，应该与元素在两个数组中都出现的次数一致（如果出现次数不一致，则考虑取较小值）。
  • 1 <= nums1.length, nums2.length <= 1000
  • 0 <= nums1[i], nums2[i] <= 1000
class Solution:
    def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
        a = [0] * 1001
        b = [0] * 1001
        for i in nums1:
           a[i] += 1
        for j in nums2:
           b[j] += 1
        nums1 = []
        for i in range(1001):
            if a[i] and b[i]:
                nums1 += [i]*min(a[i],b[i])
        return nums1

与上题思路大体相同，细节处有所改动：

  • 回收了遍历后的无用数组变量，用于储存结果；
  • 不用乘积是否为0判断哈希冲突，直接对值进行 and 逻辑运算判断；
  • 取重复元素的最小出现次数，倍加入结果数组。

class Solution:
    def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
      return list((Counter(nums1) & Counter(nums2)).elements())

         还有一种省心的思路：调用Counter类的Counter方法和elements方法。前者返回一个键为元素，值为出现次数的字典；后者将元素按照对应次数返回。

6. 设计哈希映射

要求：不使用任何内建的哈希表库设计一个哈希映射（HashMap）。

需要满足以下操作：

  • MyHashMap() 用空映射初始化对象。
  • void put(int key, int value) 向 HashMap 插入一个键值对 (key, value) 。如果 key 已经存在于映射中，则更新其对应的值 value。
  • int get(int key) 返回特定的 key 所映射的 value；如果映射中不包含 key 的映射，返回 -1。
  • void remove(key) 如果映射中存在 key 的映射，则移除 key 和它所对应的 value 。

说明：

  • 0 <= key, value <= 10e6
  • 最多调用 10e4 次 put、get 和 remove 方法
class MyHashMap:
    # 初始化无参数实例对象，即用空映射初始化对象
    def __init__(self):
        # 初始化一个索引范围与key的值域相同的一维数组
        self.l = [-1 for _ in range(1000001)]

    # 定义存储方法：hash(key) = key, value -> hash_map[hash(key)]
    def put(self, key: int, value: int) -> None:
        self.l[key] = value

    # 定义查找方法
    def get(self, key: int) -> int:
        return self.l[key]

    # 定义删除方法：将对应位置存储的值修改为空值
    def remove(self, key: int) -> None:
        self.l[key] = -1

         简单的哈希函数完全防止了哈希冲突，但是代价是开辟的极长数组空间占用了过多内存，而实际应用中，这些空间是冗余的。

class MyHashMap:

    def __init__(self):
        # 开辟一个大数组，长度为质数，注意 [[]*20011] == [[]]
        # 一般定义成离2的整次幂比较远的质数，这样取模之后冲突的概率比较低。
        self.hash = [[] for _ in range(20011)]  


    def put(self, key: int, value: int) -> None:
        t = key % 20011
        # 遍历哈希到的链表中，查找key,并更新值
        for item in self.hash[t]:  
            if item[0] == key:
                item[1] = value
                return  # 更新完之后，直接返回 None（可略）
        # 如果链表中找不到对应的key，将其新添到链表中
        self.hash[t].append([key, value])  

    def get(self, key: int) -> int:
        t = key % 20011
        for item in self.hash[t]:
            if item[0] == key:
                return item[1]
        return -1  # 可能哈希的位置，所对应的链表不为空，但是不存在该值

    def remove(self, key: int) -> None:
        t = key % 20011
        for item in self.hash[t]:
            if item[0] == key:
                item[1] = -1

        除留余数法虽然不能完全避免哈希冲突，但它节省了大量在使用过程中不会用到的冗余空间，将未存入的元素对应的空间给其他可以使用这片空间的元素使用，使算法更有效率。

        同时，链表使得对 key 和 value 都能以数据形式存入数组，便于接下来可能的操作。

二、字符串

1. 验证回文串

描述：给定一个字符串 s。

要求：判断是否为回文串（只考虑字符串中的字母和数字字符，并且忽略字母的大小写）。

说明：

  • 1 <= s.length <= 2 * 105
  • s 仅由可打印的 ASCII 字符组成
class Solution:
    def isPalindrome(self, s: str) -> bool:

        # 初始化对撞指针
        i,j=0,len(s)-1

        while i<=j:
            # 获取有效元素
            while i<=j:
                # 转换字母大小写    
                if 65<=ord(s[i])<=90:
                    a = chr(ord(s[i])+32)
                    break
                # 取小写字母和数字
                elif 48<=ord(s[i])<=57 or 97<=ord(s[i])<=122:
                    a = s[i]
                    break
                # 跳过无效字符
                else:
                    i+=1

            while i<=j:    
                if 65<=ord(s[j])<=90:
                    b = chr(ord(s[j])+32)
                    break
                elif 48<=ord(s[j])<=57 or 97<=ord(s[j])<=122:
                    b = s[j]
                    break
                else:
                    j-=1

            # 移动指针
            try:
                if a==b:
                    i+=1
                    j-=1
                else:
                    return False

            # 回文串中只有一个有效元素，则只有a被赋值，导致错误
            except BaseException:
                return True

        # 全符合条件，是回文串
        return True

        使用对撞指针，只对字符串进行一次遍历。在遍历过程中，根据字串 ASCII 码值判定其是否为数字或字母，实现大小写转换，并跳过其它字符。

class Solution:
    def isPalindrome(self, s: str) -> bool:

        # 初始化对撞指针
        i,j=0,len(s)-1
        
        # 处理原字符串，使其符合规定格式
        while i <= j:    # while循环便于指针操作，不要用for循环
            if 65 <= ord(s[i]) <= 90:
                # str为不可变序列，选择replace函数进行定位修改或删除
                s = s.replace(s[i], chr(ord(s[i]) + 32))
                i += 1
            elif 48 <= ord(s[i]) <= 57 or 97 <= ord(s[i]) <= 122:
                i += 1
            else:
                s=s.replace(s[i], '', 1)
                j -= 1
        
        # 再次初始化指针
        i=0
        
        # 再次遍历，判定回文
        while i<=j:
            if s[i]==s[j]:
                i+=1
                j-=1
                continue
            else:
                return False
        
        return True

        增加了对字符串的操作量，遍历了两次字符串，在完成单个判定目标时效率较低，但如果有多个判定目标，后续操作会更方便。

class Solution:
    def isPalindrome(self, s: str) -> bool:

        l,r = 0,len(s)-1

        while l<r:

            while l<r and not s[l].isalnum():
                l += 1
            while l<r and not s[r].isalnum():
                r -= 1

            if l<r:
                if s[l].lower() != s[r].lower():
                    return False
                l += 1
                r -= 1

        return True

        这种解法与解法1思路相似，只是用 isalnum() 函数完成了数字/字母的判定，用 lower() 函数完成了大小写转换。

class Solution(object):
    def isPalindrome(self, s):

        # 正则留下非符号内容,再变为小写
        s=re.sub('[^a-zA-Z0-9]','',s).lower()

        # 回文串 = 回文串的倒序
        return s==s[::-1]

这种解法提供了全新的思路：

        首先使用了正则化函数 re.sub(pattern, repl, string, count=0, flags=0) 

  • pattern：模式字符串，表示被替换字符，“^” 表示取非，“a-z” 表示小写字母，“A-Z” 表示大写字母，“0-9” 表示数字
  • repl：要替换的字符串（可以是函数）
  • string：被处理（查找替换）的原字符串
  • count：替换的最大次数，默认替换所有
  • flags：编译时用的匹配模式（忽略大小写、多行模式等），数字形式，默认无

        其次，使用了新的回文判定，通过逆序切片得到倒序，利用回文串的性质判定。

2. 反转字符串

描述：给定一个字符数组 s。

要求：将其反转。

说明：

  • 不能使用额外的数组空间，必须原地修改输入数组、使用  O(1) 的额外空间解决问题。
  • 1 <= s.length <= 105
  • s[i] 都是 ASCII 码表中的可打印字符
class Solution:
    def reverseString(self, s: List[str]) -> None:
        i, j = 0, len(s)-1
        while i<j:
            s[i], s[j]= s[j], s[i]
            i += 1
            j -= 1

        对撞交换即可。

class Solution:
    def reverseString(self, s: List[str]) -> None:
        s.reverse()

        直接调用函数实现。

3. 反转字符串中的单词 III

描述：给定一个字符串 s。

要求：将字符串中每个单词的字符顺序进行反转，同时仍保留空格和单词的初始顺序。

说明：

  • 1 <= s.length <= 5 * 10e4
  • s 包含可打印的 ASCII 字符。
  • s 不包含任何开头或结尾空格。
  • s 里至少有一个词。
  • s 中的所有单词都用一个空格隔开。 
    class Solution:
    def reverseWords(self, s: str) -> str:

        # 初始化单词列表
        wl = []

        # 遍历字符串转成的单词列表
        for i in s.split(sep=' '):

            # 将单词转成列表
            l = [j for j in i]

            # reverse()：对列表进行翻转，无返回值
            l.reverse()

            # 连接单词，加入单词列表
            wl.append(''.join(l))

        # 空格连接单词。还原为字符串
        return ' '.join(wl)

        涉及了字符串与列表的转化和还原操作，但逆序是由内置函数完成的。

class Solution:
    def reverseWords(self, s: str) -> str:
        return ' '.join([w[::-1] for w in s.split()]) # split函数的sep参数默认值为空格

        但是字符串的逆序不必用列表的函数，可直接通过逆序切片进行反转，可节省一次数据结构转换。


4. 找出字符串中第一个匹配项的下标

描述：给定两个字符串 haystack 和 needle。

要求：在 haystack 字符串中找出 needle 字符串出现的第一个位置（从 0 开始）。如果不存在，则返回 -1。

说明：

  • 当 needle 为空字符串时，返回 0
  • 1 <= haystack.length, needle.length <= 10e4
  • haystack 和 needle 仅由小写英文字符组成
 理解KMP算法
# 生成 next 数组：next[j] 表示下标 j 之前的模式串 p 中，最长相等前后缀的长度
# 记模式串 p 被检查的前缀为检查区域，它的前缀为子前缀，此时的 left 所划定的子前缀为对应的已配区域
def generateNext(p: str):

    # 计算模式串长度
    m = len(p)
    # 初始化 next 数组：模式串 p 的前缀中，无相等前后缀
    next = [0 for _ in range(m)]
    # 初始化检查区域起始指针，即子前缀指针
    left = 0
    
    # 移动检查区域终止指针，调节其长度为 right+1                              
    for right in range(1, m):

        # 两端失配，left 进行回退，直到匹配成功，或者已退至检查区域起点
        while left > 0 and p[left] != p[right]:

            # next[left - 1]：上一个检查区域中，最长相等前后缀的长度
            # 退至上一个已配区域的右侧
            left = next[left - 1]

        # 匹配成功，找到相同前后缀，扩大已配区域
        if p[left] == p[right]:
            left += 1

        # 标记该长度的母前缀中，最长相等前后缀的长度
        next[right] = left
        # 延长检查的母前缀长度，更换至未配区域
                    
    return next

        KMP算法的核心思路是：文本串 T 与模式串 p 失配时模式串 p 的指针的回退，不必从头开始。若模式串 p 的已配区域中，存在相同的前后缀，那么 p 的前缀就不必重新匹配一次，因为匹配结果和后缀相同，只需让指针从“后缀的右侧”退至“前缀的右侧”继续匹配即可。

        那么需要一个数组 next 记录 p 的各个匹配区域 “前缀的右侧”的位置，即该区域最长相等前后缀的长度。通常，这个匹配区域是 p 的前缀，也就是我们的检查区域。我们仍可利用上述思想生成 next，即在生成时，用已知的 next 元素进行后续操作的回退。

        上述代码中，回退可能使 left 退至 0 ，以后的检查区域对应的 next 的元素都为 0 ，也可能回退过程中出现连续可配区域，使得 left 不断 +1，得到更长的相等前后缀的长度……

# KMP 匹配算法：T 为文本串，p 为模式串
def kmp(T: str, p: str) -> int:

    # 计算 T、p 的长度
    n, m = len(T), len(p)
    # 生成 next 数组
    next = generateNext(p)
    # 初始化 p 指针
    j = 0

    # 移动 T 指针
    for i in range(n):
        # 失配按 next 数组回退
        while j > 0 and T[i] != p[j]:
            j = next[j - 1]
        # 可配则移动 p 指针
        if T[i] == p[j]:
            j += 1
        # 模式串完全匹配成功，返回匹配开始位置
        if j == m:
            return i - j + 1

    # 匹配失败，返回 -1
    return -1

         Tp的匹配原理和 next 的生成原理实际同出一辙。

解法
class Solution:
    def strStr(self, haystack: str, needle: str) -> int:

        n, m, l, j = len(haystack), len(needle), 0, 0
        next = [0]*m    # 乘算比遍历更快一点 
    
        for r in range(1, m):
            while l > 0 and needle[l] != needle[r]:
                l = next[l - 1]
            if needle[l] == needle[r]:
                l += 1
            next[r] = l

        for i in range(n):
            while j > 0 and haystack[i] != needle[j]:
                j = next[j - 1]
            if haystack[i] == needle[j]:
                j += 1
            if j == m:
                return i - j + 1
        return -1

         KMP算法的解法。

class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        # 提前做简单判定在有些时候可以节省用时
        if needle not in haystack:
            return -1
        
        l = len(needle)
        for i in range(len(haystack)):
            if haystack[i:i+l] == needle:
                return i

        BF算法的解法。 

5. 重复的子字符串

描述：给定一个非空的字符串 s。

要求：检查该字符串 s 是否可以通过由它的一个子串重复多次构成。

说明：

  • 1 <= s.length <= 10e4
  • s 由小写英文字母组成
class Solution:
    def repeatedSubstringPattern(self, s: str) -> bool:

        # 字符串长
        n=len(s)

        # 单字母型
        if s==s[0]*n:
            if n==1:
                return False
            else:
                return True

        # 按长度的因数分割字符串：取1和长度本身以外的因数
        for i in range(2,n//2+1):
            if not(n%i):
                # 因数作为子串长
                for j in range(0,n,i): # j的上限充分大即可，尽量减少运算
                    # 分段匹配
                    if s[:i] != s[j + i:j + 2*i]:
                        break
                    if j + 2*i==n:
                        return True
        return False

​

        BF算法的变种，反正都很暴力。

class Solution:
    def repeatedSubstringPattern(self, s: str) -> bool:
        return s in (s+s)[1:-1]

​

        这种解法的思路是，将字符串与它自己拼接，然后 “掐头去尾” ，检查它是不是新主串的子串。

设字符串 s 由重复子串ss组成，充分性可以分成三种情况讨论：

  1. ss只有一个字母：显然符合以上条件；
  2. ss有两个或两个以上的字母，且在 s 中出现两次：记 ss = axb，其中 a，b分别是首尾字母， x 是任意字母序列或者空串，那么 s + s = axbaxb + axbaxb = a(xb[axb][axb]ax)b，符合以上条件；
  3. ss有两个或两个以上的字母，且在 s 中出现 n ( n > 2 ) 次：由上述知 s + s 掐头去尾后一定有 2n-2 > n个连续的 ss，即有子串 s = ss * n 。

必要性是显然的：

        若 s 有重复子串，且由连续重复子串段 AXB 和任意不同子串 cyd 组成， 那么只需讨论上述情况二，A(XB[cydAXB]cy)d，cyd 不等于 AXB，故新主串中不存在 s 。

        该解法的本质就是检查字符串 s 的前后缀是否相同，并且去除前后缀得到的字符串 s' 是否仍有相同性质。

6. 重复叠加字符串匹配

描述：给定两个字符串 a 和 b。

要求：寻找重复叠加字符串 a 的最小次数，使得字符串 b 成为叠加后的字符串 a 的子串，如果不存在则返回 -1。

说明：

  • 字符串 "abc" 重复叠加 0 次是 ""，重复叠加 1 次是 "abc"，重复叠加 2 次是 "abcabc"。
  • 1 <= a.length <= 10e4
  • 1 <= b.length <= 10e4
  • a 和 b 由小写英文字母组成
class Solution:
    def repeatedStringMatch(self, a: str, b: str) -> int:

        # KMP算法参数初始化
        res, n, m, l, j, k = 0, len(b), len(a), 0, 0, []
        next = [0]*m     
        
        # 包含：无需叠加
        if m>=n and b in a:
            return 1
        # 二次重叠
        if b in (a+a)[1:-1]:
            return 2
        
        # 多次重叠
        # KMP算法求 a 在 b 中出现的位置，将对应子串首元素下标储存在数组k中
        for r in range(1, m):
            while l > 0 and a[l] != a[r]:
                l = next[l - 1]
            if a[l] == a[r]:
                l += 1
            next[r] = l

        for i in range(n):
            while j > 0 and b[i] != a[j]:
                j = next[j - 1]
            if b[i] == a[j]:
                j += 1
            if j == m:
                k.append(i - j + 1) 
                j = 0

        # 完整的 a 出现次数
        nk = len(k)
        # b 中没有连续的 a
        if not(nk) or (nk > 1 and k[1]-k[0]!=m):
            return -1
        
        # 重叠次数 = 连续的完整或残缺的 a 出现次数
        res += nk

        # 左侧残缺
        if k[0]:
            # 残缺子串是否属于 a ：检测左侧一个元素
            if b[k[0]-1]==a[-1]:
                res += 1
            else:
                return -1
        # 右侧残缺
        if k[-1]+m<n:
            # 残缺子串是否属于 a ：检测右侧 a 长度单位的元素
            for i in range(min(m,n-k[-1]-m)):
                if b[k[-1]+m+i]!=a[i]:
                    return -1
            res += 1

        return res

         由上题知，重复叠加后得到的主串的子串，必然保持原主串的顺序，叠加次数与新主串中的原主串数量有着密切关系。以上是用KMP算法实现的。

class Solution:
    def repeatedStringMatch(self, a: str, b: str) -> int:

        # 最少叠加次 n ，最多叠加次 n+2
        n = len(b) // len(a)

        # 遍历检测
        for i in range(n, n+3):
            c = a * i
            # find函数判断 b 是否为 c 的子串
            if c.find(b) != -1:
                return i

        return -1

        由上个解法的叠加次数公式可以发现，不必精确计算 a 的出现位置，只需在一个小区间内试错检验，再用内置函数代替KMP实现子串存在判断即可。

7. 旋转字符串

描述：给定两个字符串 s 和 goal。

要求：如果 s 在若干次旋转之后，能变为 goal，则返回 True，否则返回 False。

说明：

  • s 的旋转操作：将 s 最左侧的字符移动到最右边
  • 1 <= s.length, goal.length <= 100
  • s 和 goal 由小写英文字母组成
class Solution:
    def rotateString(self, s: str, goal: str) -> bool:
        return goal in (s+s) and len(s)==len(goal)

​

        旋转后的字符串，也可以视作原主串二次叠加后，它的与原主串等长的子串。

class Solution:
    def rotateString(self, s: str, goal: str) -> bool:

        # 参数初始化
        n,m,flag=len(s),len(goal),1

        # 数组不等长
        if n!=m:
            return False

        # 数组等长
        for i in range(n):
            # 找可配点：若字符串有重复字母，则可能出现多个可配点
            # 需要全部检查，直到完全可配
            if s[i]==goal[0]:
                # 逆序匹配检查：对指针做减法防止索引过界，实现循环遍历
                for j in range(1,n):
                    if s[i-j]!=goal[-j]:
                        # 失配标记
                        flag=0
                        break
                # 未出现失配，完全可配
                if flag:
                    return True
                # 标记初始化
                flag=1

        return False

​

         不使用内置函数实现，利用了旋转字符串经循环遍历后次序不变的性质。

class Solution:
    def rotateString(self, s: str, goal: str) -> bool:
        cnt = 0
        while cnt < len(s):
            # 还原成功
            if s == goal:
                return True
            else:
                # 逆循环
                s = s[1:] + s[0]
            cnt += 1
        return False

        不去找可配点，而是对字符串继续旋转，直到整体匹配，利用了旋转字符串的周期性。

        值得一提的是，while 循环结构 + 指针 更容易处理索引过界问题，且用一个指针的内存空间继承了计算结果，省去了 if 判定的计算量。

8. 数组中的字符串匹配

描述：给定一个字符串数组 words，数组中的每个字符串都可以看作是一个单词。如果可以删除 words[j] 最左侧和最右侧的若干字符得到 word[i]，那么字符串 words[i] 就是 words[j] 的一个子字符串。

要求：按任意顺序返回 words 中是其他单词的子字符串的所有单词。

说明：

  • 1 <= words.length <= 100
  • 1 <= words[i].length <= 30
  • words[i] 仅包含小写英文字母。
  • 题目数据 保证 每个 words[i] 都是独一无二的。
class Solution:
    def stringMatching(self, words: List[str]) -> List[str]:
        # 初始化哈希表、单词数量、结果列表、词长界限
        hp, n, res, max, min  = [[] for _ in range(30)], len(words), [], 1, 29

        # 按词长将单词存入哈希表的对应下标，并计算哈希表的有效索引范围
        for i in range(n):
            index=len(words[i]) - 1
            hp[index].append(words[i])
            if max<index:
                max=index
            if min>index:
                min=index

        # 初始化二维指针
        i1, i2, j1, j2, f = min, 0, max, 0, f

        # 从短单词开始对所有比它长的单词进行判定 
        while min<=i1<max:           # 短词长指针范围            
            while i2<len(hp[i1]):    # 等长短词指针范围                
                while i1<j1<=max:    # 长词长指针范围                   
                    while j2<len(hp[j1]):               # 等长长词指针范围                        
                        if hp[i1][i2] in hp[j1][j2]:    # 短词是否为长词的子串                           
                            res.append(hp[i1][i2])      # 加入结果数组                           
                            f=1        # 判定结束标志
                            break
                        else:                            
                            j2+=1      # 移动等长长词指针                    
                    j2=0               # 初始化等长长词指针        
                    if f:
                        break                    
                    j1-=1    # 移动长词长指针            
                f=0          # 初始化标志
                j1=max       # 初始化长词长指针      
                i2+=1        # 移动等长短词指针            
            i1+=1            # 移动短词长指针            
            i2=0             # 初始化等长短词指针

        return res

        这题的关键是对词长进行排序后才能完成全排列判定，这里人工建立了一个哈希表完成排序。

class Solution:
    def stringMatching(self, words: List[str]) -> List[str]:

        # 在words列表内原地按词长排序
        words.sort(key= lambda x:len(x))

        # 参数初始化
        ans,l = [],len(words)

        # 从短到长检查
        for i in range(l-1):
            for j in range(i+1,l):
                if words[i] in words[j]:
                    ans.append(words[i])
                    break
        return ans

        这个解法则是使用了 sort 函数进行原地排序，本质上也是哈希表的应用。

class Solution:
    def stringMatching(self, words: List[str]) -> List[str]:
        a = " ".join(words) # 注意，连接符是空格，使得不同单词的连接处不会产生新的重复子串
        return [w for w in words if a.count(w)>1]

         这种解法的妙处在于，将子串判定转化为了连缀字符串是否存在连续子串的问题。

9. 查找给定哈希值的子串

描述：如果给定整数 p 和 m，一个长度为 k 且下标从 0 开始的字符串 s 的哈希值按照如下函数计算：

hash(s, p, m) = (val(s[0]) * p0 + val(s[1]) * p1 + ... + val(s[k-1]) * pk-1) mod m

其中 val(s[i]) 表示 s[i] 在字母表中的下标，从 val('a') = 1 到 val('z') = 26。

现在给定一个字符串 s 和整数 power，modulo，k 和 hashValue 。

要求：返回 s 中 第一个 长度为 k 的 子串 sub，满足 hash(sub, power, modulo) == hashValue。

说明：

  • 子串：定义为一个字符串中连续非空字符组成的序列。
  • 1 <= k <= s.length <= 2 * 10e4
  • 1 <= power, modulo <= 10e9
  • 0 <= hashValue < modulo
  • s 只包含小写英文字母。
  • 测试数据保证一定 存在 满足条件的子串。

'''RK算法：将子串元素的ASCII码依次排列得到 x 进制数，索引决定位数，
然后转化为 y 进制作为该子串的哈希值，与模式串的哈希值匹配'''

# 本题中，s 为主串，power 为目标进制，modulo 为取模的值，k 为模式串的长度，
# hashValue 为模式串的哈希值，特别的，模式串是 s 的子串。
# 与传统RK算法不同的是，本题的哈希公式的目标进制与字符种类不相同，
# 元素的码值为字母表序数，取模的值也较小，并且索引越大位数越高。
class Solution:
    def subStrHash(self, s: str, power: int, modulo: int, k: int, hashValue: int) -> str:

        # 初始化参数：子串哈希值，主串长，最高位幂
        hs, n, p = 0, len(s), pow(power, k-1)

        # 计算第一个模式串的哈希值：逆序遍历转换进制
        for i in range(k-1,-1,-1):
            hs = hs * power + (ord(s[i])-96)    # ASCII码-96即为小写字母序数

        # 顺序检查每一个子串：指针为当前子串第一个元素的索引
        for i in range(n - k + 1):

            # 匹配成功，返回子串
            if hs % modulo == hashValue:
                return s[i:i+k]
           
            # 失配
            if i < n - k: 
                # 移除最低位
                hs -= ord(s[i])-96
                # 全部降位，加入最高位
                hs = hs // power + (ord(s[i+k])-96)*p

        由于不知道模式串内容，无法检验哈希冲突，并且移位时使用了整除运算，所以不能随意对哈希值取模，牺牲稳定性以减少计算量。

class Solution:
    def subStrHash(self, s: str, power: int, modulo: int, k: int, hashValue: int) -> str:

        # 初始化参数：主串长，码值字典，哈希格，位幂格
        n, mp, f, g, h = len(s), {chr(96+i):i for i in range(1,27)}, [0]*(k+1), [0]*(k+1), [1]*(k+1)
        '''
        码值字典：通过字典生成式，得到所有字母对应的码值，方便快速调用
        哈希格：f[0]为当前字串的哈希值，其余格为迭代转换进制的过程结果，留一格防索引过界
        邻哈希格：g[k]为下一子串的哈希值，为防重复计算下一个f[0]，代码没有计算g[k]
        位幂格：保存每一位转换时应乘的 进制^位数-1 的幂，同样预留一格'''

        # 对进制取模：缩小哈希值
        power %= modulo

        # 生成位幂格：省略重复的幂运算
        for i in range(1,k+1): h[i] = h[i-1] * power % modulo

        # 按 k 等分检查子串：指针为当前子串第一个元素的索引 
        for i in range(0,n,k):

            # 生成哈希格：逆向遍历，保留运算过程，供移位运算使用
            for j in range(k-1,-1,-1): 
                f[j]=(f[j+1]*power+mp[s[i+j]])%modulo

            # 匹配成功，返回子串
            if(f[0] == hashValue): return s[i:i+k]

            # 生成邻哈希格：正向遍历，取当前子串右侧不超过 k 个元素
            # 子串右侧剩余元素量 n-i-k：防止索引过界
            # 下一个子串对应位置的索引 i+k+j-1
            for j in range(1,min(k,n-i-k+1)): g[j]=(g[j-1]+mp[s[i+k+j-1]]*h[j-1])%modulo

            # 两个哈希格对应索引处的哈希值经以下运算可以生成两个 k 段间其余子串的哈希值
            for j in range(1,min(k,n-i-k+1)):
                if((f[j]+g[j]*h[k-j])%modulo == hashValue): 
                    return s[(i+j):(i+j+k)]


'''此算法大大节省了遍历次数，使得时间复杂度O(n)降为了O(n/k)，运行实例如下：
s = 'abcdef'; k = 3

f [3*p^2 + 2*p + 1] [3*p + 2] [3] [0]
g [0] [4] [4*p + 5] [0]([4*p^2 + 5*p + 6])
h [1] [p] [p^2] [p^3]

hash['abc'] = f[0]
hash['bcd'] = f[1]+g[1]*h[3-1]
hash['cde'] = f[2]+g[2]*h[3-2]
hash['def'] = g[k] = f'[0]'''

        优化了整除运算后，取模限制被解除，牺牲了少量空间换取了大量时间。 

dandellion_
关注
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值