《漫画傅里叶解析》作者 涉谷道雄
第7章 傅里叶解析
一、 研究频率成分的步骤
傅里叶解析是求解原波形(函数)由哪些频率的波以怎样的大小组合而成的方法。
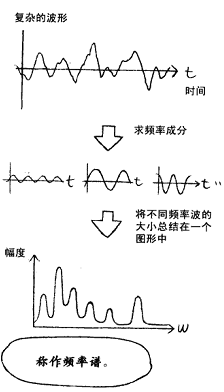
- 步骤1:首先,为了将复杂波形转为周期函数,从波形中取出一段区间。将这个区间看做最大的周期,对应的频率为1Hz,为最小的频率。
取出1秒长度的区间中含有振动1000次的成分是频率为1kHz的频率成分。 - 步骤2:从最低频率开始,到可能出现的最高频率,需要对所有频率一一进行分析。
- 步骤3:从切取的波形中分析出某种特定的频率成分,需要使用滤波器,将成分一个一个的分解出来。
- 步骤4:测量分解出来的频率成分的量,然后依次排开,就得到了频率谱。
二、 傅里叶系数
F
(
x
)
=
1
2
a
0
+
a
1
c
o
s
x
+
a
2
c
o
s
2
x
+
a
3
c
o
s
3
x
+
.
.
.
+
a
n
c
o
s
n
x
+
.
.
.
F(x)=\frac{1}{2}a_0+a_1cosx+a_2cos2x+a_3cos3x+...+a_ncosnx+...
F(x)=21a0+a1cosx+a2cos2x+a3cos3x+...+ancosnx+...
+
b
1
s
i
n
x
+
b
2
s
i
n
2
x
+
b
3
s
i
n
3
x
+
.
.
.
+
b
n
s
i
n
n
x
+
.
.
.
+b_1sinx+b_2sin2x+b_3sin3x+...+b_nsinnx+...
+b1sinx+b2sin2x+b3sin3x+...+bnsinnx+...
=
1
2
a
0
+
∑
n
=
1
∞
(
a
n
c
o
s
n
x
+
b
n
s
i
n
n
x
)
=\frac{1}{2}a_0+\sum^{\infty}_{n=1}(a_ncosnx+b_nsinnx)
=21a0+n=1∑∞(ancosnx+bnsinnx)
如果F(x)是随时间变化的函数,用F(t)表示。
这里
a
0
a_0
a0,
a
n
a_n
an,
b
n
b_n
bn 叫做傅里叶系数,
步骤3就是求傅里叶系数。
- a 0 a_0 a0决定波形的全体值在y轴上的上下位置的值。
- 从各种频率成分中,抽取某一特定频率成分,必须想到的是“函数的正交”,由于函数正交的关系,它们乘积的定积分的结果为0,而sinnx和cosnx都与自身不成正交关系,都有一定的值。因此,正交关系的性质,使频率成分的分解成为可能。
- 首先看cos的傅里叶系数
a
n
a_n
an,如果想要结果只剩下
a
n
c
o
s
n
x
a_ncosnx
ancosnx,那么将F(x)全体乘以cosnx,然后做定积分。因为其它正交积分为0,所以只剩下一个cosnx的值。这样
a
n
a_n
an的值就求出来了。
∫ 0 2 π s i n n x s i n n x d x = ∫ 0 2 π 1 2 ( 1 − c o s 2 n x ) d x \int_0^{2\pi} sinnxsinnxdx=\int_0^{2\pi}\frac{1}{2}(1-cos2nx)dx ∫02πsinnxsinnxdx=∫02π21(1−cos2nx)dx
= 1 2 ∫ 0 2 π 1 d x − 1 2 ∫ 0 2 π c o s 2 n x d x = 1 2 [ x − 1 2 n s i n 2 n x ] 0 2 π = π =\frac{1}{2}\int_0^{2\pi}1dx-\frac{1}{2}\int_0^{2\pi}cos2nxdx=\frac{1}{2}[x-\frac{1}{2n}sin2nx]^{2\pi}_0={\pi} =21∫02π1dx−21∫02πcos2nxdx=21[x−2n1sin2nx]02π=π
同样, c o s 2 n x cos^2nx cos2nx的积分结果也为 π {\pi} π
整理得到傅里叶系数的三个表达式:
a n = 1 π ∫ 0 2 π F ( x ) c o s n x d x a_n=\frac{1}{\pi}\int_0^{2\pi}F(x)cosnxdx an=π1∫02πF(x)cosnxdx
b n = 1 π ∫ 0 2 π F ( x ) s i n n x d x b_n=\frac{1}{\pi}\int_0^{2\pi}F(x)sinnxdx bn=π1∫02πF(x)sinnxdx
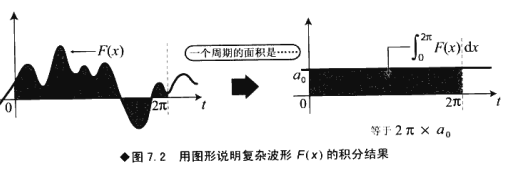
a 0 = 1 2 π ∫ 0 2 π F ( x ) d x a_0=\frac{1}{2\pi}\int_0^{2\pi}F(x)dx a0=2π1∫02πF(x)dx
第四步:在研究频率谱时,傅里叶系数并不完全等于不同成分的大小,因此需要求解频率成分的大小。求r
r
n
=
a
n
2
+
b
n
2
r_n=\sqrt{a^2_n+b^2_n}
rn=an2+bn2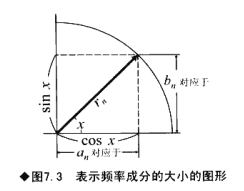
第五步,将第四步求的r 从小到大排列画在图形中就得到了频率谱。
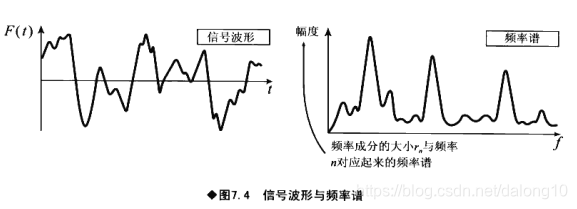
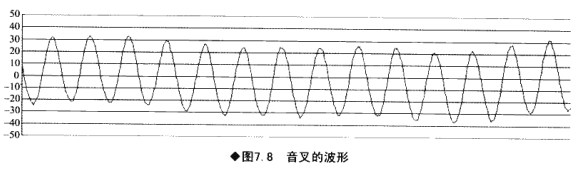
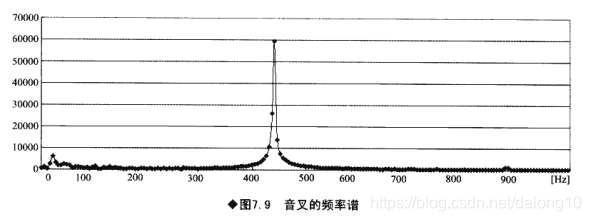
三、 音叉的频率谱
轻轻敲音叉,能感觉“拉”音的基本频率400Hz的振动。拉=440Hz
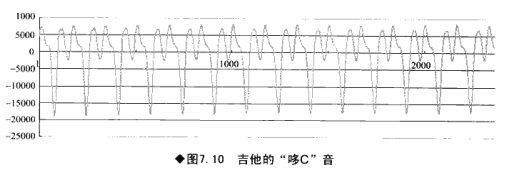
四、 吉他的频率谱
吉他单音“哆C”的分析,波形和频谱
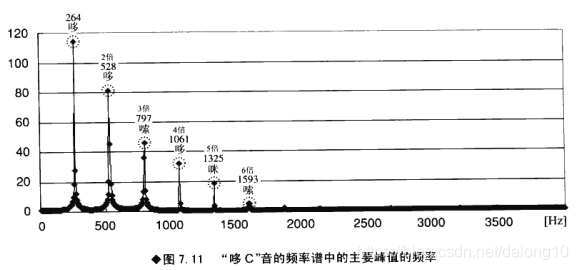
“拉”音的440Hz频率是国际标准频率,国际标准的“哆”音频率是261.63Hz。解析结果中最大的频率在264Hz处,很接近。528Hz、797Hz、1061Hz、1325Hz、1593Hz…是“哆”音频率的2倍、3倍、4倍…这些频率的幅度大小随着频率的增大而渐渐变小,可以说,基准音“哆”的高音调波中既含有偶数倍基准频率也含有奇数倍基准频率。
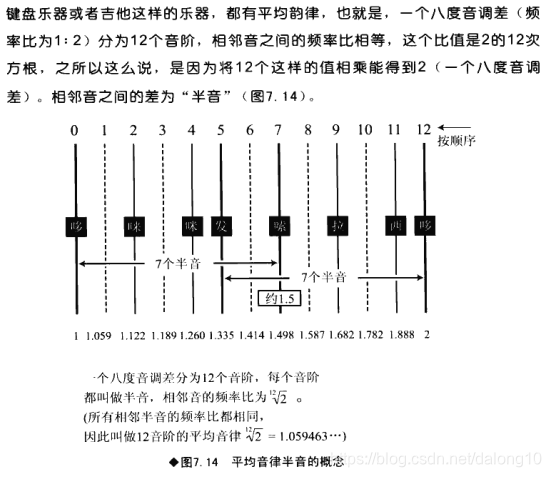
“哆”和“嗦”的频率比=2:3 ;“哆”和“咪”的频率比=6:7 ;“咪”和“嗦”的频率比=7:9 。频率比值越简单,音能之间越能彼此加强。重要的频率成分没有改变,所以和音的音色比较浓厚。
五、 人的声音频率谱
通过声带振动形成的含有许多频率成分的空气的振动,通过口腔或鼻腔的时候,根据它们的形状会组合成具有许多特征的频率成分,即口腔和鼻腔相当于滤波器,这样人就能发出各种各样的声音了。
六、 柔和的声音
音域是发出最低音到最高音的音程。音域广是好嗓子的重要基础。接着是,频率谱中有比较简单的各种频率成分的共鸣关系。
共鸣关系是指低音,即以某个频率为基准,完好的含有这个频率的整数倍的频率的波的状态。





 本文深入探讨傅里叶解析的基础原理,包括频率成分分析步骤、傅里叶系数的计算方法,以及在音叉、吉他和人声等实际场景中的应用,揭示了频率谱的奥秘。
本文深入探讨傅里叶解析的基础原理,包括频率成分分析步骤、傅里叶系数的计算方法,以及在音叉、吉他和人声等实际场景中的应用,揭示了频率谱的奥秘。
















 8551
8551

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








