广度优先:采用队列结构先进先出,无回溯操作(即无入栈、出栈操作),保留全部结点,所占空间较大,运行速度快,空间换时间
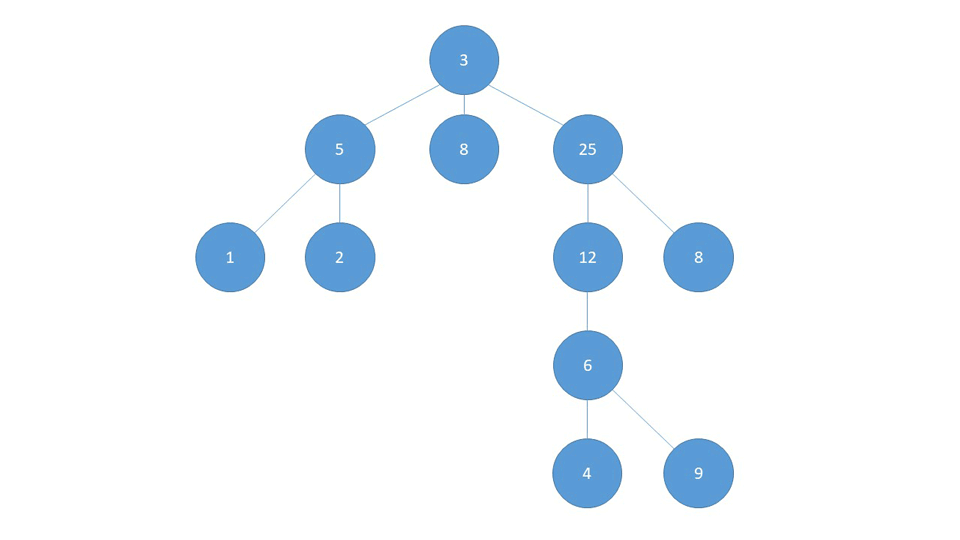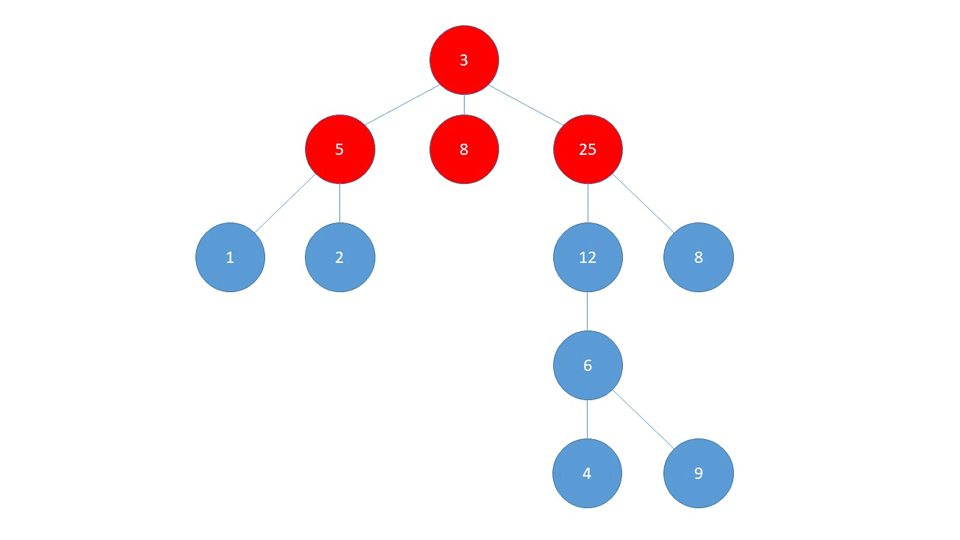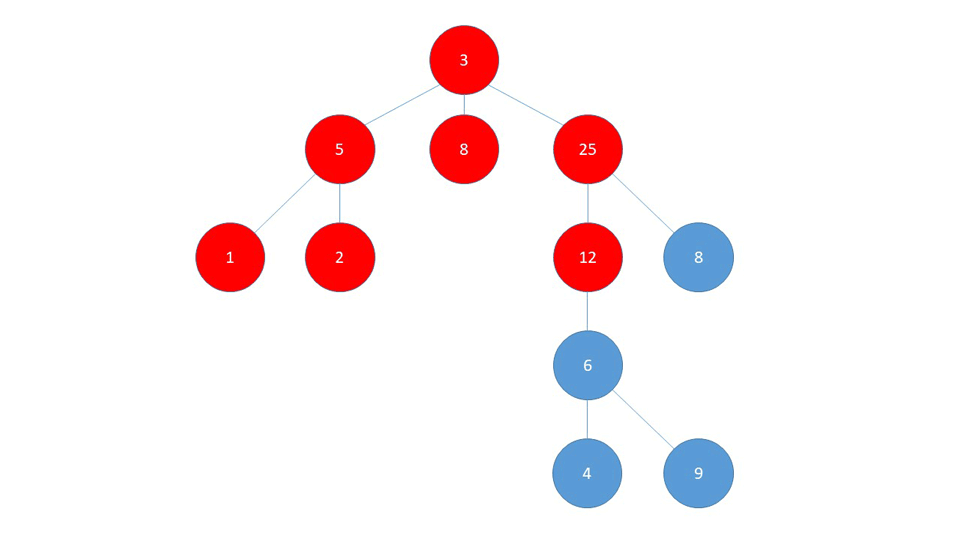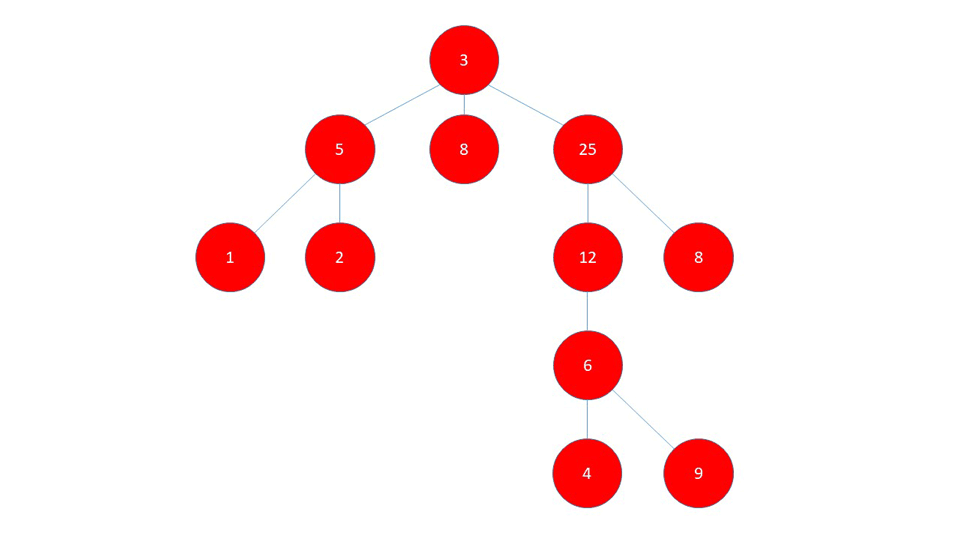
数据格式
header:表头是一个树结构
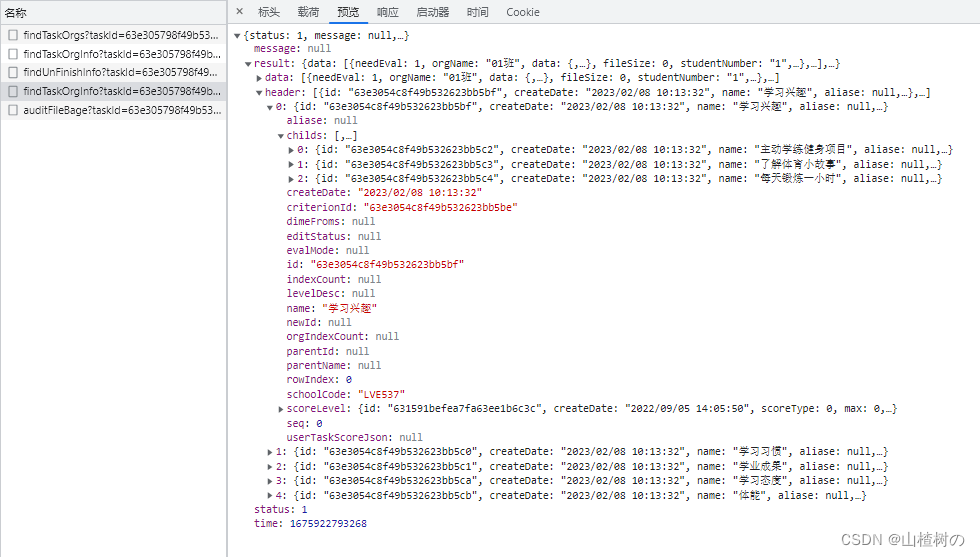
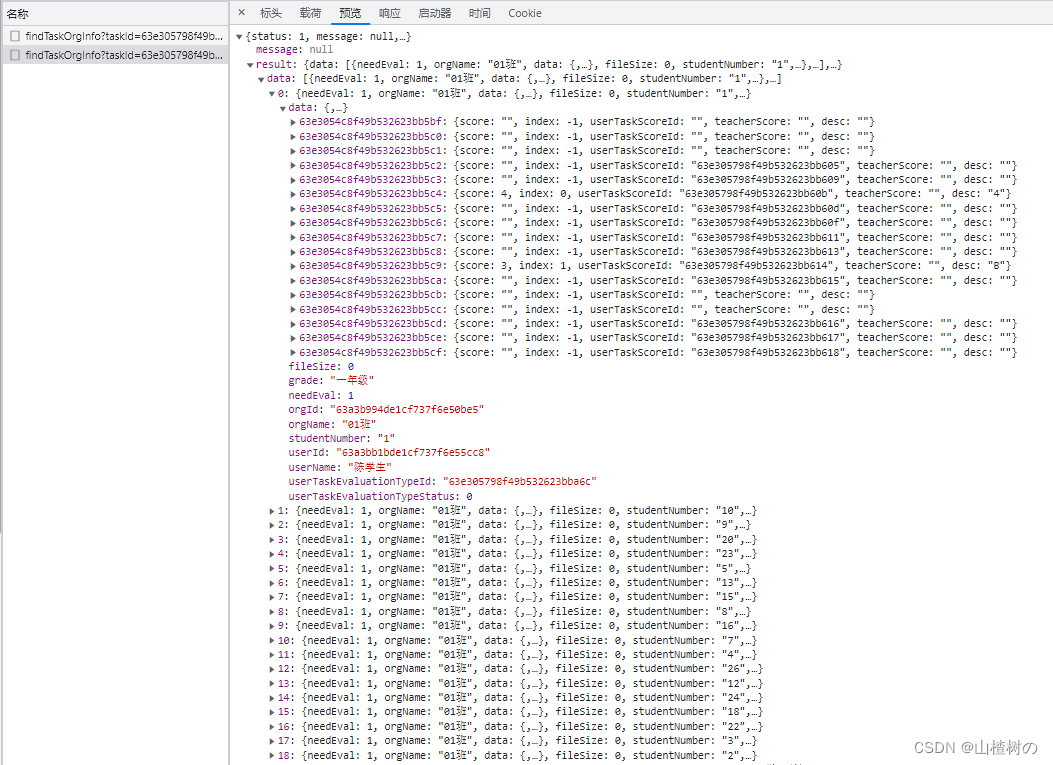
data:表主体是一个数组,数组里每一项都会对应一个map集,map集的id又对应着表头树结构每个节点最子级项,
逻辑部分:
大致思路:既然提到多级表头,合并行合并列肯定少不了,先把树结构处理为一层数据结构,开始计算合并行,每个节点需要合并的行数需要判断一下 当前节点的层级是否不等于整个树结构的最大层级并且当前节点下是否有子节点,如果满足上述条件,则需要合并行,合并的数量为:最大层级数 - 当前节点层级 + 1;然后是合并列,每个节点合并的列数为:无子级节点1,、有子级节点:当前节点下所有子级数量的和;在给每个节点做好需要合并的行列数的标识后,可以开始处理用来循环表头的数据。处理一个二维数组,每项的数组中分别存放的是层级相同的节点,[[1,2], [1-1, 1-2, 2-1, 2-2], [1-1-1, ...], ...]
let arr = [
[]
] //处理后的数据
let newArr = []
table.compuedRowspan(nodes) // nodes是接口返回的树结构(处理前的表头数据)
table.compuedColspan(nodes)
table.treeToArr(nodes, arr)
table.getLastList(nodes, newArr)
table.headerList = arr // 处理后的表头
table.lastList = newArr // 用于渲染td的数据(树结构所有最子级节点)
const table = reactive({
map: {},
maxlevel: 0,
headerList: [],
lastList: [],
// 计算合并行
compuedRowspan(nodes) {
let maxlevel = 0; // 最大深度
let arr = [];
let map = {}
for (let i = 0; i < nodes.length; i++) {
nodes[i].level = 1; // 设根节点深度1
arr.push(nodes[i]);
maxlevel = 1;
}
// 给各个节点打标识 level
for (let n = 0; n < arr.length; n++) { // 先循环所有根节点,当前根节点下有子节点,则往数组push,所有根节点循环完毕后,开始循环刚刚push的子节点,当前子节点下还有子节点,则依次类推,继续push追加,然后循环遍历,直至循环到最后一个无child的子节点为止
if (arr[n].childs && arr[n].childs.length > 0) {
for (let t = 0; t < arr[n].childs.length; t++) {
arr[n].childs[t].level = arr[n].level + 1; // 让当前子节点的深度为父级的深度+1
if (maxlevel < arr[n].childs[t].level) { // 如果当前子节点的深度 > 默认深度1,给最大深度赋值
maxlevel = arr[n].childs[t].level;
}
arr.push(arr[n].childs[t]); // 开始push当前节点的子级
}
}
// map : 通过id拿到当前节点
map[arr[n].id] = arr[n]
}
table.map = map
table.maxlevel = maxlevel;
// 计算各个节点需要合并行数
for (let num = 0; num < arr.length; num++) { // 循环广度优先处理后的数据 [1, 2, 3, 1-1, 1-2, 2-1, .....]
if (arr[num].level !== maxlevel && (!arr[num].childs || arr[num].childs.length === 0)) { // 节点深度不等于最大深度并且当前节点下没有子级,说明当前节点需要合并行
arr[num].rowspan = 1 + maxlevel - arr[num].level;
} else {
arr[num].rowspan = 1;
}
}
},
// 计算合并列
compuedColspan(nodes) {
var colspan = 0;
for (let n = 0; n < nodes.length; n++) {
if (nodes[n].childs && nodes[n].childs.length > 0) { // 节点下有子节点,那么合并列数为下面子节点个数和,没有子节点为1
nodes[n].colspan = table.compuedColspan(nodes[n].childs);
} else {
nodes[n].colspan = 1;
}
colspan += nodes[n].colspan;
nodes[n].index = n
}
return colspan;
},
// 处理数据 生成用于循环表头的数据 [[1, 2], [1-1, 1-2, 2-1], [1-3, 2-3], ...]
treeToArr(nodes, newArr) {
let arr = []
table.lastList = []
for (let num = 0; num < nodes.length; num++) {
arr.push(nodes[num])
}
for (let chir = 0; chir < arr.length; chir++) { // 最开始循环根层数据,所有跟层循环后,依次子级
if (!newArr[arr[chir].level - 1]) { // 借用当前节点深度判断 表头数据newArr [[]],是否为真,不为真也就说明开始循环第二层节点数据(level = 2),依次类推
newArr[arr[chir].level - 1] = [] // 用于存放第二/第三/...层级的所有节点
}
newArr[arr[chir].level - 1].push(arr[chir]) // [[一级], [二级], [三级]]
if (arr[chir].childs) {
for (let item = 0; item < arr[chir].childs.length; item++) {
arr.push(arr[chir].childs[item])
}
} else {
table.lastList.push(arr[chir]) // 渲染td数据,所有最子级数据,按照顺序依次push
}
}
// console.log(arr, '广度优先结果 1-2-11-22-111-222');
},
// 计算用于循环td的数据(所有节点最子级)
getLastList(nodes, newArr) {
for (let i = 0; i < nodes.length; i++) {
if (!nodes[i].childs || nodes[i].childs.length == 0) {
newArr.push(nodes[i])
} else {
table.getLastList(nodes[i].childs, newArr);
}
}
}
})
渲染部分:
<table ref="tableRef" id="table__confirm">
<thead ref="tableTheadRef" id="tableTheadRef">
<tr v-for="(item, index) in table.headerList" id="tableOneTr">
<th class="number noBorder newindex" v-if="index === 0" :rowspan="table.maxlevel" id="firstTh">
<span v-if="propsParams.groupType !== 0">年级/班级/</span><span>学号</span>
</th>
<th class="number newindex" v-if="index === 0" id="secondTh" :rowspan="table.maxlevel">姓名</th>
<th class="newindex" v-for="(chir, chirindex) in item" :colspan="chir.colspan"
:rowspan="chir.rowspan">
{{ chir.name }}
</th>
</tr>
</thead>
<tbody>
<tr class="table-count" v-for="(item, index) in newTableData" @click="toRouter(item)">
<td :style="tableRowClassName(item)" :width="computedWeight">
<span v-if="propsParams.groupType !== 0">{{ item.grade }} {{ item.orgName }}</span>
{{ item.studentNumber }}号
</td>
<td :style="tableRowClassName(item)" style="position: relative; " :width="computedWeight">
{{ item.userName }}
</td>
<td class="model_pos" :style="tableRowClassName(item)" :width="computedWeight"
v-for="(arr, arrIndex) in table.lastList">
xxxxxxxxxxxxxxxxxx
</td>
</tr>
</tbody>
</table>
效果:
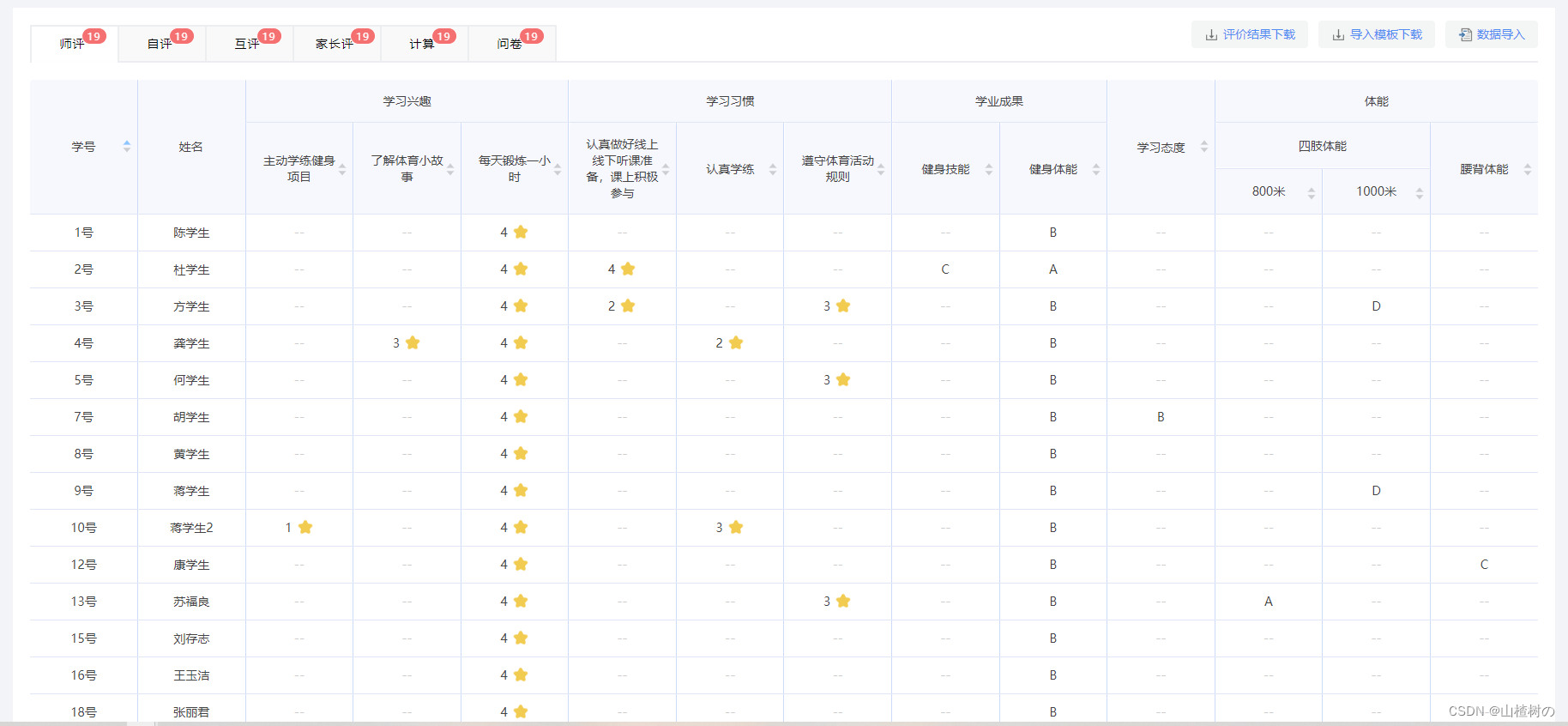







 文章讲述了如何利用广度优先搜索策略处理树结构数据,以实现多级表头的合并行和合并列功能。首先将树结构转换为一层数据结构,然后计算每个节点的行合并数和列合并数,最后进行表头和表格数据的渲染。这种方法通过牺牲空间来换取更快的运行速度。
文章讲述了如何利用广度优先搜索策略处理树结构数据,以实现多级表头的合并行和合并列功能。首先将树结构转换为一层数据结构,然后计算每个节点的行合并数和列合并数,最后进行表头和表格数据的渲染。这种方法通过牺牲空间来换取更快的运行速度。

















 3234
3234












