基于手臂刚度的外骨骼阻抗控制

原创于 2025-10-01 05:26:16 发布 · 836 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#外骨骼 #阻抗控制 #手臂刚度 #肌电图 #肘关节

部署运行你感兴趣的模型镜像

基于操作员手臂刚度的工业外骨骼调制阻抗肘部肌肉骨骼模型

1. 外骨骼定义

人类具有运动的自然控制能力，但施加的力受限于肌肉力量。相比之下，机器人操纵器可以执行需要高力输出的任务，但控制算法无法提供人类自然实现的灵活性和操作质量。外骨骼通过结合人类与机器人的技能，可能代表一种有趣的解决方案[1]。

外骨骼的定义仍存在争议[2]。尽管存在差异，但所有研究确定的主要特性是：外骨骼是一种涉及直接人机交互的可穿戴设备。这种交互既包括从机器人到人的作用，也包括从人到机器人的作用。前者源于外骨骼的内在特性，表现为认知层面（外骨骼向操作员提供反馈）和生物力学方面（外骨骼在自身结构上施加可控力）[3]。

后者可通过不同方式实现，这些方式定义了外骨骼代际。目前识别出三代外骨骼[2]：用户通过（1）自身的运动学、（2）动态方式、以及（3）通过记录的神经肌肉信号来控制外骨骼，肌电图 (EMG)。

第一代外骨骼用于辅助人体运动并施加一组预设关节角度轨迹。基于位置控制的外骨骼示例是为军事目的开发的哈迪曼[4]，可增强性能。在第二代外骨骼中，通常应用两种控制策略[5]。第一种涉及开环控制，即根据位置（如下肢外骨骼步态周期的阶段）施加预设力或扭矩值。第二种策略包括与用户和外骨骼之间交换的力/扭矩成比例的控制。示例包括用于负重的BLEEX[6]以及用于康复的ALEX[7]和 ARMin[8]。

第三代外骨骼最初是为上肢开发的[2]。使用肌电信号驱动外骨骼可使用户感受到更自然的运动，因为无需对外骨骼施加动作。事实上，肌电信号在肌肉发生机械收缩前约20–80毫秒就会出现[9]，从而可以在运动之前对信号进行评估。基于肌电图的外骨骼已针对上肢和下肢开发。

外骨骼还可以根据其使用领域进行分类。最早的外骨骼原型是为军事用途开发的[4]。另一个常见的应用是在康复领域。在此，外骨骼可以增强虚弱患者（如老年人或患有疾病而无法施加足够力量的患者）所施加的力，或者在康复训练期间辅助理疗师[10]。外骨骼还被提议作为农业工人的支撑装置或用于背部支撑。最近，用于工业用途的外骨骼 [11, 12]正在被考虑。预计在外骨骼学和减轻疲劳方面将产生有益效果，特别是在不适姿势下工作时[13]。

在制造过程中，某些操作可能由于不稳定的特性或要求高精度而需要关节僵硬。在这些操作中，施加的力的放大可能并非必要。然而，开发一种外骨骼（其目的是增加关节刚度而不增加施加的末端力）在执行不同操作时可能产生有益效果。

示意图0

2. 外骨骼与手臂阻抗

在工作过程中，操作员会与环境及大量工具进行交互。当交互不稳定时，需要调节肢体阻抗。肢体阻抗通过肌肉共激活实现。不同研究者分析了手臂阻抗（惯性、阻尼和刚度）在动态[14, 15] 和等长任务[16–18]中的表现。末端刚度定义为手部受到的外部施加位移与相应产生的力之间的关系[19, 20]。

末端刚度具有各向异性[21, 22]，并可用椭圆图形表示[23]。调节刚度的肌肉模式在动态[24, 25]和等长任务[26, 27]中均有研究。

许多外骨骼采用不同类型的阻抗控制进行开发，这是一种调节传统刚性高惯性机器人操纵器以及冲击管理系统中产生的高机械阻抗的方法[28]。一些康复外骨骼应用阻抗控制来驱动患者的肢体[29, 30]或减轻手部震颤[3]。然而，在所有这些情况下，阻抗并非根据用户的肢体阻抗计算得出。

在文献中，通过肌电信号控制的机器人装置被开发用于更安全的人机接口，或在外部力未知的情况下进行机器人操作。基于所用肌电信号的机器人装置阻抗控制已由不同研究团队开发[31–33]。此外，还开发了基于肌电信号的实时阻抗控制，用于调节上肢假肢的刚度[34]。在HAL外骨骼[35]中，下肢根据步态的不同阶段呈现不同的阻抗。然而，目前尚未开发出通过操作员记录的生物信号直接控制刚度的外骨骼用于工业应用。

3. 任务定义

如前所述，刚度调节在不同类型的作业中非常有用。根据任务的特性，可将需要刚度调节的作业进行分类。可分为两类已识别。

等长操作 ：需要施加力，但不要求运动。
动态操作 ：要求运动，但不需要施加较大力。

这种分类不仅源于对任务的动态描述，而且似乎也内在于中枢神经系统（CNS）之中。事实上，尽管在动态任务期间，刚度椭圆会与不稳定性方向对齐（如在接球任务[36]和指向任务[37]中所观察到的），但在等长任务期间仅观察到较小的旋转[17, 38]。另一种关于手臂刚度所需操作的分类则取决于操作员使其手臂变僵硬的原因。已确定了两个原因：

外部不稳定性 ：受试者对可能引起不稳定的位移具有感觉运动反馈。这种不稳定性可能由多种原因导致：设备本身（例如，设备发动机的旋转部件）、设备与其它物体的相互作用（例如，由于钻孔动作引起的振动）、设备使用环境（例如，多风环境）、操作员的工作条件（例如，移动平台）或操作员的生理性震颤（例如，疲劳）。
预测性不稳定性 ：操作员凭借经验知道可能会发生某些不稳定性，因此会通过绷紧关节来防止不稳定性。当加工材料不均匀时（例如木材上的肋条），可能出现这种行为。操作员所处的环境或使用的工具可能产生非预期的作用（例如钻床可能导致被钻物体脱离操作员的手）。某些操作可能导致不稳定配置（例如使用螺丝刀施加与平面非正交的力）。出于安全原因也可能出现此类行为（例如处理危险物质或设备，其错误使用可能导致伤害）。

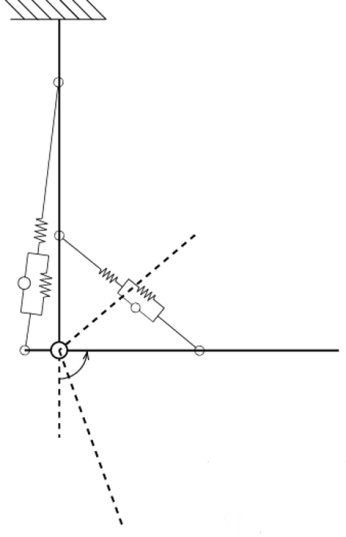
手臂所需的刚度增强可以沿不同方向进行：它可以与力的方向或运动方向相同，也可以相对于它们呈现不同的角度。运动学任务类型与僵硬原因的结合，导致了外骨骼应执行的不同任务的确定。针对每组情况，均确定了典型加工方法以及不稳定性方向与力的方向之间的角度（图1）：

等长任务，外部不稳定性 ：使用钻头与平面接触时的情况。虽然没有运动，但需要施加力。工人感受到的不稳定性是钻头与平面相互作用以及钻头电机旋转共同导致的结果。需要进行刚度调节以减少振动。肢体需要在所有与钻孔方向正交的方向上增加刚度。无需在其他方向上沿垂直于平面的方向（即力的作用方向）所需。
动态任务，外部不稳定性 ：使用电动工具在平面上雕刻。需要运动，但不需要施加力。工人感受到的不稳定性是由设备电机旋转引起的。需要刚度以减少振动。所有与雕刻方向正交的方向都是需要加强刚度的轴。沿雕刻方向无需加强刚度。
等长任务，预测性不稳定性 ：使用螺丝刀（当螺丝仍在平面外时）。此时没有运动，但需要施加力以开始旋入螺丝。不稳定性源于螺丝与平面之间的耦合（例如，若施加的力方向未精确正交于平面，将导致不稳定性）。操作员绷紧手臂以防止可能出现的任何不稳定性。在钻孔方向的正交方向上需要增加刚度，但在平行于力的方向上不需要刚度。
动态任务，预测性不稳定性 ：手工雕刻平面。需要进行运动，但由于所需的精度，工人必须精确调节施加的力。不稳定性源于待雕刻平面材料的非均质性，并由工人预先判断。操作员通过增强肢体在垂直于雕刻方向的所有方向上的刚度来减小由非均质性引起的不稳定性。在雕刻方向上无需增强刚度。

如可在每次操作中观察到的，如果沿特定方向施加运动或力，则需要通过增加手臂刚度来补偿的不稳定性通常出现在一个正交方向上。沿运动方向或力的施加方向增加刚度可能是有害的，因为它会阻碍运动或减小施加的力。

因此，系统需要选择需要增加刚度的方向，并降低在其他方向上的刚度。出于这个原因，必须尽可能精确地了解操作员希望施加的手臂刚度。

4. 外骨骼概念

示意图1

图2展示了一个上肢外骨骼在通过实时记录操作员肌肉激活来控制其阻抗情况下的人机交互框图。

人类操作员的中枢神经系统激活肌肉，以产生手臂的力和刚度。肌肉模式的选择由中枢神经系统计算，并基于反馈和前馈控制。关于人类中枢神经系统中生物控制机制的认知仍存在争议。

操作员施加的力和刚度是基于其肌肉激活水平以及手臂的配置（“数据处理”模块）计算得出的。

一旦确定了操作员所需的力和刚度，就需要计算外骨骼电机的激活水平（“控制”模块）。该操作可分为两个步骤：首先计算外骨骼需要施加的力和刚度，以降低用户的肌肉激活水平（“控制律”模块），然后计算电机的激活水平。这一过程通过外骨骼模型（“外骨骼模型”模块）来实现。外骨骼施加的力和刚度与操作员的力和刚度相结合，以评估末端点的力和刚度。

5. 手臂定义外骨骼控制律

本研究的主要目的是开发一个手臂模型，以评估外骨骼的控制律（图2中的“控制律”模块）。

5.1. 手臂肌腱系统模型

手臂模型由两个代表肱骨和桡尺骨的刚性段组成。它们通过一个对应于肘部的单自由度铰链连接。

两个执行器模拟作用在关节上的肱桡肌（BRD，肌肉1）和肱三头肌外侧头（TriLat，肌肉2）（图3）。

示意图2

连杆与执行器之间通过铰链连接。假设当前臂完全伸展时，肘关节角度α为零，并随着肘关节屈曲而增大。

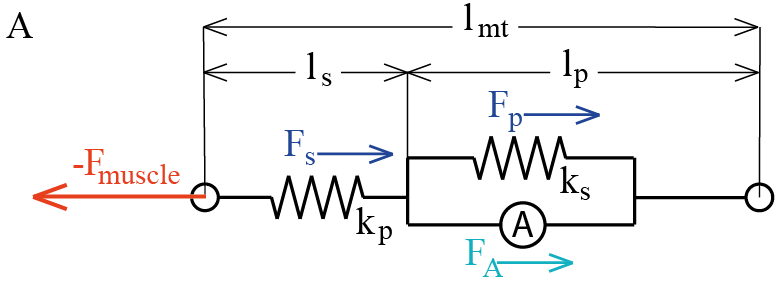
执行器为单作用：仅施加相互对抗的拉力作用，并作为冗余驱动[39, 40]工作。肌腱系统基于希尔模型进行解析描述，该模型在计算文献中较为常见，是分析可行机械行为的有效方法。希尔模型[41]由不同的元件组成（图4A）。

示意图3

肌肉（lp）由一个主动元件（A）和一个与A并联的非线性弹簧（并联弹簧）组成，其中主动元件表示肌动蛋白‐肌球蛋白作用，并联弹簧用于模拟胶原组织。

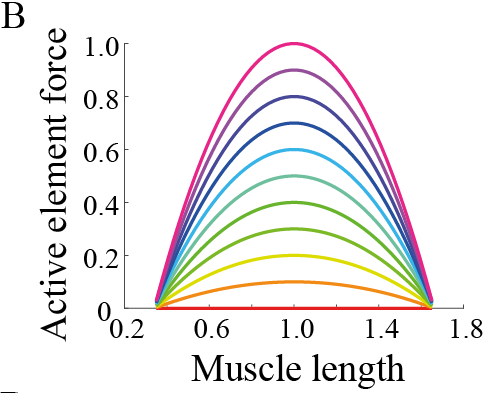
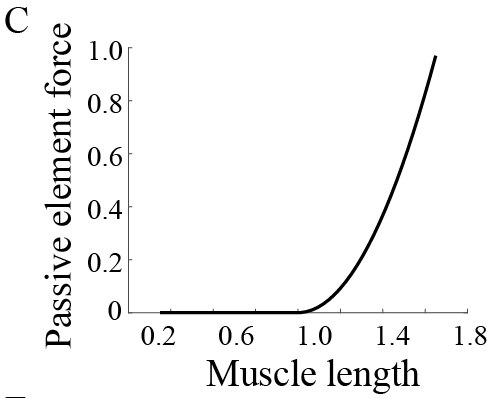
肌腱段（ls）由一个与A串联的非线性弹簧（串联弹簧）构成。主动元件施加的力（FA）和并联弹簧施加的力（Fp）与肌肉段长度（lp）之间的关系定律，以及串联弹簧施加的力（Fs）与肌腱长度（ls）之间的关系定律及其系数，均在引自文献[42, 43]的公式(1)–(3)（Figs. 4B–D）中给出。

$$ FA = m \cdot F_{MAX}[-a(l_p / l_{ce})^2 + 2a (l_p / l_{ce}) - a + 1] \tag{1} $$

$$ F_s = k_s[\max(0, l_s - l_{s0})]^2 \tag{2} $$

$$ F_p = k_p[\max(0, l_p / l_{ce} - l_{p0} / l_{ce})]^2 \tag{3} $$

其中 $ a = 1/w^2 $，w为肌肉宽度；m为肌肉激活度，以最大自主收缩（MVC）的分数表示；$ l_{ce} $为肌肉产生最大主动力（$ F_{MAX} $）时的最优长度；$ k_p $为肌肉刚度（选择使得当 $ F_p = F_{MAX} $ 时，比值 $ l_p / l_{ce} = 1+w $）；$ l_{p0} = l_{ce} $为肌肉松弛长度，表示并联弹簧不产生被动力时肌肉的最大长度；$ k_s $为腱刚度（选择使得在 $ F_{MAX} $ 时，$ l_s = 1.04l_{s0} $[44]）；$ l_{s0} $为肌腱松弛长度，表示串联弹簧不产生任何力时肌腱的最大长度。$ F_{MAX} $、$ l_{ce} $ 和 $ l_{s0} $ 为肌肉特异性参数。与BRD和TriLat[45]相关的特征值及人体测量信息见表1。

参数	BRD (肌肉1)	TriLat (肌肉2)
$ l_{ce} $ [m]	0.0858	0.1138
$ l_{p0} $ [m]	0.0858	0.1138
$ l_{s0} $ [m]	0.0535	0.0980
$ F_{max} $ [N]	261.33	624.3
$ k_p $ [N/m]	600	1433
$ k_s $ [N/m]	163×10³	390×10³
附着于桡骨‐尺骨 [m]	l₁₁：0.1274	l₂₁：0.0219
肱骨上的附着点 [m]	l₁₂：0.1004	l₂₂：0.1735

图4B–D 是肌肉的主动元件、并联弹簧和串联弹簧在不同激活水平下，其施加的力与长度关系的曲线图。图4E 展示了肌肉元件的施加的力与其长度的关系，而图4F 描述肌肉‐肌腱系统在其长度上的受力情况。

5.2. 力平衡方程

假设关节旋转轴为垂直方向，以忽略重力作用。

方程 (4) 描述了动态平衡：

$$
\begin{cases}
F_{s1} = F_{p1} + F_{A1} \
F_{s2} = F_{p2} + F_{A2} \
m a_2 (F_{p2} + F_{A2}) = m a_1 (F_{p1} + F_{A1})
\end{cases}
\tag{4}
$$

其中 $ F_{si} $、$ F_{pi} $、$ F_{Ai} $ 和 $ m a_i $ 分别表示串联弹簧、并联弹簧、主动元件以及肌力力臂相对于肘部产生的力。两条肌肉用 i = 1,2 表示。

力方程与几何方程耦合，如下所示：

$$
\begin{cases}
l_{mti} = l_{pi} + l_{si} \
l_{mti} = \sqrt{l_{i1}^2 + l_{i2}^2 - 2 \cdot l_{i1} \cdot l_{i2} \cdot \cos \beta_i} \
m a_i = \frac{2}{l_{mti}} \sqrt{P_i (P_i - l_{i1})(P_i - l_{i2})(P_i - l_{mti})}
\end{cases}
\tag{5}
$$

5.3. 刚度与性能计算

根据不同水平的肌肉1激活来定义共收缩程度。

肌腱系统的旋转刚度定义为施加扭矩 $ \tau_i $ 所引起的位移导数：

$$
K_i = m a_i \frac{\partial (F_{pi} + F_{Ai})}{\partial \alpha} + (F_{pi} + F_{Ai}) \frac{\partial m a_i}{\partial \alpha} \tag{6}
$$

在正负方向上对肘关节施加一个小的偏转（ $ \partial \alpha = 0.01^\circ $ ）[10]，同时保持肌肉激活水平不变。方程 (6) 表示特定姿势下肘关节刚度的估计。

肌肉施加的力取决于其长度，并在肘关节处产生相应的扭矩。肘关节角度‐扭矩关系可在未受扰动状态下进行线性化，其斜率代表肌肉的刚度。肘部的旋转刚度是肘关节角度‐扭矩关系曲线斜率之差。肌肉1相对于肌肉2的角度‐扭矩曲线。性能计算为系统输出（即肘部刚度）与模型输入（即肌肉激活的范数）之间的比值。

6. 模型分析

6.1. 肌腱系统特性

关节角度的变化导致拮抗肌长度产生不同的变化。由于每块肌肉的扭矩‐长度特性是特定的，这种行为可被理解为一块肌肉的特性相对于另一块肌肉发生偏移，以匹配两块肌肉在特定关节角度下的长度（图5）。我们可以观察到，这种偏移使得两块肌肉能够在相同的角度范围（20°和130°之间）施加力，即使它们在不同的长度范围（肌肉1为0.09至0.20米，肌肉2为0.17至0.21米）内产生力。

示意图4

6.2. 肘关节角度边界

由于生理边界，肘部可达到的角度范围如[46]所示。然而，由于肌肉力的施加特性，可能存在其他边界。因此，生理边界与肌肉特性导致的边界可能并不一致。在图6A中，由于生理边界的存在，肘关节屈曲的上限值被固定在130°。

然而，对于较高的肘关节屈曲值，也可以获得共收缩的可能解。然而，现有研究确定的下限接近0°，尽管在20°以下，本模型中两块肌肉特性之间不可能存在交点。这种差异可能是由于肌肉模型的近似所致，或因为该模型忽略了作用于同一肘关节的其他肌肉。

可以观察到，如果肘关节未施加扭矩，则拮抗肌的激活水平唯一地确定了肘关节屈曲。

示意图5

6.3. 拮抗肌肉激活

在图6B中，为确保肘关节处的平衡，肌肉2的激活水平在不同的肘关节构型和肌肉1激活情况下被表示出来。关于肌肉1低激活的曲线相比肌肉1高激活的曲线更为稀疏。因此，在本图及后续图中，肌肉1激活之间的步长并不恒定。当角度低于85°时，可能出现随遇平衡，此时两种肌肉均保持无激活状态。

激活肌肉2对于肘部屈曲角度高于85°的情况始终是必要的，以补偿肌肉1的被动元件所施加的力。

并非所有可能的肘关节屈曲和肌肉1激活水平都可以同时实现。特别是，只有在肘关节屈曲值较高时，肌肉1的高激活水平才能由肌肉2来平衡。而肌肉2的低激活水平仅在肘关节屈曲值较低时才能由肌肉1来平衡。

这些边界定义了一个肌肉激活范围，在此范围内可以在不施加扭矩的情况下实现肘部的刚性增强。

6.4. 手臂刚度

图7A中展示了两块肌肉的刚度。虽然肌肉2的刚度始终为非负值，但肌肉1的刚度可能呈现负值。这种行为在生理上是可能的，其原因是肘关节屈曲‐力矩关系的负斜率（见图6A），这导致肌腱系统长度增加时产生的力矩减小。

示意图6

关节刚度随每个肘关节角度下的肌肉激活水平增加而增加（图7B）。由于肌肉1的被动和主动元件的存在，可以观察到两个峰值。由于肌肉1在高激活状态下产生的扭矩只能在某些关节角度下达到平衡，因此较高肌肉激活水平的刚度仅可在这些角度下计算。存在一些肘关节屈曲角度，在这些角度下两块肌肉均未被激活。在这些情况下，可找到一个刚度为零的角度范围。

6.5. 性能

性能定义为肘关节刚度与肌肉激活范数之间的比值（图8），在70°和90°之间出现最小值。这些最小值依赖于肌肉激活水平，并出现在肌肉1的并联弹簧开始作用时对应的关节角度处。除肌肉激活为零的情况外，存在两个峰值。第一个峰值对应于肌肉1的并联弹簧施加被动力时的关节角度（较低的关节角度）。第二个峰值对应于肌肉1的并联弹簧不施加任何力时的关节角度（较高的关节角度）。因此，我们可以找到一个系统在增加关节刚度方面更有效的范围。

示意图7