GAN入门实践
一、题目介绍
题目链接:Use GANs to create art - will you be the next Monet?
我们通常通过艺术家的独特风格来识别他们的作品,例如颜色选择或笔触。生成对抗网络(GAN)现在可以用算法模仿像莫奈这样的艺术家的作品。在这个题目中,将尝试把这种风格带到照片中,或者从零开始创造这种风格!
GAN 现在能够以非常令人信服的方式模仿物体,但创造博物馆级的杰作被认为是艺术而非科学。那么科学能否以 GAN 的形式欺骗分类器,让他们相信你创造了一个真正的莫奈?
二、GAN介绍
GAN 至少由两个神经网络组成:一个生成器模型和一个判别器模型。生成器是创建图像的神经网络,生成器使用鉴别器进行训练。
这两个模型将相互对抗,生成器试图欺骗鉴别器,而鉴别器试图准确地对真实图像和生成的图像进行分类。

生成器G和判别器D的相同点是:
- 这两个模型都可以看成是一个黑匣子,接受输入然后有一个输出,类似一个函数,一个输入输出映射。
其不同点是:
- 生成模型功能:比作是一个样本生成器,输入一个样本,然后通过他生成另一个样本。
- 判别模型:用以判断生成的样本和真实目标之间的差距。
三、CycleGAN
3.1 模型介绍
Cycle GAN是Jun-Yan Zhu等人提出的图像-图像转换对抗网络。图像-图像转换问题的目标是学习一种从源域到目标域的转换 G : X → Y G:\ X\rightarrow Y G: X→Y,使得在判别器上X和Y的分布不可区分。
但是,这种映射往往会是欠约束的,所以作者使用了另一个新的映射 F : G ( X ) → X F:\ G(X) \rightarrow X F: G(X)→X与映射G耦合,来实现模型训练的一致性。这种方法来自语言翻译中的“循环一致”原则:从中文翻译成英文的句子,反义会中文,应当回到原始的句子。
3.2 算法架构
其结构示意图如下所示:
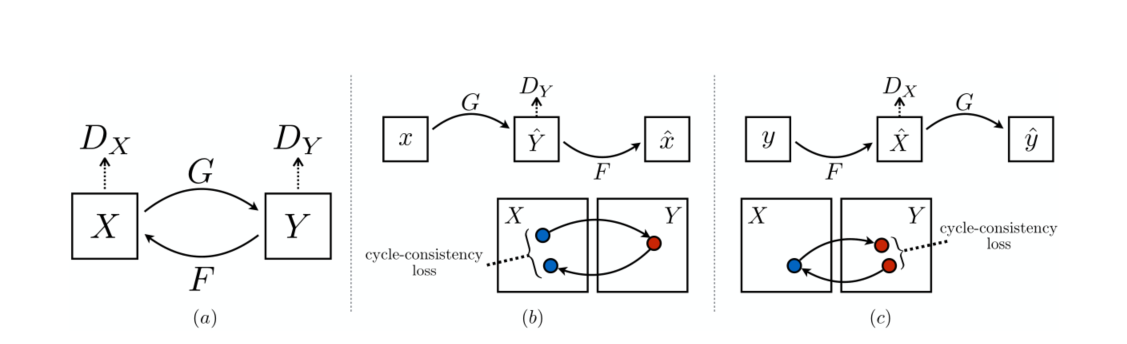
模型包括两个生成器 G G G和 F F F,和与其相关的判别器 D Y D_Y DY和 D X D_X DX
- G : X → Y G:\ X\rightarrow Y G: X→Y
- F : Y → X F:\ Y\rightarrow X F: Y→X
- Y ^ = G ( X ) , X ^ = F ( Y ) \hat{Y} = G(X),\ \ \ \hat{X}=F(Y) Y^=G(X), X^=F(Y)
- D Y : L o s s ( Y ^ , Y ) D_Y:\ Loss(\hat{Y}, Y) DY: Loss(Y^,Y)
- D X : L o s s ( X ^ , X ) D_X:\ Loss(\hat{X}, X) DX: Loss(X^,X)
- 正向一致性损失: L o s s ( X , F ( Y ^ ) ) = L o s s ( X , F ( G ( X ) ) ) Loss(X, F(\hat{Y}))=Loss(X,F(G(X))) Loss(X,F(Y^))=Loss(X,F(G(X)))
- 反向一致性损失: L o s s ( Y , F ( X ^ ) ) = L o s s ( Y , G ( F ( Y ) ) ) Loss(Y, F(\hat{X}))=Loss(Y,G(F(Y))) Loss(Y,F(X^))=Loss(Y,G(F(Y)))
3.3 优化目标
经典的GAN采用负对数似然(NLL)来作为优化目标:
- 对于生成器G: L g = − E x ∼ p d a t a ( x ) ∣ log ( 1 − D ( G ( x ) ) ∣ L_g=-\mathbb{E}_{x\sim p_{data}(x)}|\log{(1-D(G(x))}| Lg=−Ex∼pdata(x)∣log(1−D(G(x))∣
用以最小化生成样本的“判别结果为真的样本”(判别器对真实目标输出为1,假目标为0)间的差距。 - 对于判别器D: L d = − E x ∼ p d a t a ( x ) ∣ log D ( G ( x ) ) ∣ + − E y ∼ p d a t a ( y ) ∣ log ( 1 − D ( y ) ) ∣ L_d=-\mathbb{E}_{x\sim p_{data}(x)}|\log{D(G(x))}|+-\mathbb{E}_{y\sim p_{data}(y)}|\log{(1-D(y))}| Ld=−Ex∼pdata(x)∣logD(G(x))∣+−Ey∼pdata(y)∣log(1−D(y))∣
其中前半部分最小化生成样本和“判别为假的样本”(即判别器输出0的样本)的距离,后半部分最小化对目标样本和“判别结果为真的样本”的距离。前半部分用于对抗生成器G,后半部分用于提示判别能力。
在CycleGAN中,我们将负对数似然改为最小二乘损失,这种损失在训练期间更稳定,并产生更高质量的结果。在优化生成器G的时候引入循环一致性损失 L c y c L_{cyc} Lcyc和同一性损失 L i d e n t i t y L_{identity} Lidentity作为正则化项。
- L G = E x ∼ p d a t a ( x ) [ ( 1 − D Y ( G ( x ) ) ) 2 ] L_{G}=\mathbb{E}_{x\sim p_{data}(x)}[(1-D_Y(G(x)))^2] LG=Ex∼pdata(x)[(1−DY(G(x)))2]
- L F = E y ∼ p d a t a ( y ) [ ( 1 − D X ( F ( y ) ) ) 2 ] L_{F}=\mathbb{E}_{y\sim p_{data}(y)}[(1-D_X(F(y)))^2] LF=Ey∼pdata(y)[(1−DX(F(y)))2]
- L D Y = E x ∼ p d a t a ( x ) [ D ( G ( x ) ) 2 ] + E y ∼ p d a t a ( y ) [ ( 1 − D ( y ) ) ) 2 ] L_{D_Y}=\mathbb{E}_{x\sim p_{data}(x)}[D(G(x))^2]+\mathbb{E}_{y\sim p_{data}(y)}[(1-D(y)))^2] LDY=Ex∼pdata(x)[D(G(x))2]+Ey∼pdata(y)[(1−D(y)))2]
- L D X = E y ∼ p d a t a ( y ) [ D ( F ( y ) ) 2 ] + E x ∼ p d a t a ( x ) [ ( 1 − D ( x ) ) ) 2 ] L_{D_X}=\mathbb{E}_{y\sim p_{data}(y)}[D(F(y))^2]+\mathbb{E}_{x\sim p_{data}(x)}[(1-D(x)))^2] LDX=Ey∼pdata(y)[D(F(y)





 本文介绍了如何利用生成对抗网络(GAN)中的CycleGAN技术,将照片转化为类似莫奈画作的艺术风格。CycleGAN通过两个相互作用的生成器和判别器,实现图像之间的无监督转换,同时保持内容的一致性。在PyTorch中实现CycleGAN,包括数据集准备、模型结构、训练和优化过程,以及最终的效果展示,展示了科学如何借助GAN创造出艺术效果。
本文介绍了如何利用生成对抗网络(GAN)中的CycleGAN技术,将照片转化为类似莫奈画作的艺术风格。CycleGAN通过两个相互作用的生成器和判别器,实现图像之间的无监督转换,同时保持内容的一致性。在PyTorch中实现CycleGAN,包括数据集准备、模型结构、训练和优化过程,以及最终的效果展示,展示了科学如何借助GAN创造出艺术效果。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 2103
2103

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










