生成模型与判别模型的区别
判别模型的学习算法学习给定x下的条件分布p(y|x; θ),
例如,Logistic Regression(对数几率回归)将p(y|x; θ)建模为,g是sigmoid函数。
考虑一个分类问题,基于动物的某些特征想要区分大象(y=1)和狗狗(y=0)。给定一个数据集,类似LR或者感知机的算法尝试找到一条直线(超平面),也就是决策边界,将大象和狗狗分开。然后,当新样本要将其分类为大象类和狗狗类时,只需要检查新样本落在决策边界的哪一边,然后再对新样本进行预测。
这篇博客要谈的是另外一类学习算法,与上面的方法不同,首先看大象,构建一个大象长什么样子的模型,然后看狗狗,构建一个狗狗长什么样的分离模型,最后当输入一个新动物时,将这个新动物与大象模型和狗狗模型分别进行匹配,看新动物是更像大象还是更像狗狗。
直接学习p(y|x)或者尝试学习到一个从输入空间到输出标签{0,1}的映射(例如感知机算法)的学习算法叫做判别学习算法,这样的模型叫做判别模型。
生成式学习算法与判别式算法不同,它尝试对p(x|y)和p(y)进行建模,例如,如果y表示一个样本是狗狗(y=0)或者大象(y=1),则p(x|y=0)对狗狗的特征分布进行建模,p(x|y=1)对大象的特征进行建模。
当建模了p(y)(类先验)和p(x|y),可以使用贝叶斯公式导出给定x时y的后验分布:
预测的时候:

高斯判别分析模型(GDA)
当输入特征x是连续值的随机变量,可以使用高斯判别分析(Gaussian Discriminant Analysis, GDA),GDA使用多维正态分布对p(x|y)进行建模,模型如下:
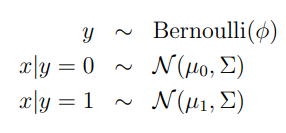
写成分布的形式:
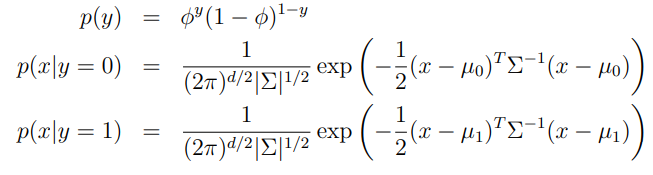
模型的参数是 ,
,
和
,均值向量不同,协方差矩阵相同。
对数似然:
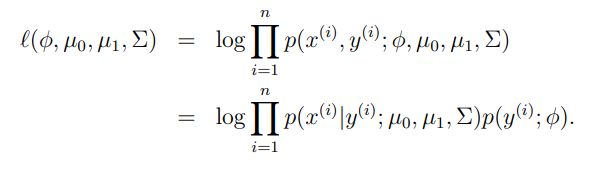
通过最大似然估计其参数如下:
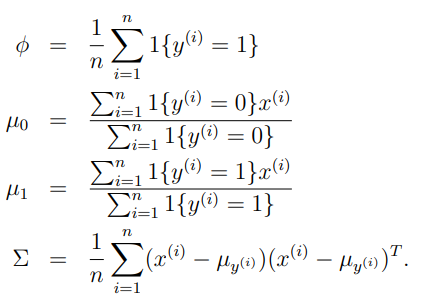
算法的分类效果如下:
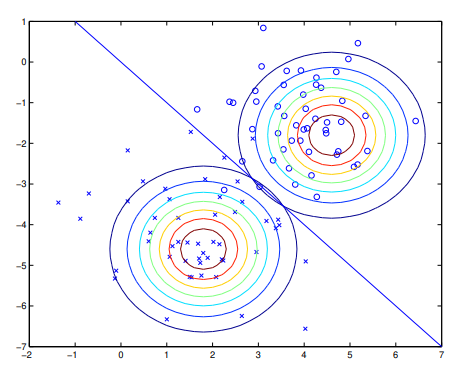
使用两个高斯分布来拟合两个类的数据,这两个高斯的等高线有相同的形状和方向,因为它们的协方差相同。这两个高斯的均值不同。
朴素贝叶斯
在GDA中,特征向量x是连续的实数,当特征向量的值是离散时可以使用贝叶斯模型。例如,如果想使用机器学习做一个垃圾邮件过滤器,将邮件信息分类为垃圾广告邮件和非垃圾邮件。我们有一个训练集(带标签的数据),特征向量的长度等于词典的长度,如果一个邮件包含第j个单词,则这个特征设置为1;否则,设置为0。例如,一个样本邮件的特征向量如下:
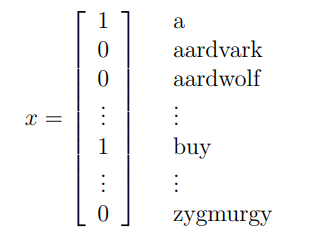
有了特征向量,我们构建一个生成模型来对p(x|y)来建模。假定在给定的y下条件独立,这个假设成为贝叶斯假设,对应的算法成为贝叶斯分类器。
tips:
- 第2087个特征x2087和第39831个特征条件独立可以写成:
p(x2087|y) = p(x2087|y, x39831)
表示当y给定的情况下,知道x39831与否对知道x2087的概率没有影响。
- 第2087个特征和第39831个特征独立可以写成
p(x2087) = p(x2087|x39831)
后验分布p(x|y)可以写成: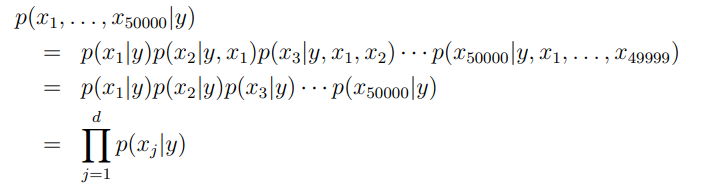
联合似然:
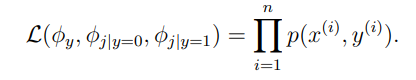
最大似然估计后的参数:
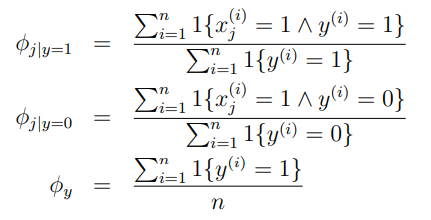
对新样本进行预测:
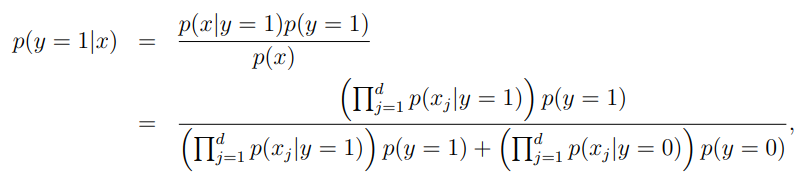





 本文探讨了生成模型与判别模型的区别。生成模型学习p(x|y)和p(y),如高斯判别分析和朴素贝叶斯,而判别模型直接学习p(y|x),如逻辑回归。生成模型试图构建输入和输出的联合分布,而判别模型关注输入到输出的映射。在分类问题中,这两种方法分别有不同的应用策略。
本文探讨了生成模型与判别模型的区别。生成模型学习p(x|y)和p(y),如高斯判别分析和朴素贝叶斯,而判别模型直接学习p(y|x),如逻辑回归。生成模型试图构建输入和输出的联合分布,而判别模型关注输入到输出的映射。在分类问题中,这两种方法分别有不同的应用策略。
















 4681
4681

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








