Minimum Sum 完善划分树

Minimum Sum

Time Limit: 16000/8000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 1152    Accepted Submission(s): 263

Problem Description

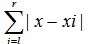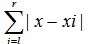You are given N positive integers, denoted as x0, x1 ... xN-1. Then give you some intervals [l, r]. For each interval, you need to find a number x to make   as small as possible!

Input

The first line is an integer T (T <= 10), indicating the number of test cases. For each test case, an integer N (1 <= N <= 100,000) comes first. Then comes N positive integers x (1 <= x <= 1,000, 000,000) in the next line. Finally, comes an integer Q (1 <= Q <= 100,000), indicting there are Q queries. Each query consists of two integers l, r (0 <= l <= r < N), meaning the interval you should deal with.

Output

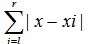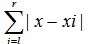For the k-th test case, first output “Case #k:” in a separate line. Then output Q lines, each line is the minimum value of   . Output a blank line after every test case.

 

Sample Input

  

   2

5
3 6 2 2 4
2
1 4
0 2

2
7 7
2
0 1
1 1
  

 

Sample Output

  

   Case #1:
6
4

Case #2:
0
0
  

 

Author

standy

 

Source

2010 ACM-ICPC Multi-University Training Contest（4）——Host by UESTC

这个不同于POJ的Kth Number，比它要注意的几点是：

1、它的数值序列式允许重复的，因此需要解决

2、需要统计和

解题思路：这一题很久一前就见过，不过不会做。因为当时不会划分树，我们可以很容易的看出找到中位数，在统计中位数两边的和即可

这里我们统计总和和一边的和，拿总的减去一边便是另一边。这里我颠覆来原来看似简洁的写法，原来那个边界考虑的很多，容易糊涂

这里为了简单改写为另一种写法，就是行布朗当的把从一开始的所有和均统计出来，我们从一开始，0号元素为0，那么就不会影响结果。

所有区间的统计均是末减初 （前提是先序遍历，你懂得），这样统计某一区间时，直接减即可。

第一种写法代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;
const int MAX = 100002;
const int MAX_depth = 32;
int val[MAX_depth][MAX];
int a[MAX_depth][MAX];
long long sum[MAX_depth][MAX];
int s[MAX];


void Build(int l, int r, int depth) {
    if (l == r) {
        sum[depth][l] = val[depth][l];
        return;
    }
    int mid = (l + r) / 2;
    int same = mid - l + 1;
    for (int i = l; i <= r; i++) {
        if (val[depth][i] < s[mid]) {
            same--;
        }
    }
    int lc = l;
    int rc = mid + 1;
    for (int i = l; i <= r; i++) {
        if (i == l) {
            sum[depth][i] = val[depth][i];
        } else {
            sum[depth][i] = sum[depth][i - 1] + val[depth][i];
        }


        if ((val[depth][i] < s[mid]) || (val[depth][i] == s[mid] && same > 0)) {
            if (val[depth][i] == s[mid]) same--;
            if (i == l) {
                a[depth][i] = 1;
            } else {
                a[depth][i] = a[depth][i - 1] + 1;
            }
            val[depth + 1][lc++] = val[depth][i];
        } else {
            if (i == l) {
                a[depth][i] = 0;
            } else {
                a[depth][i] = a[depth][i - 1];
            }
            val[depth + 1][rc++] = val[depth][i];
        }
    }
    Build(l, mid, depth + 1);
    Build(mid + 1, r, depth + 1);
}

long long total;
int pre_same;

int Search(int s, int e, int l, int r, int k, int depth) {
    if (l == r) {
        return val[depth][l];
    }
    int mid = (l + r) / 2;
    int So = a[depth][s - 1];
    if (s == l) {
        So = 0;
    }
    int x = a[depth][e] - So;
    if (x >= k) {
        return Search(l + So, l + a[depth][e] - 1, l, mid, k, depth + 1);
    } else {
        pre_same += x;
        if (a[depth][e] > 0) {
            total += sum[depth + 1][l + a[depth][e] - 1];
            if (So > 0) {
                total -= sum[depth + 1][l + So - 1];
            }
        }
        return Search(mid + 1 + s - l - So, mid + 1 + e - l - a[depth][e], mid + 1, r, k - x, depth + 1);
    }
}

int main() {
    int n, m;
    int T;
    scanf("%d", &T);
    for (int k1 = 1; k1 <= T; k1++) {
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) {
            scanf("%d", &val[0][i]);
            s[i] = val[0][i];
        }

        sort(s + 1, s + n + 1);
        Build(1, n, 0);
        int s, e;
        scanf("%d", &m);
        printf("Case #%d:\n", k1);
        for (int i = 0; i < m; i++) {
            scanf("%d%d", &s, &e);
            s++, e++;
            int k = (e - s + 2) / 2;
            total = 0;
            pre_same = 0;
            long long x = Search(s, e, 1, n, k, 0);
            long long All = sum[0][e];
            if (s > 1) {
                All -= sum[0][s - 1];
            }
            long long result = pre_same * x - total + All - total - (e - s + 1 -pre_same) * x;
           cout<<result<<endl;
        }
        printf("\n");
    }
    return 0;
}

第二种写法：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAX_depth = 33;
const int MAX = 100010;
int to_left[MAX_depth][MAX];
int val[MAX_depth][MAX];
long long sum[MAX_depth][MAX];
int s[MAX];
long long sum1[MAX];


/*明白了思想，其实没必要每段都算，其实是给自己制造麻烦，累加即可*/
void Build(int left, int right, int depth) {
    if (left == right)return;
    int mid = (left + right) >> 1;
    int same = mid - left + 1;
    for (int i = left; i <= right; i++) {
        if (val[depth][i] < s[mid]) {
            same--;
        }
    }
    int lc = left, rc = mid + 1;
    for (int i = left; i <= right; i++) {
        if ((val[depth][i] < s[mid]) || (val[depth][i] == s[mid] && same > 0)) {
            if (val[depth][i] == s[mid])same--;
            val[depth + 1][lc++] = val[depth][i];
            to_left[depth][i] = to_left[depth][i - 1] + 1;
            sum[depth][i] = sum[depth][i - 1] + val[depth][i];
        } else {
            val[depth + 1][rc++] = val[depth][i];
            to_left[depth][i] = to_left[depth][i - 1];
            sum[depth][i] = sum[depth][i - 1];
        }
    }
    Build(left, mid, depth + 1);
    Build(mid + 1, right, depth + 1);
}


long long left_sum;
int lnum;

int Search(int start, int end, int left, int right, int k, int depth) {
    if (left == right) return val[depth][left];
    int mid = (left + right) >> 1;
    int s = to_left[depth][start - 1] - to_left[depth][left - 1];
    int e = to_left[depth][end] - to_left[depth][left - 1];
    int x = to_left[depth][end] - to_left[depth][start - 1];
    int rs = start - left - s; /*[left,start-1]*/
    int re = end - left + 1 - e; /*[left,end]*/
    if (x >= k) {
        return Search(left + s, left + e - 1, left, mid, k, depth + 1);
    } else {
        lnum += x;
        left_sum += sum[depth][end] - sum[depth][start - 1];
        return Search(mid + 1 + rs, mid + 1 + re - 1, mid + 1, right, k - x, depth + 1);
    }
}

int main() {
    int n, m;
    int T;
    while (scanf("%d", &T) != EOF) {
        for (int cas = 1; cas <= T; cas++) {
            scanf("%d", &n);
            for (int i = 0; i < 33; i++) {
                sum[i][0] = 0;
                to_left[i][0] = 0;
            }
            sum1[0] = 0;
            for (int i = 1; i <= n; i++) {
                scanf("%d", &val[0][i]);
                s[i] = val[0][i];
                sum1[i] = sum1[i - 1] + s[i];
            }
            sort(s + 1, s + n + 1);
            Build(1, n, 0);
            scanf("%d", &m);
            printf("Case #%d:\n", cas);
            int s, e;
            for (int i = 0; i < m; i++) {
                scanf("%d%d", &s, &e);
                s++;
                e++;
                lnum = 0;
                left_sum = 0;
                int k = (e - s) / 2 + 1;
                long long x = Search(s, e, 1, n, k, 0);
                long long all = sum1[e] - sum1[s - 1];
                long long res = lnum * x - left_sum + all - left_sum - (e - s + 1 - lnum) * x;
                cout<<res<<endl;
            }
            printf("\n");
        }
    }
    return 0;
}