夜深人静写算法——01背包（动态规划）

01背包：

    一：
　　01背包问题需要求解的就是，体积V的背包中物体总价值最大化，第N件物品中第i件是否要放入背包中？（其中每个物品最多只能放一件） ( 物品体积为w[i],物品价值为v[ i ] ) ;

    二：

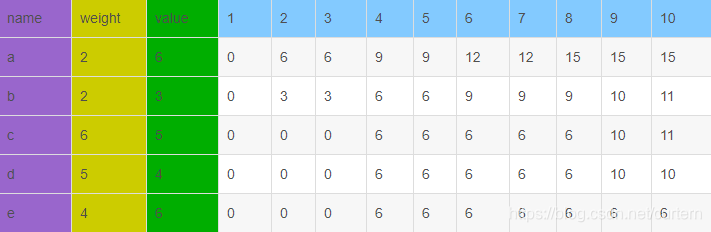
       定义二维数组 dp[ i ][ j ]表示当前背包大小为 j 时，对于第 i 件物品的最优解（可能放入，也可能不放入）； 

       动态规划方程：

       (1)   j < w[ i ] :  dp[ i][ j ] = dp[ i  + 1][ j ] (背包体积不够, 物品不放入，跳到下一个物品的最优解）；

       (2)  j >= w[i] :  dp[ i ][ j ] = max(dp[ i + 1][j - w[ i ]] + v[i], dp[i + 1][ j ]); (如果把物品放入背包，背包体积变成 j - w[i] )

    三：
　  

  

#include <iostream>
#include <algorithm> 
#include <string