算法 | 生命游戏 (Game of Life)

概要： 本文将要介绍一个名为“生命游戏”的有趣算法并用C++进行简单的实现。
关键字： C++;生命游戏算法
 

1 背景说明

   生命游戏，又叫康威生命游戏(Conway’s Game of Life)，或康威生命棋，是英国数学家约翰·康威(John Conway)在1970年发明的细胞自动机。它最初在1970年10月在《科学美国人》杂志上的“数学游戏”专栏出现。我大一暑假在上暑期课程时无意中接触到这个概念，并被它看似简单的外表、实则复杂的“内心”所吸引，于是出于好奇就自己用C++模拟了一翻，直到最近整理本科成果时又一次翻到了这个小巧有趣的代码。代码很短，只有一二百行，其中核心的判断和计算的部分只有十来行；其算法更是简单，几句话就可以描述清楚。下面我将做简要的介绍。

2 算法原理

2.1 概述

   生命游戏是一个零玩家游戏。它发生在一个二维矩形世界，这个世界的基本组成单位是一个一个等大的小方格。每个方格居住着一个活着的或死了的细胞。一个细胞在下一个时刻生死取决于相邻八个方格中活着的细胞的数量。一方面，如果相邻方格活着的细胞数量过多，这个细胞会因为资源匮乏而在下一个时刻死去；另一方面，如果周围活细胞过少，这个细胞会因太孤单而死去。而只有其周围的细胞数量适合时，这个方格中的细胞才能继续存活。若方格中原来的细胞已经死亡，在其周围细胞数量合适时，也会使得该死细胞“死而复生”，这可以认为是在模拟细胞的繁殖。玩家可以设定周围活细胞的数目怎样时才事宜细胞生存和繁殖。但是需要注意的是，如果这个数目设定过高，世界中的大部分细胞会因为找不到太多的活的邻居而死去，直到整个世界都没有生命；如果这个数目设定过低，世界中又会被生命充满而没有什么变化。

   实际游戏中，这个数目一般选取2或者3；这样整个生命世界才不至于太过荒凉或拥挤，而是出于一种动态平衡之中。如此一来，游戏的规则就是：当一个方格周围有2或3个活细胞时，方格中的活细胞在下一个时刻继续存活；即使这个时刻方格中没有活细胞，在下一个时刻也会“诞生”活细胞。否则，这个方格中的细胞会死亡，或不诞生新的活细胞。

2.2 规则

   在选取了合适的数据后，对具体规则作如下描述。

   生命游戏中，对于任意细胞：
   每个细胞有两种状态：存活或死亡。每个细胞与以自身为中心的周围八格细胞产生互动。
   1.当前细胞为存活状态时，当周围的活细胞低于2个时， 该细胞因孤独而死亡;
   2.当前细胞为存活状态时，当周围有2个或3个活细胞时， 该细胞保持原样;
   3.当前细胞为存活状态时，当周围有3个以上活细胞时，该细胞因资源匮乏而死亡;
   4.当前细胞为死亡状态时，当周围有3个活细胞时，该细胞变成存活状态(模拟繁殖)。

3 程序实现

   我用C++模拟了上述过程。此算法的核心在于计算下一代细胞的存亡图景，代码如下所示:

void NextG(int p[][MAXLIS],int q[][MAXLIS])               
{
	int i,j,x,y;
	int judge;
	for(i = 0;i < MAXROW;i++)
	{
		for(j = 0;j < MAXLIS;j++)
		{
			if(p[i][j] == ALIVE)
			{
				judge = -1;                         //每一轮结束judge都要复位
			}
			else if(p[i][j] == DEAD)
			{
				judge = 0;
			}
			for(x = MAX(i-1,0);x<=MIN(i+1,MAXROW-1);x++)     //开始这里的MAXROW和MAXLIS后面忘记-1，逻辑出错找了好久
			{
				for(y = MAX(j-1,0);y<=MIN(j+1,MAXLIS-1);y++)
				{
					if(p[x][y] == ALIVE)
						judge +=1;
				}
			}
			switch(judge)
			{
			case 2:q[i][j] = p[i][j];break;			// 周围有2个活细胞，保持原样
			case 3:q[i][j] = ALIVE;break;			// 周围有3个活细胞，生则继续，死则复活(模拟繁殖)
			default:q[i][j] = DEAD;break;			// 周围有1或4-8个活细胞，死(模拟拥挤而死或孤独而死)
			}
		}
	}
}

   代码本身可以说是相当简单了，学过数组的人都能写出来。剩下的就是一些装饰门面的活儿，比如说我当时写的测试代码——即main()函数——是长这个样子的:

int main()
{
	int CHOICE = 1,n = 0;
	int choice;
	int map[MAXROW][MAXLIS] = {DEAD},newmap[MAXROW][MAXLIS] = {DEAD};		//定义2个同维数组并初始化为全0数组	
	cout<<"_________________________________________"<<endl;
	cout<<"|                                        |"<<endl;
	cout<<"|    欢迎来到“生命游戏”！                  |"<<endl;
	cout<<"|                                        |"<<endl;
	cout<<"|    请选择初始化模式：                    |"<<endl;
	cout<<"|                                        |"<<endl;
	cout<<"|       1.自动模式A     2.自动模式B        |"<<endl;
	cout<<"|                                        |"<<endl;
	cout<<"|       3.随机模式      4.手动模式         |"<<endl;
	cout<<"|________________________________________|"<<endl;
	cin>>choice;
	switch(choice)
	{
	case 1:Init1(map);break;               //二维数组作为函数参数被调用时，参数是二维数组的起始位指针，也就是数组名
	case 2:Init2(map);break;
	case 3:Init3(map);break;
	case 4:Init4(map);break;
	default:
		{
			cout<<"默认为随机初始化模式."<<endl;
			Init3(map);
			break;
		}
	}            
	cout<<endl<<"父代细胞生存图："<<endl;
	ShowMap(map);
	while(CHOICE)
	{
		NextG(map,newmap);
		CopyClc(map,newmap);
		cout<<endl<<"子"<<n++<<"代细胞生存图："<<endl;
		ShowMap(map);
		cout<<"\n继续请按除0以外的任意数字键."<<endl;
		cin>>CHOICE;
	}
	cout<<"您已退出游戏."<<endl;
	return 0;
}

   这里我给出了4种初始化的条件供用户选择，同时为了让用户看清中间的每一个步骤，我让用户自己步进操作，也省了设置步进时长的麻烦，当然这些都是小细节。另外，很多人直接把这个例程写在了网页上，大家也可以去感受一下，推荐的网址有链接1和链接2。

4 结果分析

   代码跑通之后就可以随意玩耍了！运行的界面如图1所示：

图1 程序运行界面

 
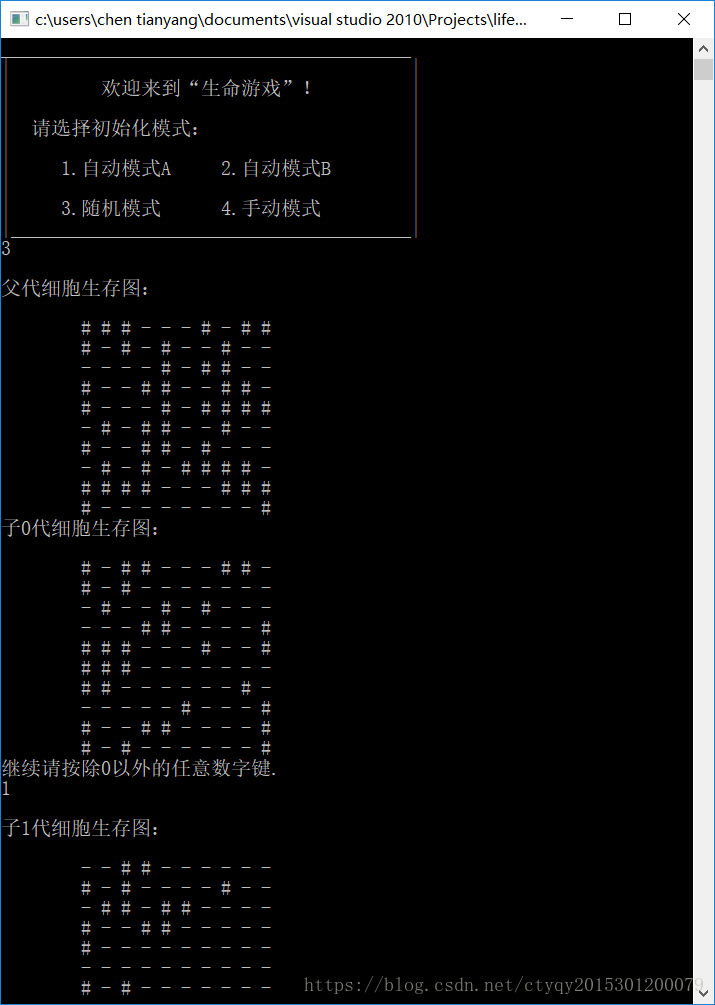
   上图中，“#”表示活细胞，“-”表示死细胞。

   在测试的过程中，可以发现这样一些如下所介绍的稳定结果。

4.1 情形一

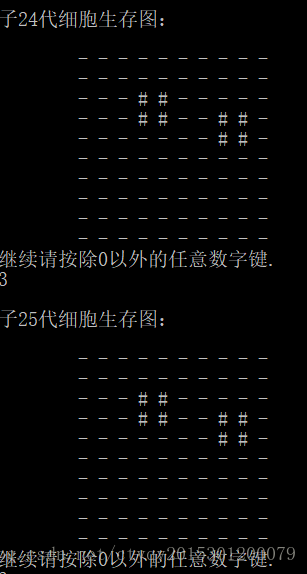
   当父代如图2所示时，子代运行到第24代即可保持稳定，如图3所示。

图2 情形一的父代细胞 图3 情形一的子代细胞至稳定时

4.2 情形二

   当父代如图4所示时，子代运行到第5代即可保持稳定，如图5所示。

图4 情形二的父代细胞 图5 情形二的子代细胞至稳定时

 
   值得注意的是，虽然子5代和子6代细胞的生存图不一致，但是以后所有子代的生存图都是子5代和子6代的循环，因此这也是稳定的。

4.3 情形三

   当细胞数量稍多一些，父代如图6所示时，子代运行到第9代即可保持稳定，如图7所示。

图6 情形三的父代细胞 图7 情形三的子代细胞至稳定时

 
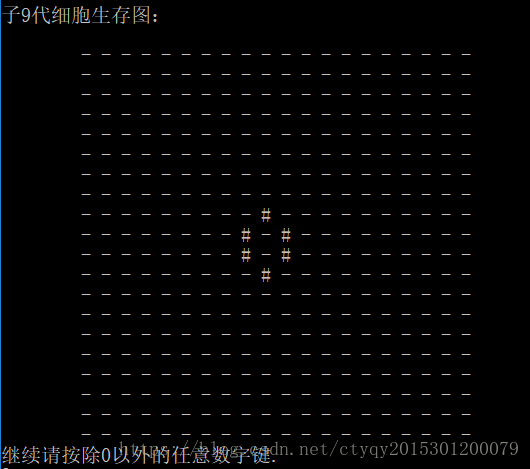
   类似于情形一的“田”字型，这里的6个活细胞构成的空间结构也是稳定的。

4.4 情形四

   最后再尝试一次，父代如图8所示时，子代运行到第77代即可保持稳定，如图9所示。

图8 情形四的父代细胞 图9 情形四的子代细胞至稳定时

 
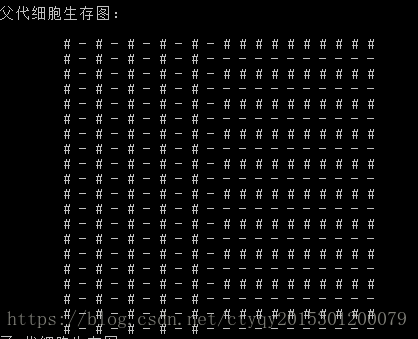
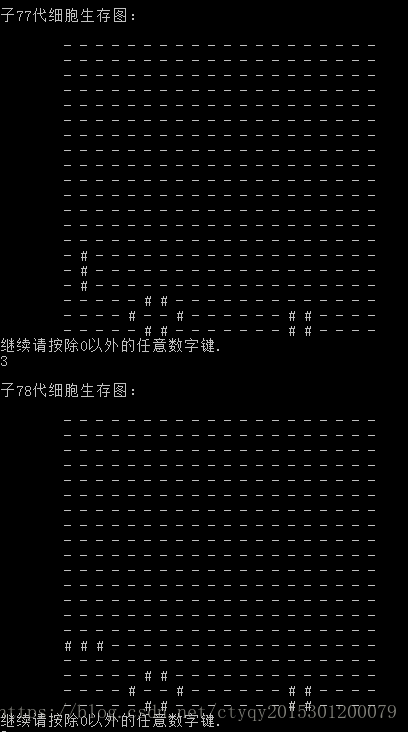
   情形四恰好包含了情形一到情形三的内容，当然也是稳定的。

5 后记

   “生命游戏”虽然是一个零玩家游戏，但却经久不衰。它一直吸引着大量的爱好者的视线，其中包含的乐趣当然不止我所描述的这些。只要上网一查就能找到许多有趣的讨论，比如知乎对生命游戏稳定图形的探讨、果壳网对于计算和宇宙的关系的专访报告以及哔哩哔哩和YouTube上的一些有趣视频等，如果你有兴趣，此话题大有继续探讨的空间和价值。

   转载时务必注明来源及作者。尊重知识产权从我做起。

   代码已上传至网络，欢迎下载，密码是9hrg。