poj 1691 Painting A Board-优快云博客

本文链接：https://blog.youkuaiyun.com/ctxdecs/article/details/24372575

Painting A Board

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3248		Accepted: 1587

Description

The CE digital company has built an Automatic Painting Machine (APM) to paint a flat board fully covered by adjacent non-overlapping rectangles of different sizes each with a predefined color.

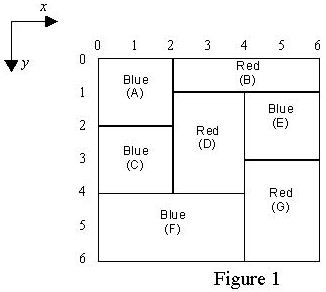
To color the board, the APM has access to a set of brushes. Each brush has a distinct color C. The APM picks one brush with color C and paints all possible rectangles having predefined color C with the following restrictions:
To avoid leaking the paints and mixing colors, a rectangle can only be painted if all rectangles immediately above it have already been painted. For example rectangle labeled F in Figure 1 is painted only after rectangles C and D are painted. Note that each rectangle must be painted at once, i.e. partial painting of one rectangle is not allowed.
You are to write a program for APM to paint a given board so that the number of brush pick-ups is minimum. Notice that if one brush is picked up more than once, all pick-ups are counted.

Input

The first line of the input file contains an integer M which is the number of test cases to solve (1 <= M <= 10). For each test case, the first line contains an integer N, the number of rectangles, followed by N lines describing the rectangles. Each rectangle R is specified by 5 integers in one line: the y and x coordinates of the upper left corner of R, the y and x coordinates of the lower right corner of R, followed by the color-code of R.
Note that:

Color-code is an integer in the range of 1 .. 20.
Upper left corner of the board coordinates is always (0,0).
Coordinates are in the range of 0 .. 99.
N is in the range of 1..15.

Output

One line for each test case showing the minimum number of brush pick-ups.

Sample Input

Sample Output

参考：http://blog.youkuaiyun.com/tsaid/article/details/6841823

dfs

#include <stdio.h>
#include <string.h>

struct Node
{
    int x1, x2, y1, y2; // x1,y1:左上角， x2,y2:右上角
    int clr;
};

Node rc[20];

int up[20][20];	// up[i][0]  矩形i上面有几个矩形 up[i][j] 表示i上面第j个矩形的标号
char vis[20];
int ans, n;

bool check(int i, int j)  // 判断 j是否在i的上面
{
    if (rc[i].y1 != rc[j].y2)
        return false;
    if (rc[i].x1 >= rc[j].x2)
        return false;
    if (rc[i].x2 <= rc[j].x1)
        return false;
    return true;
}

void makeup()
{
    memset(up, 0, sizeof(up));
    for (int i=1; i<=n; ++i)
    {
        for (int j=1; j<=n; ++j)
        {
            if (check(i, j))
            {
                up[i][++up[i][0]] = j;	// 保存i上面的矩形
            }
        }
    }
}


void dfs(int cnt, int clr, int cur) // cnt 染色矩形个数， clr上个矩形染的颜色， cur 表示当前刷的次数
{
    if (cur >= ans)	// 如果刷的次数比以前刷的大
        return;
    if (cnt == n)
    {
        ans = cur;	// 保存结果
        return;
    }

    for (int i=1; i<=n; ++i)
    {
        bool flag = true;
        if (!vis[i])	// i 没有被染色
        {
            for (int j=1; j<=up[i][0]; ++j)	// 检测i上面的矩形是否都被染色
            {
                if (!vis[up[i][j]])
                {
                    flag = false;
                    break;
                }
            }

            if (flag)	// i上面的矩形都被染色
            {
                vis[i] = 1;	// 染色i
                if (rc[i].clr == clr)	// 颜色一样就不加染色次数
                    dfs(cnt+1, clr, cur);
                else
                    dfs(cnt+1, rc[i].clr, cur+1);
                vis[i] = 0;	// 回溯
            }
        }
    }
}

int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d", &n);
        for (int i=1; i<=n; ++i)
        {
            scanf("%d%d%d%d%d", &rc[i].y1, &rc[i].x1, &rc[i].y2, &rc[i].x2, &rc[i].clr);
        }
        
        makeup();
        memset(vis, 0, sizeof(vis));
        ans = 0x7ffffff;
        dfs(0, 0, 0);
        printf("%d\n", ans);
    }
    return 0;

}

状态压缩dp

#include <stdio.h>
#include <string.h>


struct Node
{
    int x1, x2, y1, y2;	// x1,y1:左上角， x2,y2:右上角
    int clr;	
};


Node rc[20];


int up[20];	// up[i]，矩形i上面矩形的染色情况
int dp[1<<16+1][16]; // s表示当前染色的矩形,i最后一个染色的矩形, dp[s][i]表示 当矩形i为最后一个染色时，刷的次数.
int ans, n;


bool check(int i, int j)	// 判断 j是否在i的上面
{
    if (rc[i].y1 != rc[j].y2)
        return false;
    if (rc[i].x1 >= rc[j].x2)
        return false;
    if (rc[i].x2 <= rc[j].x1)
        return false;
    return true;
}


void makeup()
{
    memset(up, 0, sizeof(up));
    for (int i=0; i<n; ++i)
    {
        for (int j=0; j<n; ++j)
        {
            if (check(i, j))
            {
                up[i] |= (1 << j);	// 将i的上面矩形保存
            }
        }
    }
}


void opendp()
{
	memset(dp, 0x7f, sizeof(dp));
	int i, j, k, tmp;
	for (i=0; i<n; ++i)
	{
		if (up[i] == 0)		// i上面没有矩形
			dp[1<<i][i] = 1;	// 要刷1次
	}


	int s, state = (1<<n), news; 


	for (s=0; s<state; ++s)	// 枚举所有的状态
	{
		for (i=0; i<n; ++i)	// 选择i作为最后要刷的矩形 
		{
			if ((1<<i) & s)	// i已经刷过
				continue;
			if ((s & up[i]) != up[i])	// i 上面还有没被刷的。 如 s = 0110,（当前染色3，2） up[i] = 1110, 表明i上面有4，3，2，的矩形要染色
				continue;
			for (j=0; j<n; ++j) // 选择j作为最后要刷的矩形 
			{
				if ((s & (1<<j)) == 0)	// 判断j是否被染色
					continue;
				news = (s | (1<<i));	// i染色
				tmp = dp[s][j];
				// 比较i和j分别作为最后矩形，谁的染的次数少
				// 因为i和j最后的s是一样的
				if (rc[i].clr != rc[j].clr)
					tmp++;	
				if (tmp < dp[news][i])	// 选择最小的
					dp[news][i] = tmp;
			}
		}
	}


	for (i=0; i<n; ++i)
	{
		if (ans > dp[state-1][i])
			ans = dp[state-1][i];
	}
}


int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d", &n);
        for (int i=0; i<n; ++i)
        {
            scanf("%d%d%d%d%d", &rc[i].y1, &rc[i].x1, &rc[i].y2, &rc[i].x2, &rc[i].clr);
        }
        
        makeup();	// 建立


        ans = 0x7ffffff;
        opendp();
        printf("%d\n", ans);
    }
    return 0;


}