帅到没朋友算法解析-优快云博客

本文解析了三个经典算法问题：找出帅到没朋友的人、判断小顶堆的相关命题及链表去重，并提供了详细的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

帅到没朋友

当芸芸众生忙着在朋友圈中发照片的时候，总有一些人因为太帅而没有朋友。本题就要求你找出那些帅到没有朋友的人。

输入格式：
输入第一行给出一个正整数N（≤100），是已知朋友圈的个数；随后N行，每行首先给出一个正整数K（≤1000），为朋友圈中的人数，然后列出一个朋友圈内的所有人——为方便起见，每人对应一个ID号，为5位数字（从00000到99999），ID间以空格分隔；之后给出一个正整数M（≤10000），为待查询的人数；随后一行中列出M个待查询的ID，以空格分隔。

注意：没有朋友的人可以是根本没安装“朋友圈”，也可以是只有自己一个人在朋友圈的人。虽然有个别自恋狂会自己把自己反复加进朋友圈，但题目保证所有K超过1的朋友圈里都至少有2个不同的人。

输出格式：
按输入的顺序输出那些帅到没朋友的人。ID间用1个空格分隔，行的首尾不得有多余空格。如果没有人太帅，则输出No one is handsome。

注意：同一个人可以被查询多次，但只输出一次。

输入样例1：

3
3 11111 22222 55555
2 33333 44444
4 55555 66666 99999 77777
8
55555 44444 10000 88888 22222 11111 23333 88888

输出样例1：

10000 88888 23333

输入样例2：

3
3 11111 22222 55555
2 33333 44444
4 55555 66666 99999 77777
4
55555 44444 22222 11111

输出样例2：

No one is handsome

#include <stdio.h>
int main()
{
	int a[100000]={ 0 };
	int N,K,M; 
	int i,n,m,sum=0;
	scanf("%d",&N); 
	while(N--)
	{
		scanf("%d",&K);
		for(i=1;i<=K;i++)
		{
			scanf("%d",&n);
			if(K!=1)//但题目保证所有K超过1的朋友圈里都至少有2个不同的人,这个地方我没有看到
			{
				a[n]+=K;//a[n]=1;
			}	 
		}
	}
	scanf("%d",&M);	
	while(M--)
	{
		scanf("%d",&m);
		if(a[m]==0)
		{
			if(sum!=0) printf(" ");
			printf("%05d",m);
			a[m]=1;
			sum++; 
		}		
	}
	if(sum==0) printf("No one is handsome");
	return 0;
}

关于堆的判断 (25 分)

将一系列给定数字顺序插入一个初始为空的小顶堆H[]。随后判断一系列相关命题是否为真。命题分下列几种：

x is the root：x是根结点；
x and y are siblings：x和y是兄弟结点；
x is the parent of y：x是y的父结点；
x is a child of y：x是y的一个子结点。

输入格式：
每组测试第1行包含2个正整数N（≤ 1000）和M（≤ 20），分别是插入元素的个数、以及需要判断的命题数。下一行给出区间[−10000,10000]内的N个要被插入一个初始为空的小顶堆的整数。之后M行，每行给出一个命题。题目保证命题中的结点键值都是存在的。

输出格式：
对输入的每个命题，如果其为真，则在一行中输出T，否则输出F。

输入样例：

5 4
46 23 26 24 10
24 is the root
26 and 23 are siblings
46 is the parent of 23
23 is a child of 10

输出样例：

F
T
F
T

#include <iostream>
#include <cstdio>
#include <cstring>
#include <climits>
#include <vector>
#include <queue>
#include <map>
#include <string>
#include <algorithm>
using namespace std;
const int N = 1e4+10;
const int inf = 99999999;
int a[N], cnt;
void build(int x)//堆
{
    a[++cnt]=x;//新加点x
    int t=cnt;//t表示新加的结点放在哪个位置
    while(t>1&&(a[t/2]>a[t]))//判断是否需要上移
    {
        swap(a[t/2],a[t]);//交换
        t/=2;//继续往上交换
    }
    return ;
}
map<int,int>q;
int main()
{
    int n, m, x, y;
    scanf("%d %d", &n, &m);
    cnt=0;
    for(int i=1; i<=n; i++)
    {
        scanf("%d", &x);
        build(x);
    }
    for(int i=1; i<=n; i++) q[a[i]]=i;//层序
    string s;
    for(int i=0; i<m; i++)
    {
        cin>>x;
        cin>>s;
        if(s[0]=='a')
        {
            cin>>y;
            getline(cin,s);//可以读空格
            if(q[x]/2==q[y]/2) puts("T");//sings
            else puts("F");
        }
        else
        {
            cin>>s;
            cin>>s;
            if(s[0]=='r')//root
            {
                if(q[x]==1) puts("T");
                else puts("F");
            }
            else if(s[0]=='p')//father
            {
                cin>>s;
                cin>>y;
                if(q[x]==q[y]/2) puts("T");
                else puts("F");
            }
            else//son
            {
                cin>>s;
                cin>>y;
                if(q[x]/2==q[y]) puts("T");
                else puts("F");
            }
        }
    }
    return 0;
}

链表去重 (25 分)

给定一个带整数键值的链表 L，你需要把其中绝对值重复的键值结点删掉。即对每个键值 K，只有第一个绝对值等于 K 的结点被保留。同时，所有被删除的结点须被保存在另一个链表上。例如给定 L 为 21→-15→-15→-7→15，你需要输出去重后的链表 21→-15→-7，还有被删除的链表 -15→15。

输入格式：
输入在第一行给出 L 的第一个结点的地址和一个正整数 N（≤10
5
，为结点总数）。一个结点的地址是非负的 5 位整数，空地址 NULL 用 -1 来表示。

随后 N 行，每行按以下格式描述一个结点：

地址键值下一个结点
其中地址是该结点的地址，键值是绝对值不超过10
4
的整数，下一个结点是下个结点的地址。

输出格式：
首先输出去重后的链表，然后输出被删除的链表。每个结点占一行，按输入的格式输出。

输入样例：

00100 5
99999 -7 87654
23854 -15 00000
87654 15 -1
00000 -15 99999
00100 21 23854

输出样例：

00100 21 23854
23854 -15 99999
99999 -7 -1
00000 -15 87654
87654 15 -1

#include<bits/stdc++.h>
using namespace std;

struct node{
	int key;
	int next;
}; 
struct node L[100000];
bool flag[100000];//标志数组 
int newL[100000],del[100000];//存放地址 
int main()
{
	int first,N,addr;
	cin>>first>>N;
	for(int i=0;i<N;i++)//输入 
	{
		cin>>addr;
		cin>>L[addr].key>>L[addr].next;
	}
	memset(flag,true,sizeof(flag));//对flag[100000]全部赋值1
	int num1=0,num2=0;
	for(int i=first;i!=-1;)
	{
		int k=abs(L[i].key);
		if(flag[k])//K是第一个键值 
		{
			flag[k]=false;
			newL[num1++]=i;//把地址存进newL里面，新链表的地址 
		}
		else del[num2++]=i;
		i=L[i].next;//下一个结点，i作为数组下标 
	}
	printf("%05d %d ",newL[0],L[newL[0]].key);
	for(int i=1;i<num1;i++)
	{
		printf("%05d\n",newL[i]);//输出当前结点的地址，同时也是上一结点的next 
		printf("%05d %d ",newL[i],L[newL[i]].key);//输出地址和键值 
	}
	printf("-1\n");//新链表结束 
	if(num2)//删掉的链表不空
	{
		printf("%05d %d ",del[0],L[del[0]].key);
		for(int i=1;i<num2;i++)
		{
			printf("%05d\n",del[i]);//输出下一个节点的地址 
			printf("%05d %d ",del[i],L[del[i]].key);//输出地址和键值 
		}
		printf("-1\n");
	} 
	return 0;
}

玩转二叉树 (25 分)

给定一棵二叉树的中序遍历和前序遍历，请你先将树做个镜面反转，再输出反转后的层序遍历的序列。所谓镜面反转，是指将所有非叶结点的左右孩子对换。这里假设键值都是互不相等的正整数。

输入格式：
输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其中序遍历序列。第三行给出其前序遍历序列。数字间以空格分隔。

输出格式：
在一行中输出该树反转后的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
1 2 3 4 5 6 7
4 1 3 2 6 5 7

输出样例：

4 6 1 7 5 3 2

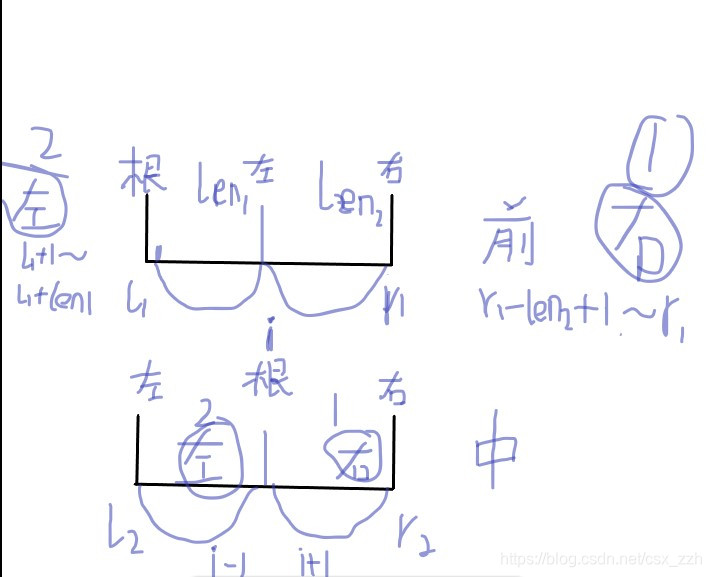
在这里插入图片描述

#include <iostream>
#include<cstring>
#include<stdio.h>
using namespace std;
int post[35],in[35],pre[35],level[35];
int N=0;
//l1~r1前序的区间，l2~r2中序的区间
/*
所谓的层次遍历的序列就是要按照从上到下从左到右的顺序输出来。
但这里眼球镜面反转后在输出层次遍历的序列，
我们一般在根据前序和中序确定一棵树的时候，先递归这棵树的左子树再递归右子树，
但如果我们现在先递归右子树再递归左子树，这样每次递归的根节点的出现序列就是镜面反转后的序列。
*/

void postTranverse(int l1,int r1,int l2,int r2,int id)
{
    if(l1>r1||l2>r2) return;
    int i,len1,len2;
    for(i=l2; i<=r2; i++)
    {
        if(pre[l1]==in[i])//从中序中找到当前的根节点
        {
            level[N]=id;
            post[N++]=in[i];
            len1=i-l2;//左子树的长度
            len2=r2-i;//右子树的长度
            break;
        }
    }
    postTranverse(r1-len2+1,r1,i+1,r2,id+1);//递归右子树
    postTranverse(l1+1,l1+len1,l2,i-1,id+1);//递归左子树
}
int main()
{
    int n,i,j;
    cin>>n;
    for(i=0; i<n; i++)
    {
        scanf("%d",&in[i]);//中序遍历序列
    }
    for(i=0; i<n; i++)
    {
        scanf("%d",&pre[i]);//前序遍历序列
    }
    memset(level,-1,sizeof(level));
    postTranverse(0,n-1,0,n-1,0);
    int t=1;
    printf("%d",post[0]);
    for(i=1; i<n; i++)
    {
        for(j=1; j<n; j++)
        {
            if(level[j]==t)
            {
                printf(" %d",post[j]);
            }
        }
        ++t;
    }
    return 0;
}

凑零钱 (30 分)

在这里插入图片描述
简单dfs();

#include <bits/stdc++.h>
using namespace std;
const int maxn=100050;
int n,m;
int sum=0;
int a[maxn];
int ans[maxn];
int f=0;
int cnt=0;
void dfs(int x,int step)
{
	if(step>m) return ;
	if(step==m)
	{
		f=1;
		for(int i=0; i<cnt; i++)
			printf(i==cnt-1?"%d":"%d ",ans[i]);
        printf("\n");
		return;
	}
	else
	{
		for(int i=x; i<n; i++)
		{
			ans[cnt++]=a[i];
			dfs(i+1,step+a[i]);
			if(f) break;
			cnt--;
		}
	}
}
int main()
{
	cin>>n>>m;
	for(int i=0; i<n; i++)
	{
		cin>>a[i];
		sum+=a[i];
	}
	if(sum<m)
	{
		printf("No Solution");
	}
	else
	{
		sort(a,a+n);
		dfs(0,0);
		if(f==0)
		{
			printf("No Solution");
		}
	}
}