保卫国王大道

 通过向量创建图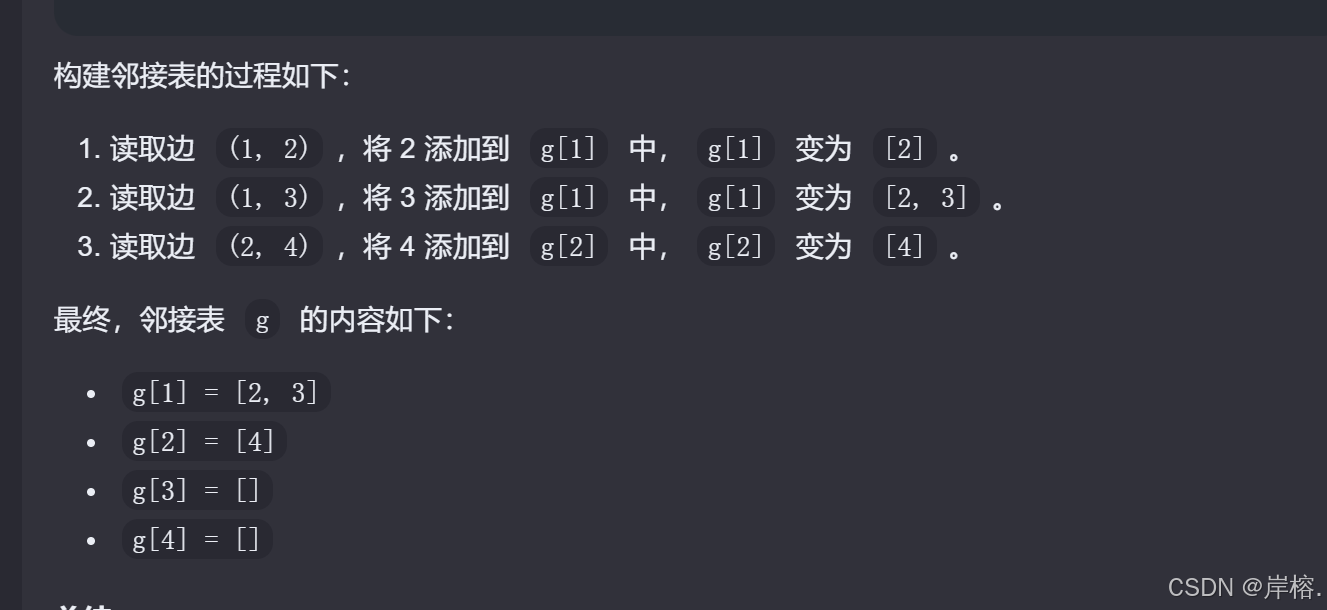

向量：

邻接图的创建
vecotr能够在一个位置插入多个元素
不只是能够动态扩展长度


数组：

数组只能够在同一位置插入一个元素，并且长度固定。

---

树状DP 求最小顶点覆盖

即每一条边至少又一个顶点被选择

    1
   / \
  2   3
 / \
4   5

节点 1：
子节点：2, 3
dp[1][0]：不选择节点 1 作为军营，子节点 2 和 3 必须选择作为军营。
dp[1][1]：选择节点 1 作为军营，子节点 2 和 3 可以选择也可以不选择作为军营。
节点 2：
子节点：4, 5
dp[2][0]：不选择节点 2 作为军营，子节点 4 和 5 必须选择作为军营。
dp[2][1]：选择节点 2 作为军营，子节点 4 和 5 可以选择也可以不选择作为军营。
节点 3：
没有子节点
dp[3][0]：不选择节点 3 作为军营，无法覆盖与 3 相连的边，因此 dp[3][0] = ∞。
dp[3][1]：选择节点 3 作为军营，dp[3][1] = 1。

//最小顶点覆盖
//最小顶点覆盖问题就是每一条边至少有一个端点被选择
#include<bits/stdc++.h>
using namespace std;
const int N=3e5;  //定义最大节点数
int dp[N][3];     //dp数组，dp[i][0]表示不选择节点i作为军营时，覆盖所有边的最小军营数量；dp[i][1]表示选择节点i作为军营时，覆盖所有边的最小军营数量
vector<int> g[N]; //邻接表，存储图的结构

//深度优先搜索函数，用于求解最小顶点覆盖
void dfs(int x){
    if(!x)return; //设置出口，防止访问空节点，当然不设置也可以，因为题目保证了输入的图是合法的
    //遍历节点x的所有子节点
    for(const auto &q:g[x]){
        dfs(q); //递归求解子节点的最小顶点覆盖
        dp[x][0]+=dp[q][1]; //不选择节点x作为军营，则子节点必须选择作为军营，才能覆盖与x相连的边
        dp[x][1]+=min(dp[q][1],dp[q][0]); //选择节点x作为军营，则子节点可以选择作为军营，也可以不选择，取两者中的最小值
        //当前节点设置军营，则子节点是否设置都行，取最小的即可
    }
    dp[x][1]+=1;
    //返回的时候确定将当前的节点设置军营所以要+1
    //上面的for循环只是考虑了父节点的子节点，
    //综合考虑完之后要加上自己的“影响”然后传递给下一个
}

int main(){
    int n;cin>>n; //输入节点数
    for(int i=1;i<n;i++){ //读取图的边
        int x,y;cin>>x>>y;
        g[x].push_back(y); //构建邻接表
    }
    dfs(1); //从节点1开始深度优先搜索
    cout<<min(dp[1][0],dp[1][1]); //输出最优结果，即不选择节点1作为军营和选择节点1作为军营两种情况下的最小值
    return 0;
}