基于生理信号的快速诱饵点生成算法

基于生理信号的快速无效点（RPSC）生成算法 在体域网系统中通过树莓派实现MATLAB仿真 与患者生理信号通信

摘要

无线体域网（WBAN）在植入式心脏复律除颤器 （ICDs）、神经刺激器等医疗领域中具有重要意义。植 入式医疗设备（IMDs）内的体域网信息必须确保安全， 其隐私也必须得到保护。若接口缺乏防护，攻击者将容 易获取对IMD的控制权。因此，在密钥协商方案中，对 无线接口的保护已成为IMD中的必要措施。为保障密钥 协商方案的安全性，目前最实用且轻量化的生物密码系 统——模糊保险箱（FV）被广泛采用。在FV方案中，计 算最密集的任务是诱饵点生成过程，用于将密钥K和有效 点隐藏在保险库中。为此，本文提出了一种基于树莓派 实现的MATLAB仿真与生理信号通信的快速干扰点生成 （RPSC）算法，应用于WBAN。RPSC算法减少了干扰 点生成过程中候选干扰点的数量，从而降低了整体执行 时间。该RPSC算法的时间复杂度为O(n2)，相较于现有 的O(n3)复杂度有显著改进。在0.7秒的较短计算时间内生 成504个诱饵点时，RPSC算法相比克莱恩算法加速性能 提升206倍，比哈利尔算法快130倍，比阮氏算法快93倍。
实验中采用树莓派3代专业版（RPi3）硬件模块作为植入 式医疗设备和编程设备，用于实现干扰点生成以及所提 WBAN的实时通信模块。

关键词

认证；诱饵点；设计；模糊保险箱；植入式医 疗设备

引言

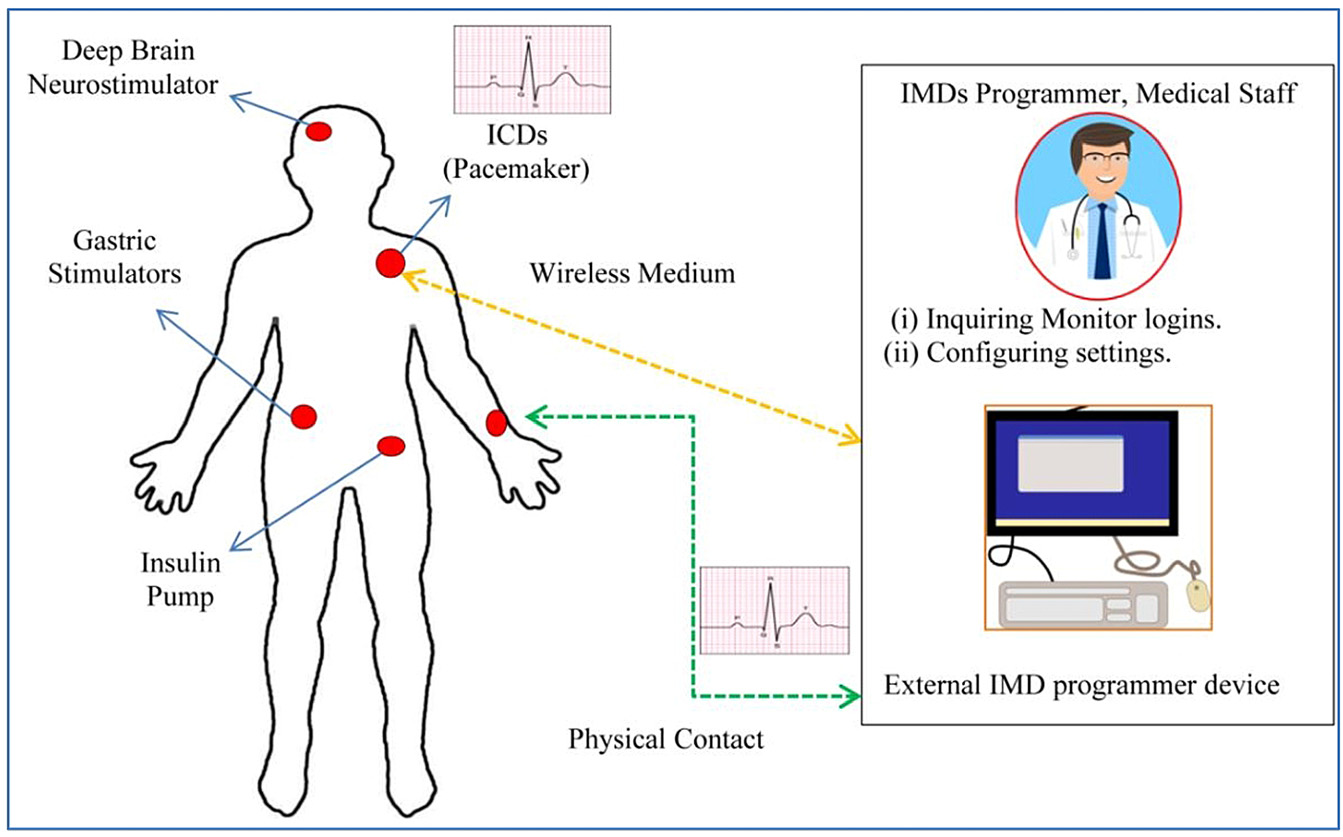
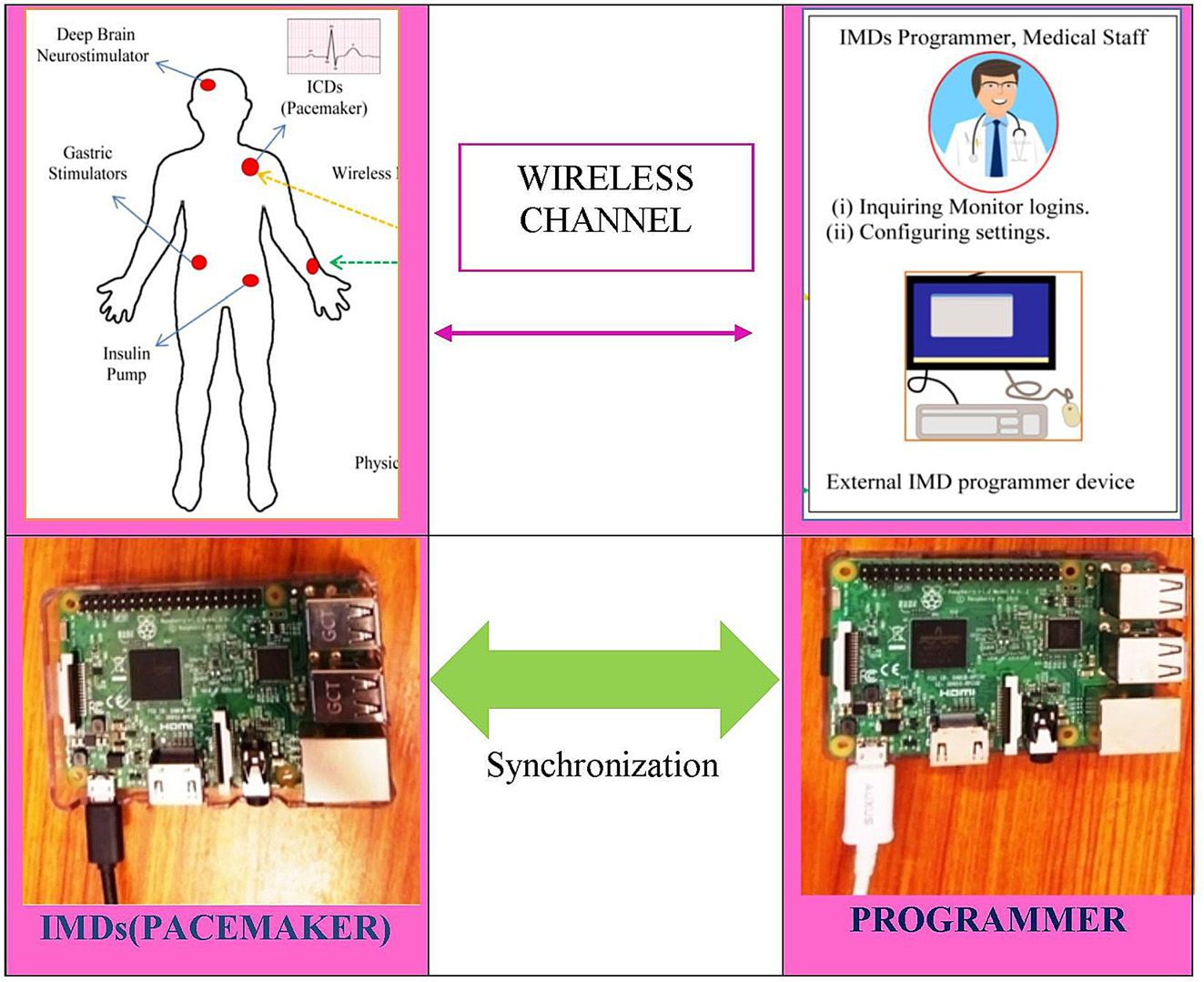
植入式医疗设备（IMDs）由无线模块、小型处理器和微型电池[1]组成。因此，必须设计一种轻量级操作系统， 并结合轻量级安全算法（LW security algorithm）， 以保护数据和设备免受攻击者侵害。植入人体内的I MD通过无线遥测接口连接到另一个可靠节点或IMD编 程器。设备之间的无线通信并非认证通道，传输的信息 也是未加密的[2]。无线模块仅具备简单的密码保护，一旦被破解，就可能对软件协议（该协议本用于挽救生命） 进行无线重新配置，或篡改传输信号。生理信号（PS） 包含重要信息，若在通信过程中遭到窃取，可能导致错误治疗，进而引发危及生命的情况。本研究聚焦于一级 无线体域网（WBAN）设备的安全性，因为有必要针对 其中出现的各种威胁提出令人满意的解决方案。工作场 景如图1所示，包含IMD与外部IMD编程器。本文开发了 一种轻量级安全方案，基于树莓派实现MATLAB仿真， 并采用基于生理信号快速生成诱饵点的通信方法（ RPSC），以实现设备间的数据隐私保护和设备认证。
所提出的RPSC系统包含两个部分——通常称为 IMD的植入式心脏复律除颤器（ICDs）和外部编程器[3]。
ICD是一种医疗设备，植入患者体内以持续监测患者的 心电信号（ECG信号）。此后，ICD或任何其他可重构 设备均表示为IMD。放置在患者手腕上的外部心电传感 器连接到编程器，并测量心电信号。IMDs是需要建立的手术植入系统
通过无线通信与外部编程器连接，以访问植入式医疗设 备配置。医生使用外部编程设备进行通信并诊断问题[4]。
在某些情况下，当需要更改植入式医疗设备的设置时， 可通过连接编程设备重新配置植入式医疗设备，使其根 据患者当前的医疗状况运行；所有这些操作都将通过植 入式医疗设备的无线模块完成。
可重新配置的植入式医疗设备是最流行的一种类型， 因为一旦将这些设备植入人体内，就可以根据情况通过 无线遥测接口从外部对其进行重新配置。这种重新配置 通过编程设备安全地完成，无需进行任何手术程序。因此患者更倾向于使用可重新配置的植入式医疗设备，本文提出的工作也采用了这类植入式医疗设备。当使用专用频段（如医用植入通信服务（MICS））时，无线通信 链路之间传输的通信信息是未加密的，且共享网络的设备也未经认证。因此，在无线体域网中采用轻量级安全 性算法来保障植入式医疗设备与编程设备之间的无线通 信安全性已成为必要要求[5]。
在最近的实验研究中，一些攻击表明患者的安全性 已受到威胁，例如数据隐私和设备认证。[6] 实施的实际攻击设计了一种定制的软件定义无线电（SDR），用于监听体域节点（BN）与体域网协调器（BNC）之间无线信道中的未加密数据。该设备被编程为在不干扰通信频率的情况下，静默地监听、捕获并解码数据通信（窃听）。
学习了用于控制无线体域网设备的数据和命令指令。
哈尔佩林等人[7]的另一项实际演示表明，通过逆向 工程追踪设备之间开放无线信道上的通信，获取了命令 指令，并实现了对胰岛素泵的控制。此类主动攻击加剧 了建立数据隐私和设备认证安全模型的难度。这类攻击 可能将患者的医疗状况泄露给未授权的编程器，并导致 重放攻击或注入攻击，造成严重后果。在重放攻击的情 况下，植入式医疗设备电池也可能被不必要地耗尽。窃 听、新鲜性检查、重放攻击和注入攻击都可能发生在通 信链路上，并攻击植入式医疗设备的无线模块[8]。而通 信链路攻击可能导致拒绝服务（DoS）攻击，使预期用 户无法正常接入。
因此，需要一种更实用的硬件模型来保护网络中的 无线体域网数据和设备。本文提出并实现了一种更合适的生物特征轻量级安全模型。采用了不同的密钥协商和 认证方法，以避免在传输过程中造成数据隐私泄露以及 实现无线体域网内设备的认证。这推动了RPSC算法的发展，以减少干扰点的计算时间，并提高系统整体效率， 增强无线体域网中的数据隐私和设备认证。然而，所提 出的干扰点生成方案非常少，且由于其计算任务繁重， 导致这些模型在片上系统（SOC）实现中具有不适用性。
[9]。直接致力于实现诱饵点生成、密钥协商以及实时证 明设备认证的硬件实现部分。使用两个树莓派3模块创建 了两个设备之间通信的真实场景。实现了诱饵点生成的 实用硬件方案，以及通过无线通信将密钥从植入式医疗 设备传输到树莓派3上的编程器。

文献综述

Venkatasubramanian 等人[10]利用频域分析从患者光 电容积描记法（PPG）信号中进行密钥生成。通过模糊 保险箱（FV）方案，数据在节点之间安全共享。从 PPG信号中提取特征的侵入式传感器生成有效点。随后， 将密钥值作为系数用于构造 νth阶多项式方程（PE）， 并与有效点结合。该结合值称为特征向量（FV）。然而， 系统在传输过程中的安全性仍然脆弱，容易受到攻击。
为了提高系统安全性，生成干扰（虚拟）点并将其与 FV结合。为解锁模糊保险箱，接收端也会利用人体指尖 或耳部检测到的PPG信号生成一组类似的 有效点。在接收设备上，首先去除干扰点，然后从PPG信号中生成有效点。之后解锁保险库，并从多项式方程中提取随机密钥。这验证了发送设备的真实性。若无共同的PPG特征 有效点，则无法解锁保险库。但该方法仍存在缺陷，即 需要生成1000个随机生成的干扰点。这种诱饵点生成是 一个计算密集型过程，耗时且消耗额外电池电量。在此， 作者并未详细讨论诱饵点生成方法。
作者Venkatasubramanian 等人提出了一种基于生 理信号的密钥协商（PSKA）方案，该方案非常高效地利 用了受试者的生理信号（如心电图/光电容积描记），因 为这些信号具有唯一性和随机性，且无法再生[11]。他从 患者的ECG/PPG信号中提取特征点，对生理信号（PS） 应用快速傅里叶变换（FFT），生成一组有效点。基于 伪随机数生成（PRNG）的方式生成一个密钥K，并将其 转换为多项式PE的系数。接着，将多项式和有效点结合 以构建特征向量（FV）。由于多项式点容易被识别和分 离，因此在保险库中添加大量干扰点以增强安全性。
重叠密钥K和有效点。密钥被安全地锁定在保险库中，并 与干扰点一起存储，密钥在节点之间通信时以安全性的 方式共享，且无需相同的有效点集合即可解锁。然而， 该方法仍存在应用复杂随机诱饵点生成的缺点。
作者苗芬等人提出了一种密钥协商方案[12]。利用患 者的生理信号（PS）生成随机比特，并基于这些比特构 建密钥K。多项式次数从6增加到20，同时在不同级别上 观察FV安全模型。实验结果表明，随着多项式阶数逐步 增加，半容忍错误率（HTER）显著降低了10倍，且误 接受率（FAR）和误拒率（FRR）的数值表现良好。该 方案中生成了额外的混淆诱饵点以提高安全性。干扰点 通过随机数生成方法产生，这是一种复杂的算法，增加 了发射器和接收端的整体计算量。然而，该密钥协商方 案未讨论诱饵点生成阶段。
崔元硕等人提出了一种高效节能（E2PKA）模型， 该模型降低了整体计算能耗[13]。该研究声称是一种在两 个传感器之间实现的、能耗较低的密钥协商方案。在此 工作中，密钥和密钥协商方案基于患者的生理值（PV）。
密钥是根据两个传感器共同测量到的患者最高频成分生 成的。该工作将能耗从20.23 mV降低至7.024 mV。然而，该研究并未提出任何强健的密钥协商方案，且存在 一个主要缺陷，即假阴性率（FNR）较高，相较于以往 的安全模型失败率更高。
首个提出的诱饵点生成思想基于朱尔等人的研究。
在此提出的模型中，一个随机点被预先分布在XY平面上， 并检查其是否满足FV方案的满意操作。作者[14]在构建 干扰点时制定了一套基本规则。首先，生成的诱饵点不 能过于靠近或与从心电信号提取的有效点重叠，且应与 其保持最小距离；其次，它也不应位于已生成的多项式 系数上。在此方法中，会在有效的XY区域内创建多个随 机点。所生成的随机点在植入式医疗设备内的内存空间 消耗较少。该诱饵点方法并未包含测量有效点与诱饵点 之间距离的技术，因此后续的诱饵点生成算法提出了新 的距离计算方法。

在克莱西等人提出的方法[15], 中，随机点在 XY 平面内围绕有效点生成，并设定距离“δ”（δ>10.7）。计算各点之间的欧几里得距离，并以从有效点出发的距离 D 构建矩阵。若新点与先前各点之间的距离大于或等于 值“δ”，则将该新随机点作为诱饵点交替添加到特征向 量中；若某点距离过短或过于接近其他点，则将其舍弃 并重新开始搜索新的诱饵点。此方法的主要缺点在于， 欧几里得距离的计算总数多于实际添加的干扰点总数。
因为在执行过程中间或末尾生成的一些生成的诱饵点可 能会与其他已存在的点重叠或靠得太近，从而需要被丢弃。因此，欧几里得距离计算所涉及的干扰点数量多于 实际添加的干扰点，导致需要大量诸如平方和平方根的 计算操作。随着干扰点数量的增加，计算量呈现线性增 长。
在乌卢达格等人中，作者提出了[16]一种关于特征 向量和诱饵点生成系统的扩展工作。该方法在XY平面上 与其他点保持 δ=25的最大距离。因此，通过增加有效点 与诱饵点之间的距离，减少了多余的计算。这样，诱饵 点不会与其他诱饵点过于接近，因为其距离是原来的两 倍。这项工作消除了诱饵点近距离共存的问题。这使得 系统更加安全，攻击者更难解码密钥。这项工作的缺点 是，当诱饵点彼此相距很远时，诱饵点生成的算法复杂度为O(n3)。这种较大的距离本身反而证明了诱饵点的可 识别性。此外，在生成和存储过程中，较大的距离占用 了更多的内存空间。
哈利德等人[17]提出了一种针对特征向量的动态且 高效的诱饵点生成方案。他们通过采用圆周停放法，降 低了关键且密集的诱呗点生成需求。在第一步中，对每 个有效点绘制一个距离为“δ”的圆。初始时，作者设定 从有效点出发的边界距离大于“δ”。当需要添加新的诱 饵点时，该点必须大于边界距离（δ/2），以避免与现有 点重叠。诱饵点生成分为多个阶段进行。首先，生成两 个经验距离，即较小的距离 ds 和较大的距离 dl，用于在 生成范围内产生最大数量的干扰点。在下一阶段，从特 征向量中选择一个有效点，并在该有效点的右、左、上、 下四个方向上利用生成的值形成四个边界点。这些点在X‐Y方向上的距离从上述范围内随机选取。
然后为其中一个点创建四个边界点。如果新形成的边界 点不在FV中任何其他成员的边界内，则该点被添加为 FV中的一个诱饵点，否则丢弃新生成的点。此过程对剩 余的三个点重复执行。每个有效点周围的边界由一个边 界矩阵指定。当向FV中添加新的有效点时，边界矩阵会 更新。其优点是保险库中生成的所有点彼此之间都保持 最小距离，且所使用的计算任务仅涉及加减逻辑。整体 复杂度从克莱西的复杂度时间O(n3)降低到O(n2)。该方 法的缺点是当存在大量诱饵点时，候选诱饵点的复杂度 和执行时间增加。为了降低计算复杂度，作者在生成诱 饵点时采用了加法和减法，而不是平方和平方根运算。
阮氏行等人提出了一种快速干扰点生成算法[18]。采 集指纹图像并假设其为一个正方形。该算法在指纹图像 中随机选择一个像素作为候选诱饵点。如果该候选诱饵 点是任意图像单元中唯一的点，并且该点与最近的八个 现有关键点之间的欧几里得距离为 ≥δ(距离)，则该候选 诱饵点可成为有效的诱饵点。由于约束条件较低，干扰 点的绘制得以更快且高效地完成。使用该算法可以减少 计算时间，且计算复杂度低于O(n2)。唯一的缺点是它需 要3276次迭代，并且每幅图像都被视为正方形。该研究 未充分讨论特征向量，也没有进行实际实现。
甘迪马蒂等人提出的方案应用了仿生粒子群优化 （PSO）搜索算法。选择PSO用于生成诱饵点，因其需 调整的参数较少，能有效避免收敛于局部最小值，并可 通过随机搜索快速启动[19]。该研究作者采用优化技术， 从人脸和耳朵特征提取点中定位最佳特征向量以识别干 扰点，其中位置的选择是通过PSO算法的优化技术完成 的。在此过程中，首先将特征提取点转换为位置，并在 该候选点周围生成干扰点。从每个位置获得最佳适应度 值，其中最优匹配被标记为全局最优解“gbest”。通过 迭代找到最佳位置，并将其转换为

有效点的面部或耳部点的诱饵点。它存在从一个点到另 一个点收敛速度慢且耗时的缺点。由于数学复杂性，步 长过小，表现出性能有限。在接近最大值后，会因随机 性不足而受到影响，达到最大峰值后参数调优变得困难。
这种两阶段PSO在实现上具有较高的复杂性。

模糊保险箱方案

提出了一种用于密钥协商系统的RPSC算法。本节介绍了 特征向量锁定和解锁过程。

模糊保险箱锁定阶段

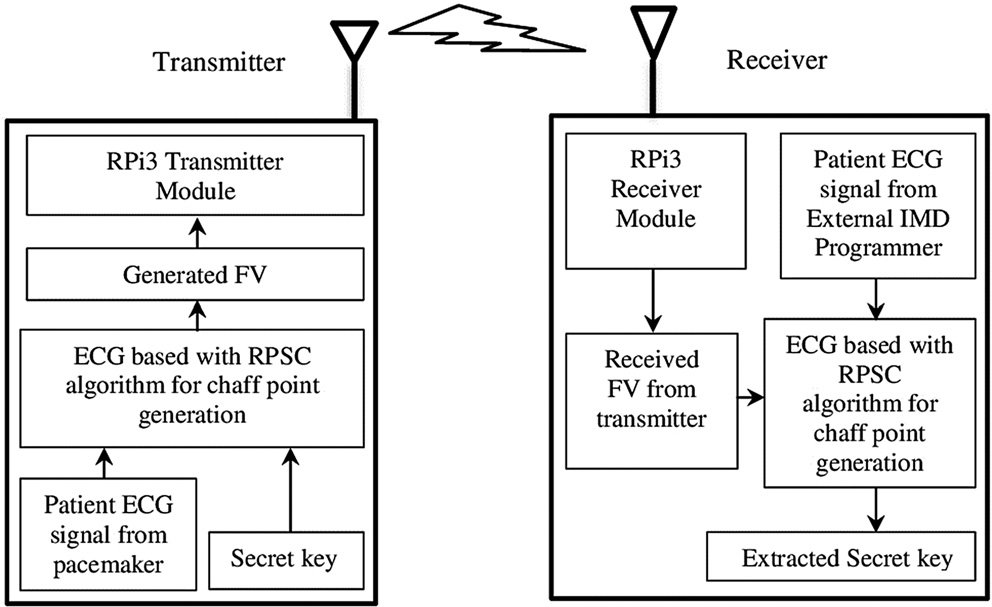
RPSC实现了密钥从植入式医疗设备（IMDs）到编程器 的安全传输，并实现这些设备之间的设备认证。锁定过 程在多个阶段进行；首先，在植入式医疗设备中生成密 钥，并用于生成PE系数。接下来，从患者获取心电信号， 并进行特征提取以形成一组有效点。将PE和有效点结合 形成特征向量（FV），再结合诱饵点完成特征向量锁定 （FV locking）过程。整个特征向量锁定过程可数学表 达如下。在特征向量锁定过程中，密钥K是由较长随机字 符串组成的行矩阵，其表示为
K=[Kg−1Kg−2 ......K1] (1)
密钥K与其校验和连接，形成一个新的维度加密密钥k′， 如公式(2)所示。G是执行密钥K的校验和操作′并将校验 和与密钥K连接以得到K值的参数。
K′= Ĝ(K)=[K cs(K)] (2)
每个ki Є K是ith系数，用于构造一个多项式Q(x)， 该多项式的次数为(g‐1)，其表达式由以下给出
Q(x)=(Kg − 1 Xg − 1+ K g − 2 Xg − 2+…K0 ) (3)
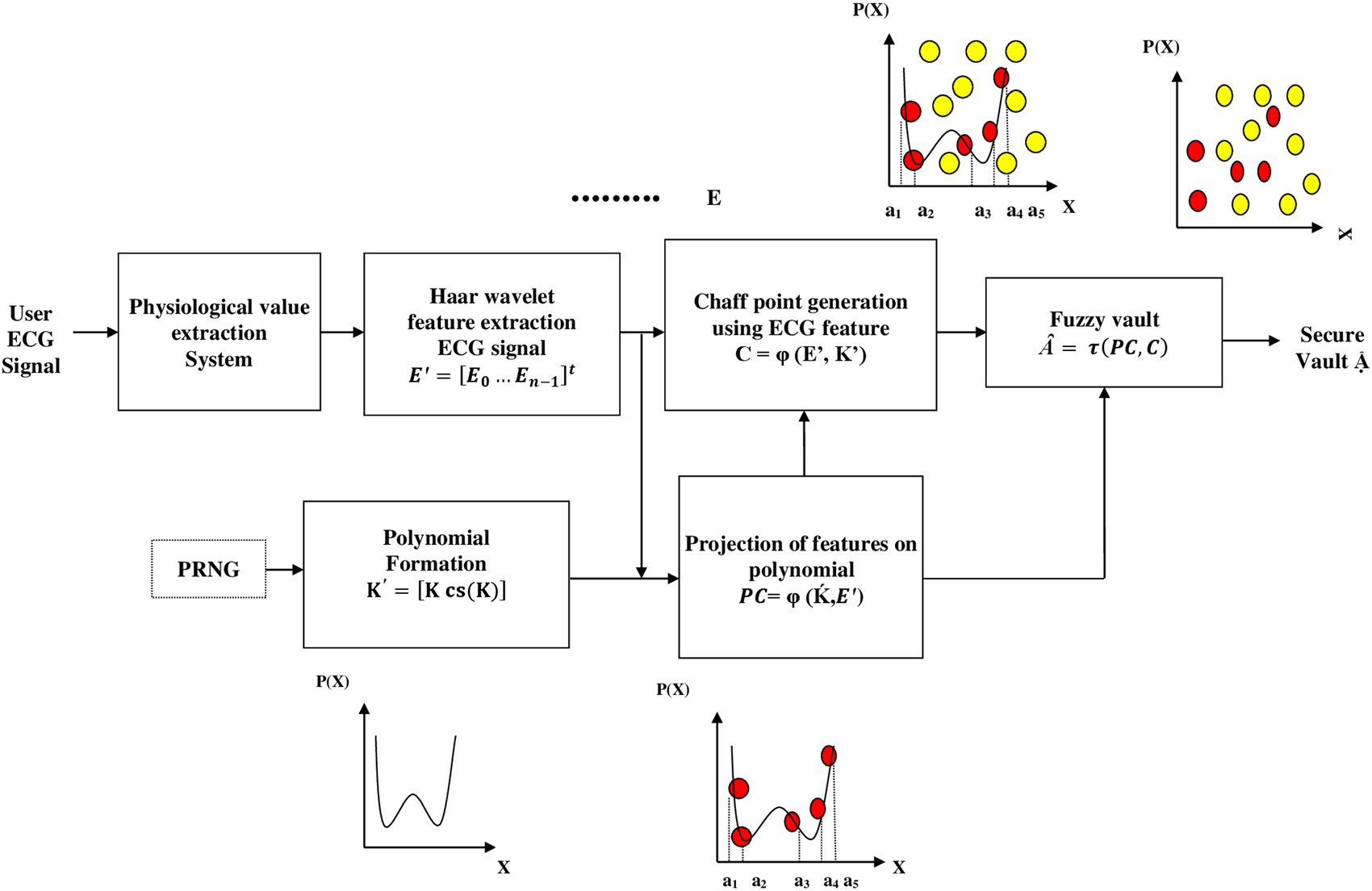
特征向量锁定阶段的框图如（图2）所示。生物信号 特征提取系统包含心电信号处理算法，用于提取Q、R和
S特征，其中取自用户心电坐标的峰值（Xw j, Y w j）以列 矩阵形式表示，E由下式给出
E=[E0E1......En−1] t (4)
其中En=[Xwj，Ywj]。Xwj是峰值点的x轴坐标，Ywj是有 效点中从输入心电信号找到的最大峰值点数。每个心电 信号峰值坐标随后被连接起来，形成用于构建FV的x轴 值。该数据集被绘制到公式（3）中的PE Q(x)上，以获 得相应的y轴值Ywj。此输入构建的多项式集合由下式给 出
PC= φ(K′, E) (5)
其中 φ是将ECG有效点绘制在多项式集合上的多项式构 造函数。这是一个比公式(6)中的ECG矩阵更长的简单行 矩阵。
PC=[PC1.PC2......PCu] t (6)
系统中的下一个过程是生成诱饵（噪声）点C的模块，用 于生成诱饵点。提取的生理值（PV），即患者ECG信号 的有效点，以及密钥K被用作生成诱饵点的参考值。这是因为诱饵点在隐藏于有效点内部时具有不可区分的特性， 从而为密钥协商提供安全性，如公式(7)所示。
C= ψ(K′, E) (7)
其中 ψ是生成矩阵C中候选诱饵点的诱饵点生成函数。
每个候选诱饵点坐标（Cxi, Cyi）用于诱饵点生成。该过 程持续进行，直到生成足够数量的干扰点。通常，干扰 点的数量至少要与特征向量中的有效点保持1:10的比率。
已知干扰点的生成是特征向量中最耗费计算资源且最耗 时的任务。为了降低这一开销，提出了使用RPSC进行诱 饵点生成。所生成的诱饵以一维矩阵形式表示，如下所 示：
C=[c1 c2 ......cκg −1]
t (8)
其中，Ci 是诱饵点的值集合，(κ) 是诱饵点生成的最小 倍增比率。
这些诱饵点与PC结合，以混淆（隐藏）有效点集。
在XY平面中，有效点和干扰点的组合形成特征向量Â， 如公式(9)和(10)所示。
Â= τ(PC, C)=[PC, C] t
(9)
Â=[PC1.PC2......P Cuc1c2......cg−1] (10)
其中 τ是特征向量构造函数，用于在干扰点内绘制有效 点。通过与有效点集共同生成的干扰点具有更高的相似 性，使攻击者难以识别密钥K。随后，特征向量通过无线 信道传输给编程器，该密钥协商方案旨在确保特征向量 与干扰点之间传输时密钥的安全性。干扰点的基数根据 所需安全性而变化；其中数量越大（如1:12），破解保险 库的难度越高。保险库通过有效点解锁，密钥的提取将 在下一节中讨论。

模糊保险箱解锁阶段

在解码阶段，使用认证的PV解锁保险库以恢复密钥K。
在接收端，编程设备通过感知的心电信号特征提取有效 点，这由以下给出
ρ=[ρ0 ρ 1 ........ρμ − 1] (11)
其中 ρμ − 1 是 (ρx j , ρ yj) 的元组。 ρ x j 是第 j 个有效点的 x 轴坐标，ρ yj 是第 j 个有效点的 y 轴坐标。接下来
利用这些有效点，通过应用RPSC生成诱饵点，并与接收 到的特征向量结合，以便在编程器端去除诱饵点。然后 将特征提取后的有效点集与特征向量进行匹配，以找到 最近匹配的保险库成员，并识别出保险库点。获取并解 锁集合生成模块的操作由以下步骤给出
η= R(Â, ρ, δ)
(12)
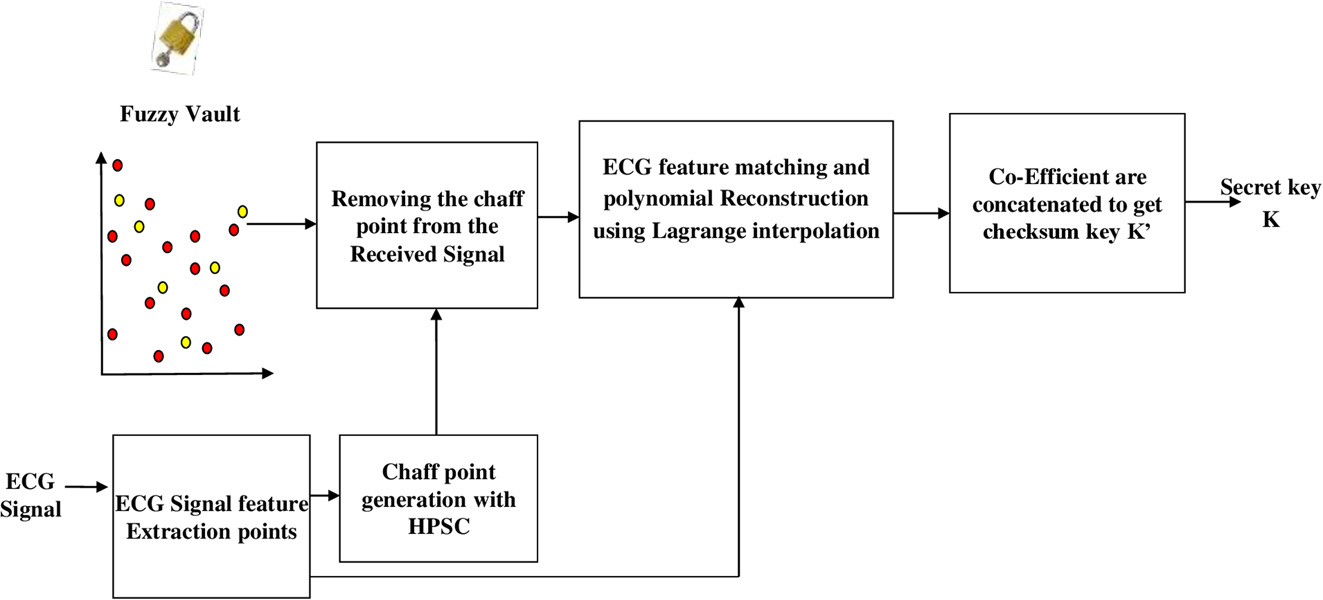
其中，R 是心电信号特征匹配函数。心电信号特征集 ρ 与接收到的模糊保险箱 Â 进行匹配，以寻找最近匹配的 保险库成员， δ 为常数值，表示正匹配时两者之间的最 大允许距离。（图3）展示了接收端编程设备中模糊保险 箱解锁阶段的流程。随后，先前的心电信号有效点集 ρ 被替换为一个新集合，该集合包含最近的保险库成员及 其对应的 y 轴坐标。
η= [η0 η 1 ............ ηη − 1] (13)
其中η j 是(xη j, y η j)的元组。xη j是由有效点的x轴坐标和y
轴坐标连接而成的x轴坐标，而yη j是保险库成员的y轴坐 标，其可能位于
多项式。它旨在利用拉格朗日插值，基于 η有效点重构 PE。了解有效点 η可通过线性组合实现多项式的重构。
其余的坐标集被发送到多项式重建模块，以求解多 项式系数。为了成功重建多项式，至少需要 η组坐标， 否则解码过程将失败，因为其中一些坐标集可能是由噪 声点而非真实的生物特征数据生成的。多项式重建模块 尝试利用拉格朗日插值法，基于保险库中的点来重建 PE Q(x)。
在拉格朗日插值中，为了求解多项式的系数，所有 设备都知道n次度，需要n+ 1个唯一投影来求解正确的 多项式。构造的多项式Q∗(x)如下所示
Q*(x)=(x −y′ 2)(x −y′ 2)......(x −y′ n+1)
(y′ 1 −y′ 2)(y′1 −y′ 3)......(y ′ n+1)
w′ 1+ …+…
(x −y′ 1)(x −y′ 2)......(x −y′ n)
(a′ n+1 − a′ 1)(a ′ n+1 − a′ 1)......(a ′ n+1 − a′ 1)
w′ n+1
(14)
方程(15)的解是
Q∗ (x)= h∗ nx n+ h∗ n−1x n−1+…h ∗ 0 (15)
其中，系数 h0 ∗、h1 ∗......hn ∗ 被提取并计算其校验和值。
该值与附加在末尾的发射器校验和值进行比较，一旦匹 配成功，多项式的系数将被连接以形成密钥K，并存储以 供后续使用
安全目的。这些程序不仅允许解锁保险库，还提供了发 送端与接收端之间的数据隐私和设备认证。用于诱饵点 生成的RPSC算法将在下一节中讨论。该算法减少了计算 量，并降低了诱饵点生成的执行时间。

建议的RPSC阶段

FV是一种在植入式医疗设备（IMD）与编程器之间具有 抗噪声能力的密钥共享模型。在此情况下，起搏器（ IMDs）用于感知心电信号[20]。RPSC包含两个主要阶 段：第一阶段是从心电信号中提取有效点Q、R和S点， 即唯一峰值点的特征提取，该阶段包括两个步骤，分别 为平滑处理和哈尔小波变换（WT）。第二阶段是提出的 RPSC算法用于诱饵点生成。心电信号的主要特征是五个 峰值点P、Q、R、S和T。首先，IMD和编程器均采集 10–15秒（∼ 14次心跳）的心电信号[21]。记录的信号以 每秒360个采样、每通道11位分辨率、10毫伏范围进行数 字化转换。使用MATLAB R2015a对心电信号进行预处 理，并提取Q、R和S点的峰值幅度（xi）。第一阶段通过 中值滤波器对心电信号进行平滑处理，以降低噪声，保 持波形的高度和形状，并去除记录心电信号[22]过程中产 生的其他噪声。第二阶段将预处理后的心电信号作为哈 尔小波变换（WT）的输入。

第一次迭代后点的移动。(C) 在2n中实现全局点 d 迭代。（D）所有花粉的比率每个全局峰值。常数参数为切换概率 S=0.8 和 L´evy 飞行 λ=1.5。)

小波变换（WT）提供了 21–25层的Haar小波分解 [23]。对心电信号进行五层分解，提取出P、Q、R、S和 T等独特点。为了确保分析的准确性，仅将其中的QRS波 峰值点（称为有效点）从用户的心电信号中分割并提取 出来。随后从心电信号中检测出Q、R和S点的幅值及其 坐标位置（xi, yj）。这些坐标以数组形式录入Excel表格 （excel.xls）中。利用MATLAB从心电信号中提取有效 点的平均计算时间为0.12秒，峰值点占用内存为54MB。
（表1）显示了心电信号中Q、R和S波峰值的唯一幅值 （xi）值。这些峰值被载入树莓派3发射器和接收端模块 中。将从心电信号中提取的Q、R和S点幅值等特征提取 峰值点作为XY平面中的有效点，并在XY全域图中作为诱 饵点生成的参考点[24, 25]。从心电信号中获取的Q、 R和S波峰值的幅值（xi）被传递至下一阶段（硬件设备）， 并作为生成干扰点的参考值，如（表1）所示。
下一节将详细介绍在树莓派3上使用RPSC算法生成 诱饵点及密钥协商方案的硬件实现细节。

RPSC算法

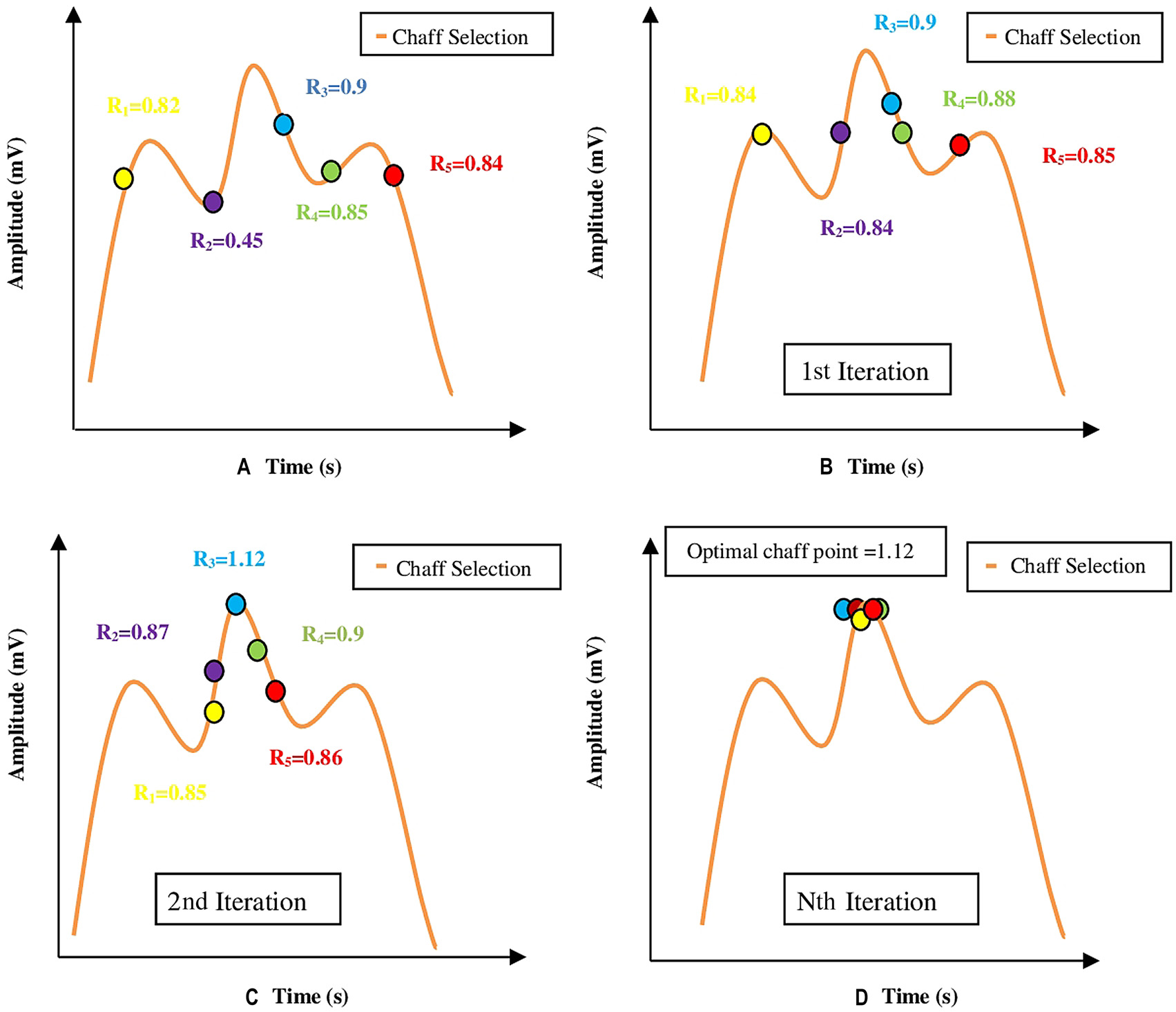
密钥K和由生理值PV生成的有效点不足以在密钥协商方 案中为特征向量FV提供安全性。诱饵点C是额外添加的 虚拟点，以生理值PV为参考创建，用于增强特征向量 FV的安全性。在RPSC算法中，候选诱饵点向诱饵点选 择过程的移动如（图4）所示。
从心电信号中提取生理值Q、R和S点峰值，并将其 归类为有效点。提取14个Q、R和S峰值点，最多获得42 个峰值点，称为有效点。一旦通过RPSC算法提取出有效 点，这些有效点将作为参考点用于生成诱饵点，具体步 骤如下[26]。
步骤1 ：假设在完整的幅度‐时间（A‐T）曲线上随机生成 五个候选诱饵点R 1 ,R2 ,R3 ,R4 ,和R5 。通过计算候选诱饵点 与参考点之间的距离来评估
适应度函数并表示为 R1=0.82、R2=0.45、R3=0.9、R4=0.85 和 R5=0.84，如（图4A）所示。
步骤2 ：一旦评估了候选诱饵点的适应度函数，最大距离 点即为全局峰值=“gpeak”点，其位于R3=0.9。
步骤3 ：在RPSC算法中，切换概率（sp=0.8）值决定候 选点必须进行全局或局部点搜索。全局和局部点搜索简 要说明如下。
在第一次迭代中，点 R1, R 3, R4, 和 R5 进行全局点搜 索，而 R2 进行局部点搜索，以到达下一次迭代的新位置。
全局点搜索 ：在第一次迭代中，R1 , R3 , R4 , 和 R5 进 行全局点搜索。首先考虑 R4 候选诱饵点进行全局点搜索， 候选诱饵点的下一个最优位置根据两条向量轨迹的合成 结果进行更新。此处，由莱维飞行[27] 给出的第一个向 量方向被绘制
从一个随机的莱维分布中生成，该分布沿一个向量方向 呈高斯分布。另一个向量方向指向当前的“gbest”。合 成向量轨迹方向即为第一次迭代结束时候选诱饵点的下 一个最优位置。该新位置的更新如（图4B）所示。
局部点搜索 ：在第一次迭代中，R2点在两个相邻的 候选诱饵点方向之间进行局部点搜索。R1点位于一个方 向，而R3点位于另一个向量方向。合成向量指向新的方 向，到达下一个最优位置。这是下一次迭代中点R2的新 位置，新位置如图4B所示。
步骤4 ：在第一次迭代结束时，全局最优解“gbest”的 位置已从R 3 =0.9移动到R 4 =0.88。以新的位置点和新的 “gbest”为参考，更新候选诱饵点的位置。
步骤5 ：在第二次迭代结束时，RPSC算法将最大峰值点 识别为R3=1.12，如图4C所示。
步骤6 ：在后续迭代中，RPSC算法更快地收敛到最大峰 值点，并达到全局峰值振幅点。这种更快的收敛速度是 由于在单个阶段同时进行了全局和局部点搜索，以及列 维分布的小步长和切换概率所致（如图4D所示）。
RPSC最适合用于诱饵点生成应用，因为它在单次迭 代[28]中既探索全局点又利用局部点。随后，将全局点的 峰值幅度转换为相对于参考有效点的诱饵点位置。该无 效点生成过程同时针对所有R波峰值点和Q波峰值点进行。
一旦生成干扰点，它们将与特征向量合并并传输至接收 设备。该RPSC算法的优点在于计算复杂度较低。

RPSC算法复杂度

在类似于嵌入式系统的硬件上实现时，考虑操作的逻辑 开销，对算法进行了复杂度分析。构建复杂模型所需的 基本逻辑操作包括加法器、减法和乘法器。减法操作与 加法器类似，其复杂度为O(n)。所有高阶操作，如除法 和平方根运算，都是基于这些基本操作构建的。加法操 作具有O(n)的线性复杂度。由此可得，乘法和平方操作 的复杂度相似，均为O(n2)。除法逻辑采用牛顿‐拉夫逊 [29]方法设计，构建时使用了四个乘法器和三个加法器， 并将复杂度值表示为O(n)=4n2+ 3n。最后但同样重要的 是，在所有计算机算法中最常用的比较器和随机数生成 器操作符也被设计出来，两者的复杂度均为O(1)。诱饵 点生成算法的性能由如下所示的复杂度分析确定

No.	操作	复杂度	总计
1.	i=0，t=0，初始化随机点 S=0.8, δ=0.01, λ=1.5。	0	t*
2.	n* while (t<G)//迭代//	1	n*1
	For (i=1; i<S; i++)//候选诱饵点大小//	S*(1+n)	Sn +Sn²
	rand=RNG (0.1)	1	n*1
			Sn²+Sn + 2n
3.	n* if (rand>p)//全局点搜索//	1	n*1
	Zp þ1 f ¼ Zp f þHðb* Zp f Þ	3	n*3
	H=(λ Γ(λ) sin(πλ/2) /π)*(1/SZ (1+ λ ))	3	n*3

No.	操作	复杂度	总计
			7n*
4.	否则//局部点搜索//	n*
	ε=RNG (0,1)	1	n*1
	Zp þ1 f ¼ Zp f þЄðZp v Zp s Þ	3	n*3
			4n*
5.	n* for (i=1; i<S; i++)	S*(1+n)	Sn +Sn²
	如果 ( Zp f > Zp þ 1 f )	1	n*1
	b∗¼ Zp f//当前最佳//	0	0
			Sn²+Sn +n
6.	Else	0
7.	t++	n	n
	总复杂度，O(n) ：		t* +Sn²+ Sn+ 2n + 7n + 4n + Sn²+ Sn+n + n = 2Sn²+ 2Sn+ 15n + t*
			∼ 2Sn²+ 2Sn + 15n
			∼O(n²)

（表2）。克莱西算法的复杂度分析为立方级O(n³)，而 哈利尔算法提出的诱饵点生成算法计算出其复杂度逻辑 值为O(n²)。RPSC算法在诱饵点生成方面的算法复杂度 已计算得出，其复杂度为O(n²)。与克莱西的诱饵点生成 模型相比，RPSC算法由于减少了候选诱饵点的计算，性 能有所提升。
由于减少了候选诱饵点的计算，RPSC算法的性能得 到了提升。在下一节中，将对诱饵点生成的执行时间进 行模拟。

使用MATLAB对RPSC进行性能评估

MATLAB代码模拟了实时工作场景，并针对不同的诱饵 点值进行了执行。候选诱饵点从最小到最大值运行，生 成的总干扰点及其执行
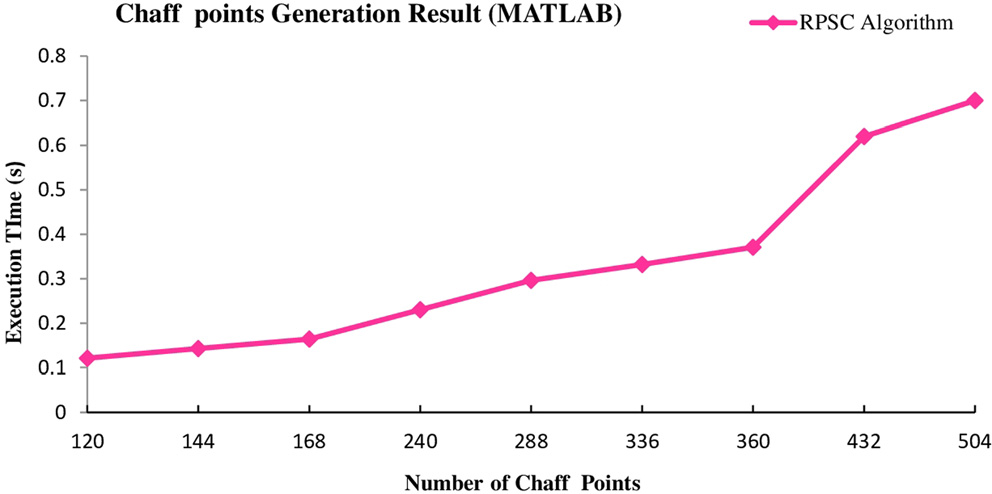
记录了时间。生成的诱饵点值分为三个阶段。第一阶段 最多为672个候选诱饵点。在此范围内生成候选诱饵点并 从中选择诱饵点所需的最短时间为0.121–0.164秒。第二 阶段考虑从672到1,344个候选诱饵点的范围。在此范围 内生成候选诱饵点并从中选择诱饵点，RPSC算法所需的 最短时间为0.23–0.371秒。在最后阶段，生成最多504个 干扰点所需的最大时间为0.7秒。表3展示了总干扰点与 执行时间的三种不同比率的测量结果。

生成的诱饵点最少数量为120个，耗时0.121秒，且 执行时间随生成的诱饵点数量线性增加。系统生成504个 诱饵点的最大执行时间为0.7秒，此时生成了2,016个候选 诱饵点。这意味着更短的执行时间可形成一种节能模型。
所有这些不同的诱饵点生成方式在（图5）中展示了 详细的视图，候选诱饵点的数量随着诱饵点数量的增加 而增加。这间接表明，诱饵点数量的增加会提升保险库 安全性，但也会直接增加系统的执行时间。

RPSC候选诱饵点比较

RPSC算法生成的候选诱饵点F数量较少，候选点数量少 导致执行时间减少。要获得C个诱饵点，需要随机生成 F个候选诱饵点。（表4）展示了各种诱饵点生成模型与 RPSC的比较。在RPSC算法中，候选诱饵点总数F随诱饵 点数量的增加而线性增加，与其他模型相比增长更为平 缓。当所需诱饵点数量为100时，RPSC生成的候选诱饵 点数量高于克莱西和阮等人，但低于哈利勒算法。当诱 饵点数量增加到200时，RPSC算法生成的候选诱饵点数 量少于克莱西和哈利勒，且与阮等人的数值相等。还可 以明显看出，当诱饵点数量超过200后，其他模型的数值 呈指数级增长。
当候选诱饵点计数F增加到240时，通过克莱西和哈 利勒方法生成的候选点数量分别为66,609和117,605，数 量较高，而阮方法生成了3,276个候选干扰点。

表3：有效点、候选诱饵点和干扰点生成的不同层次及执行时间。
序号	候选诱饵 点生成	诱饵点 生成	时执间行（秒）
1.	480	120	0.121
2.	576	144	0.143
3.	672	168	0.164
4.	960	240	0.23
5.	1,152	288	0.296
6.	1,344	336	0.332
7.	1,440	360	0.371
8.	1,728	432	0.62
9.	2,016	504	0.7

RPSC算法仅生成1,152个候选点，分别比克莱西、哈利 勒和阮氏方法小57.82倍、102倍和2.84倍。其他研究未 给出生成504个诱饵点所需的候选诱饵点数量，但 RPSC算法中生成了近2,540个干扰点。与其他模型相比， RPSC算法生成的候选诱饵点数量显著更少。该算法通过 减少候选点的生成数量，降低了整体计算时间，使所提 出的RPSC模型成为轻量级模型。RPSC算法在不降低系 统性能和安全性的前提下，为单个有效点生成最多数量 的候选诱饵点（1:12）。一旦生成诱饵点，它们将与有效 点和密钥K结合形成特征向量。

RPSC执行时间的比较

使用RPSC对不同诱饵数量下的诱饵点生成时间进行评估， 并获得每次生成的执行时间。
将所提出的RPSC方法与各种技术（阮等人、哈利勒 等人、克莱西等人）的执行时间进行比较。改进后的性 能结果如（表5）所示。随着诱饵点数量的增加，克莱西 等人、哈利勒等人和阮等人的执行时间呈指数级增长， 而RPSC算法则线性增加。RPSC结果表明，在生成504个 诱饵点时，其加速性能比克莱西高出206倍，比哈利尔算 法高出130倍，比阮的现有算法高出93倍。

生成的诱饵点数量变化时的执行时间
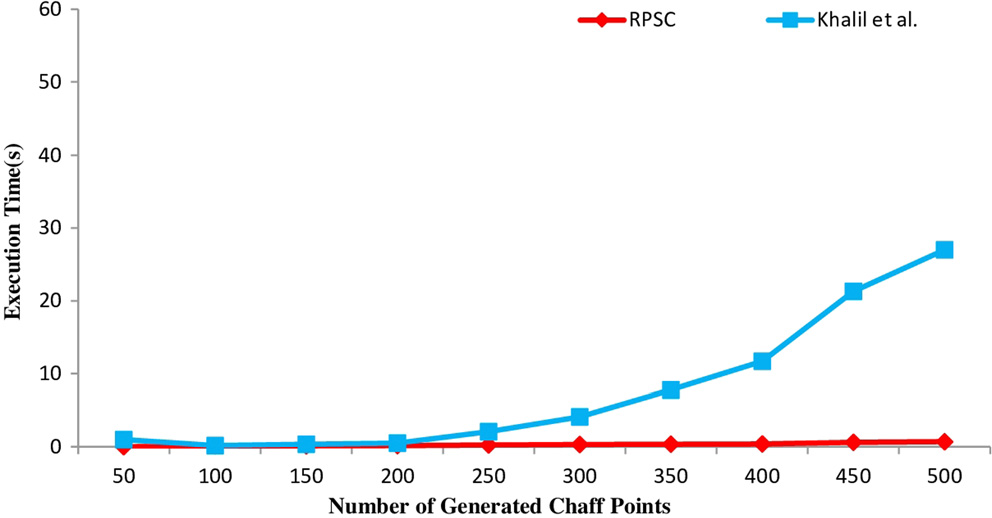
在（图6）中展示了RPSC和哈利尔算法在不同数量生成 的诱饵点下的执行时间。
RPSC算法能更快地收敛到诱饵点，从而在安全模型 上消耗更少的时间和能量。RPSC在诱饵点生成过程中包 含两个操作：全局和局部点搜索均在迭代中完成。其次， 由于调参数量较少，收敛到下一个最优解的速度很快。
该过程非常迅速，可在0.121秒内生成120个干扰点。所 模拟的诱饵点生成算法在树莓派3独立系统上运行，并对 其性能进行了评估。

所提诱饵点算法在树莓派3处理器上的性能表现

基于完整心电信号的诱饵点生成算法在树莓派3系统级芯片 板上实现。该板卡配备1GB内存、1.2吉赫兹ARM处理器， 功耗为2.5–10 W，属于低功耗设备。树莓派3运行树莓派操 作系统

表 4：使用提出的RPSC算法与克莱西、哈利勒和阮生成的候 选诱饵点的比较。
编号	有效 点	诱饵 点	候选干扰点数量
			克莱西 等人	哈利勒 等人	阮等人
10	100	191	607	154	480
20	200	2358	4809	918	960
24	240	66,609	117,605	3276	1152
42	504	*N/A	*N/A	*N/A	2016

表 5：干扰点生成方法的性能。
诱饵数量 点	克兰西的	哈利勒	哈尼的 Hanh	阮
100	0.3633	0.167	0.09	0.122
150	1.02	0.367	0.208	0.143
200	2.006	0.5	0.3088	0.164
250	3.51	2.08	0.8219	0.233
300	6.123	4.1	2.7575	0.296
350	9.5	7.8	–	0.332
400	14.94	11.67	–	0.371
450	24.12	21.3	–	0.61
500	37.97	27	–	0.7

在处理器上，通过Python和Java算法实现特征向量锁定、 解锁、诱饵点生成与去除。这些树莓派3模型内置无线独 立模型，已证实适用于广泛的电子医疗保健应用[30]。来 自MIT‐BIM数据库的心电信号在主机计算机中进行处理， 提取出唯一的Q、R和S点（Xi, Y j）坐标后，发送至树莓 派3处理器[31]。使用两个处理器，其中一个作为树莓派 3发射器（起搏器），另一个作为树莓派3接收器（外部 编程器），并配有主机编程器，如（图7）所示[32]。

在生成干扰点之前，需对各板卡进行时间同步，以 产生相似的诱饵模式

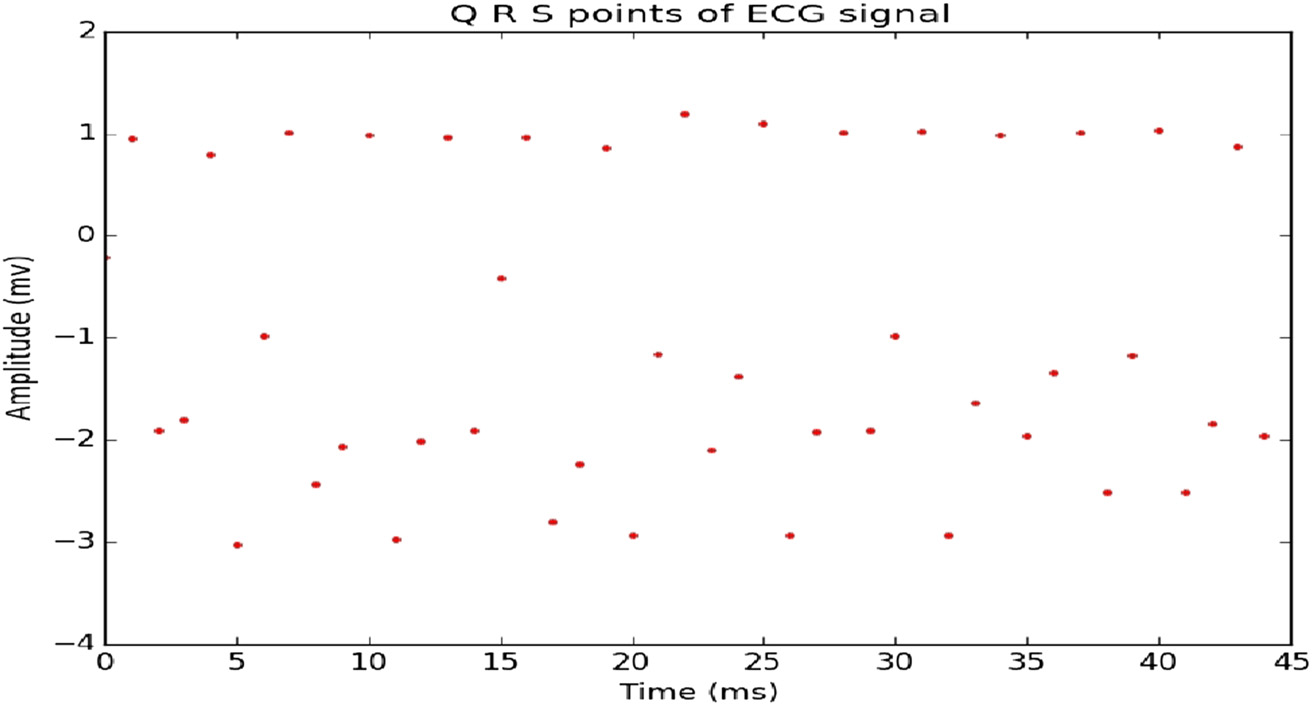
点。在树莓派3中加载的心电信号由处理器根据幅度和时 间进行绘制，如图8所示。
特征向量在无线介质中从发射器传输到接收端树莓 派3并被锁定，如（图9）所示。发射模块展现了密钥的 特征向量锁定的各个阶段。
将下载的心电信号加载到树莓派3上后，根据心电信 号的Q、R和S点作为最大值和最小值点，基于RPSC算法 生成诱饵点。
诱饵点与心电信号结合，最后由树莓派3根据生成的 密钥K和PRNG算法组合形成特征向量FV并进行传输 （起搏器）。发射器树莓派3处理器在硬件上以不同层级 的诱饵点C生成和不同迭代级别运行，并测量其执行时间 和数据速率（表6）。

特征向量被远端接收端树莓派3接收，主机计算机下载 的心电信号用于提取Q、R和S点。基于这些点通过应用

表 6：1000、800、600、400 的各种迭代级别，a nd 200。
参数	有效：诱饵点 比率 (1:20)	有效：诱饵点 比率 (1:16)	有效：诱饵点 比率 (1:12)	有效：诱饵点 比率 (1:8)	有效：诱饵点 比率 (1:4)
种群大小 Ps	100(候选诱饵点 点)	80(候选诱饵点 点)	60(候选诱饵点 点)	40(候选诱饵点 点)	20(候选诱饵点 点)
总数 诱生饵成的点	840	672	504	336	168
迭代 i=1,000
总干扰点 生成时间(秒)	98.90	68.40	41.88	22.99	12.41
模糊保险库大小	6,106字节	4,916字节	3,746字节	2,582字节	1,436字节
比特率	6.0千比特/ 秒	4.8 kb/s	3.7 kb/s	2.5 kb/s	1.4 kb/s
迭代 i=800
总干扰点 生成时间（秒）	81.335	55.316	34.52	21.299	11.459
模糊保险库大小	6,097字节	4,907字节	3,774字节	2,576字节	1,433字节
比特率	6 kb/s	4.8 kb/s	3.7 kb/s	2.5 kb/s	1.4 kb/s
迭代 i=600
总干扰点 生成时间（秒）	63.45	44.26	28.39	16.82	9.621
模糊保险库大小	6,125字节	4,931字节	3,751字节	2,575字节	1,431字节
比特率	6.0千比特/ 秒	4.9千比特/ 秒	3.7千比特/ 秒	2.5 kb/s	1.4 kb/s
迭代 i=400
总干扰点 生成时间（秒）	43.88	33.23	22.05	13.47	8.73
模糊保险箱大小	6,124字节	4,926字节	3,744字节	2,581字节	1,425字节
比特率	6.0千比特/ 秒	4.9千比特/ 秒	3.7 kb/s	2.5 kb/s	1.4 kb/s
迭代 i=200
总干扰点 生成时间（秒）	26.52	19.29	14.31	10.49	7.844
模糊保险库大小	6,119字节	4,941字节	3,758字节	2,580字节	1,430字节
比特率	6.0 kb/s	4.8 kb/s	3.7 kb/s	2.5 kb/s	1.4 kb/s

RPSC中的干扰点C是基于心电信号本地生成的干扰点。
通过接收到的信号，将本地生成的Q、R和S点以及干扰 点进行抵消。一旦去除这些点，剩余的数据即为密钥， 并从中提取出特征向量。该密钥由外部编程设备用于在 两个设备之间安全地共享数据。同时可知，一旦建立物 理接触并生成密钥，该密钥仅可用于本次会话。当物理 接触断开后，先前的密钥将无法继续使用，从而提升了 信息的安全性。因此，通过上述在树莓派3硬件上实现的 过程，在实时场景中实现并完成了安全密钥协商方案的 通信。
（表6）中的实验结果直接影响系统的计算、内存和 通信开销。我们观察到，在种群大小固定且保险库大小 固定的条件下，随着迭代次数的变化，特征向量大小增 加，候选诱饵点数量也随之增加。
在（图10）中可以观察到，当候选种群大小为20且 在不同迭代级别下，执行时间呈线性增长。进一步观察 发现，当候选诱饵点数量增加时，执行时间也线性增加。
因此，随着候选诱饵点数量的增加，执行时间随之增加， 这间接表明当通过诱饵点数量提高安全性时，所需时间 也随之增加。结论是，随着候选诱饵点数量和迭代次数 的增加，诱饵生成时间呈线性增长。同时观察到，当候 选大小增加时，处理器的计算量和功耗也随之增加。
RPSC算法在树莓派3上的执行时间高于其在MATLAB仿 真中的运行时间。该RPSC算法的实现与仿真在合理的时间内生成了大量干扰点，同时高效地完成了计算密集型 的诱饵点操作，提升了密钥协商方案的安全性。

讨论与结论

该RPSC通过在特征向量中生成大量诱饵点来增强IMD与 编程器之间的安全通信。通过提出一种计算量更小且诱 饵点生成算法，并减少候选诱饵点的数量，从而降低了 执行时间。复杂度分析表明，RPSC算法的复杂度为 O(n²)，这是一个显著的
相较于现有方法在O(n³)上的表现有所改进，从而提高了 整体系统效率并降低了IMD的电池消耗。MATLAB执行 结果表明，该方法减少了候选诱饵点的数量和复杂度。
该方法在较短的0.7秒计算时间内最多可生成504个干扰 点，相比现有算法速度更快。接下来，对在RPi3处理器 上实时实现的RPSC密钥协商方案和干扰点生成算法进行 了分析。使用RPSC后，硬件中大量候选诱饵点所占用的 内存也显著减少。在最大迭代次数为1,000、种群大小为 20的设置下，实际可在98.90秒的生成时间内最多生成 840个干扰点，展示了在真实独立硬件中的编码效率和能 力。第一阶段重点是在MATLAB中利用RPSC进行干扰 点生成，通过大范围的候选诱饵点规模提升WBAN的安 全性，实现设备认证和密钥协商方案，以确保设备间实 时通信的安全，并降低执行时间。第二阶段挑战中，通 过RPi3设备将FV无线传输至接收端。采用增强的低计算 量干扰点生成算法，在硬件实现中成功达成了安全传输 密钥的目标，满足了安全性与设备认证的需求。未来计 划将提出的安保模型应用于多个无线设备间的通信，并 进一步扩展其在医疗运动设备中的部分通信功能。