LeetCode初级算法31：将有序数组转换为二叉搜索树_二叉树输出[0,-3,9,-10,null,5]-优快云博客

这篇博客介绍了如何将已排序的整数数组转换为高度平衡的二叉搜索树。通过选取数组中间元素作为根节点，递归地构建左右子树，确保每个节点的左右子树高度差不超过1。提供的代码展示了具体的实现过程，适用于解决数据结构和算法问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

🐕 给你一个整数数组 nums ，其中元素已经按升序排列

请你将其转换为一棵高度平衡二叉搜索树。

高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

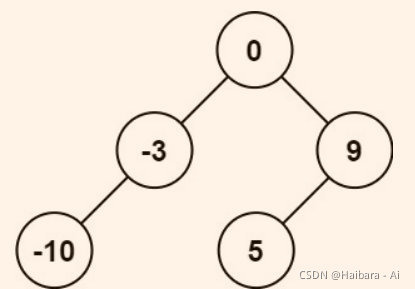
在这里插入图片描述

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
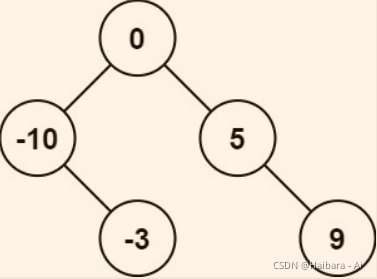
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

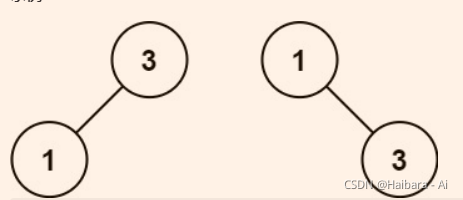
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 10的4次方
-10的4次方 <= nums[i] <= 10的4次方
nums 按严格递增顺序排列

思路：都已经排序好了不就是分成左中右三部分么？

每次取数组的中间位置的数做root 左边的数做root的左子树右边的数做root的右子树

上代码

public static TreeNode sortedArrayToBST(int[] nums) {
    	if(nums.length == 0) {
    		return null;
    	}
    	// 将数组放入递归中
    	return process(nums,0,nums.length-1);
    }
    public static TreeNode process(int[] nums , int start , int end) {
    	// 先判断 start 和 end 的条件
    	if(start > end) 
    		return null;
    	// 求数组中点位置 做 root
    	int mid = start + ((end - start) >> 1);
    	TreeNode root = new TreeNode(nums[mid]);
    	// 设置root的 左右子树
    	root.left = process(nums,start,mid-1);
    	root.right = process(nums,mid+1,end);
    	// 返回 root
    	return root;
    }