二叉树的非递归遍历

前面一篇介绍了二叉树的递归遍历操作 http://blog.itpub.net/29876893/viewspace-1841619/，下面介绍二叉树的非递归遍历操作。
运用递归操作，很容易进行二叉树的遍历，结合上篇文章的介绍，在递归的时候都是找到当前结点，压入”栈“中，然后再通过当前结点找到左（右）孩子，递归函数每次返回时，当前结点都会出”栈“。在非递归遍历时，那就构造一个栈，用来存取每个结点的指针，通过该结点找到（左）右孩子，思路是有了。
下面结合下图简单的说明一下：

                                                                                               

          

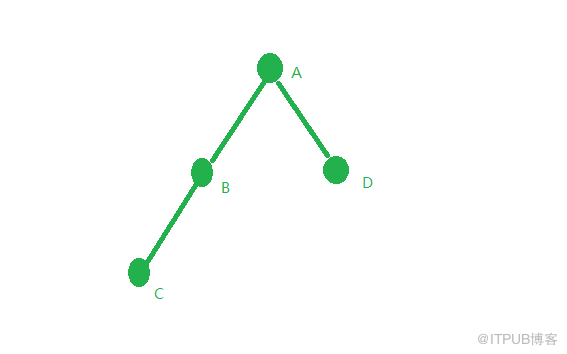前序遍历：
首先A,B,C依次入栈，然后由于C->lchild为空，所以返回到结点C,遍历其右孩子C->rchild,但是也为空，此时C出栈，遍历B结点的右孩子，为空，B出栈，返回到A,A出栈，遍历A结点的右孩子，打印D的数据域，D进栈，遍历D的左孩子，为空，D出栈，遍历D的右孩子，为空，此时栈也空，该循环结束。
中序遍历：
首先A,B,C依次入栈，然后由于C->lchild为空，所以返回到C,打印C结点的数据域，然后遍历C->rchild,由于为空，C出栈，返回到B,打印结点B的数据域，然后遍历B->rchild,由于为空，B出栈，返回到A,A出栈，打印结点A的数据域，然后遍历A->rchild,不为空，然后遍历D->lchild，为空，返回到D,D出栈，打印D结点的数据域，然后遍历D->rchild,由于为空，此时栈为空，循环结束。
后序遍历：
A,B,C依次入栈，第一次遍历这些结点时，设置了标记，都为0.然后遍历C->lchild,为空，此时返回C,设置标记为1，然后访问C->rchild,由于为空，此时C出栈，打印了C结点的数据域。下面也是这样分析，由于过程复杂，读者可以自己分析，这里不作赘述。
下面给出上述的实现代码：

点击(此处)折叠或打开

1. #include<iostream>
   
2. #define MAX_SIZE 20
   
3. using namespace std;
   
4. typedef struct TreeNote {
   
5.     char ch;
   
6.     struct TreeNote *lchild, *rchild;
   
7. }*BiTree;
   
8. typedef struct Stack {
   
9.     BiTree data[MAX_SIZE];
   
10.     int top;
    
11. };
    
12. 
    
13. void createBiTree(BiTree &bt) {
    
14. 
    
15.     char chh;
    
16.     cin >> chh;
    
17.     if (chh == '#')
    
18.         bt = NULL;
    
19.     else {
    
20.         bt = new TreeNote;
    
21.         bt->ch = chh;
    
22.         createBiTree(bt->lchild);
    
23.         createBiTree(bt->rchild);
    
24.     }
    
25. }
    
26. void initStack(Stack *&st) {
    
27.     st = new Stack;
    
28.     st->top = -1;
    
29. }
    
30. bool emptyStack(Stack *st) {
    
31.     return st->top == -1;
    
32. }
    
33. bool fullStack(Stack *st) {
    
34.     return st->top == MAX_SIZE - 1;
    
35. }
    
36. void pushStack(Stack *st, BiTree bt) {
    
37.     if (!fullStack(st))
    
38.         st->data[++st->top] = bt;
    
39.     else
    
40.         cout << "栈已满!" << endl;
    
41.     // exit(-1);
    
42. }
    
43. BiTree pop(Stack *st) {
    
44.     if (!emptyStack(st)) {
    
45.         return st->data[st->top--];
    
46.     }
    
47.     else
    
48.         return NULL;
    
49. }
    
50. BiTree getpop(Stack *st) {
    
51.     if (!emptyStack(st)) {
    
52.         return st->data[st->top];
    
53.     }
    
54.     else
    
55.         return NULL;
    
56. }
    
57. void preOrderTree(BiTree bt) {
    
58.     Stack *st;
    
59.     initStack(st);
    
60.     BiTree p;
    
61.     p = bt;
    
62.     while (p != NULL || !emptyStack(st))
    
63.     {
    
64.         while (p != NULL)
    
65.         {
    
66.             cout << p->ch << " ";
    
67.             pushStack(st, p);
    
68.             p = p->lchild;
    
69.         }
    
70.         if (!emptyStack(st))
    
71.         {
    
72.             p = pop(st);
    
73.             p = p->rchild;
    
74.         }
    
75.     }
    
76. }
    
77. void InOrderTree(BiTree bt) {
    
78.     Stack *st;
    
79.     initStack(st);
    
80.     BiTree p;
    
81.     p = bt;
    
82.     while (p != NULL || !emptyStack(st)) {
    
83.         while (p != NULL) {
    
84. 
    
85.             pushStack(st, p);
    
86.             p = p->lchild;
    
87.         }
    
88.         if (!emptyStack(st)) {
    
89.             p = pop(st);
    
90.             cout << p->ch << " ";
    
91.             p = p->rchild;
    
92.         }
    
93.     }
    
94. }
    
95. void postOrderTree(BiTree bt)
    
96. {
    
97.     BiTree p;
    
98.     Stack *st;
    
99.     initStack(st);
    
100.     p = bt;
     
101.     int flag[20];
     
102.     while (p != NULL || !emptyStack(st))
     
103.     {
     
104.         while (p != NULL)
     
105.         {
     
106.             pushStack(st, p);
     
107.             flag[st->top] = 0;
     
108.             p = p->lchild;
     
109.         }
     
110.         while (!emptyStack(st) && flag[st->top] == 1)
     
111.         {
     
112.             p = pop(st);
     
113.             cout << p->ch << " ";
     
114.         }
     
115.         if (!emptyStack(st))
     
116.         {
     
117.             flag[st->top] = 1;
     
118.             p = getpop(st);
     
119.             p = p->rchild;
     
120.         }
     
121.         else break;
     
122.     }
     
123. }
     
124. int main() {
     
125.     TreeNote *bt;
     
126.     cout << "please input some values:" << endl;
     
127.     createBiTree(bt);
     
128.     cout << "preOrderTree:" << endl;
     
129.     preOrderTree(bt);
     
130.     cout << endl;
     
131.     cout << "InOrderTree:" << endl;
     
132.     InOrderTree(bt);
     
133.     cout << endl;
     
134.     cout << "postOrderTree:" << endl;
     
135.     postOrderTree(bt);
     
136.     cout << endl;
     
137. }

运行结果：

来自 “ ITPUB博客 ” ，链接：http://blog.itpub.net/29876893/viewspace-1848850/，如需转载，请注明出处，否则将追究法律责任。

转载于:http://blog.itpub.net/29876893/viewspace-1848850/