53. 最大子序和

53. 最大子序和

题目描述

给定一个整数数组 nums，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释:连续子数组[4,-1,2,1] 的和最大，为6。

进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

实现1 - 暴力法

思路

从前向后遍历，找出以当前元素为起点的连续子数组的最大值，和之前找到的最大值比较，取得当前最大值。

class Solution {
    public int maxSubArray(int[] nums) {
        int max = Integer.MIN_VALUE;
        
        for(int i=0; i<nums.length; i++) {
            int curMax = nums[i];
            int sum = nums[i];
            for(int j=i+1; j<nums.length; j++) {
                sum = sum + nums[j];
                if(sum > curMax) {
                    curMax = sum;
                }
            }
            
            if(curMax > max) {
                max = curMax;
            }
        }
        
        return max;
    }
}

以数组只有4个元素为例，图中的0，1，2，3是数组的下标，当需要计算以下标0为起点的连续子序列的最大值，需要从0开始计算到最后一个值（就是以根节点子节点为根的子树）；当需要计算以下标1为起点的连续子序列的最大值，需要从1开始计算到最后一个值，以此类推，最后比较以数组的所有节点为起点的连续子数组的最大值（就是比较每个根节点的子节点）。

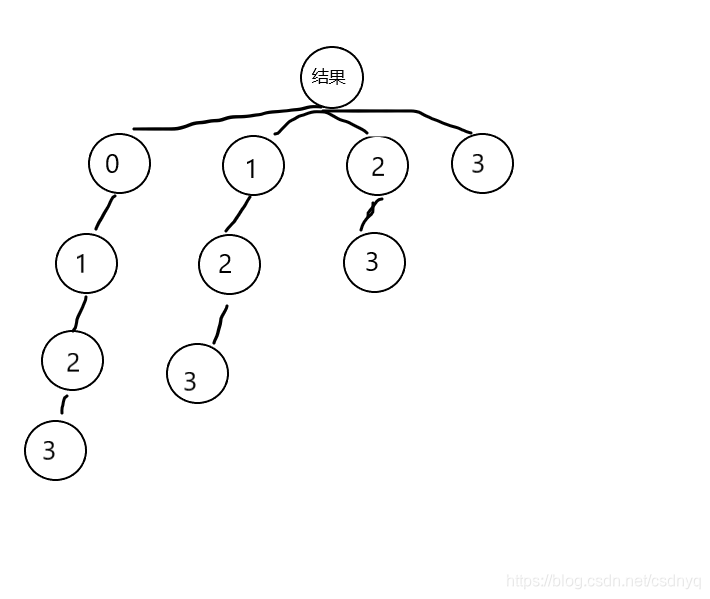
时间复杂度是 O(n^2)，循环 n 次，每次要比较 (n - 1) 次。

实现2 - 动态规划

从图中可以看出，暴力法的问题是大量的重复计算，可以用备忘录存储计算出来的值，这里就不写备忘录的解法，直接使用 dp table。

状态转移方程：

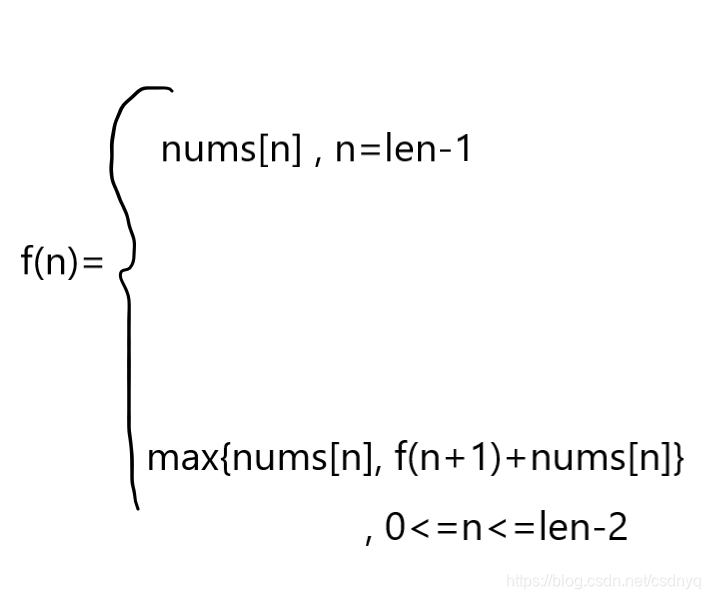
class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        dp[nums.length - 1] = nums[nums.length - 1];
        int max = dp[nums.length - 1];
        
        for(int i=nums.length-2; i>=0; i--) {
            dp[i] = Math.max(nums[i], dp[i + 1] + nums[i]);
            
            if(dp[i] > max) {
                max = dp[i];
            }
        }
        
        return max;
    }
}

时间复杂度：O(n)