本文来源公众号“萝卜大杂烩”,仅用于学术分享,侵权删,干货满满。
原文链接:万字长文,Numpy入门教程!
本文给大家整理了一份绝佳的Numpy入门学习资料,文章略长,建议收藏!可以当文档使用,在需要的时候查看!
1 Numpy简介
Numpy的全称是"Numeric Python",直译为"数值Python",可以理解成它是Python的一个专注于数值运算的第三方扩展包,主要是用来处理、计算一维或者多维数组。它提供了丰富对数组的操作,比如:数学运算、数据筛选、线性代数、统计运算、随机模拟、傅里叶变换等。
随着数据科学的发展以及数据量的增加,对海量数据处理的要求也越来越高,Numpy作为Python数据分析、机器学习和数据科学的主力军,Numpy在矩阵和数组运算上有着非常不错的性能,计算速度极快。其次基于Numpy的数据处理库pandas也丰富了Numpy的使用场景。
2 数据类型
Numpy作为Python的第三方扩展包,它提供了比Python更为丰富的数据类型,下面的表格进行统计:
| 编号 | 类型 | 描述 |
|---|---|---|
| 1 | bool_ | 布尔型数据类型(True 或者 False) |
| 2 | int_ | 默认整数类型,类似于 C 语言中的 long,取值为 int32 或 int64 |
| 3 | intc | 和 C 语言的 int 类型一样,一般是 int32 或 int 64 |
| 4 | intp | 用于索引的整数类型(类似于 C 的 ssize_t,通常为 int32 或 int64) |
| 5 | int8 | 代表与1字节相同的8位整数。值的范围是-128到127 |
| 6 | int16 | 代表 2 字节(16位)的整数。范围是-32768至32767 |
| 7 | int32 | 代表 4 字节(32位)整数。范围是-2147483648至2147483647 |
| 8 | int64 | 表示 8 字节(64位)整数。范围是-9223372036854775808至9223372036854775807 |
| 9 | uint8 | 代表1字节(8位)无符号整数 |
| 10 | uint16 | 2 字节(16位)无符号整数 |
| 11 | uint32 | 4 字节(32位)的无符号整数 |
| 12 | uint64 | 8 字节(64位)的无符号整数 |
| 13 | float_ | float64 类型的简写 |
| 14 | float16 | 半精度浮点数,包括:1 个符号位,5 个指数位,10个尾数位 |
| 15 | float32 | 单精度浮点数,包括:1 个符号位,8 个指数位,23个尾数位 |
| 16 | float64 | 双精度浮点数,包括:1 个符号位,11 个指数位,52个尾数位 |
| 17 | complex_ | 复数类型,与 complex128 类型相同 |
| 18 | complex64 | 表示实部和虚部共享 32 位的复数 |
| 19 | complex128 | 表示实部和虚部共享 64 位的复数 |
| 20 | str_ | 表示字符串类型 |
| 21 | string_ | 表示字节串类型 |
3 数据类型标识码
NumPy 中每种数据类型都有自己的唯一标识的字符码,下表总结了常见的数据类型标识码:
| 字符 | 对应类型 |
|---|---|
| b | 代表布尔型 |
| i | 带符号整型 |
| u | 无符号整型 |
| f | 浮点型 |
| c | 复数浮点型 |
| m | 时间间隔(timedelta) |
| M | datatime(日期时间) |
| O | Python对象 |
| S,a | 字节串(S)与字符串(a) |
| U | Unicode |
| V | 原始数据(void) |
4 安装
下面通过实际案例来介绍快速入门Numpy。一般在安装了anaconda后便默认安装了Numpy,也可以通过其他方式安装:
pip install numpy # pip
conda install numpy # conda每次使用之前先导入:
5 导入
import numpy as np导入Numpy后国际惯例命名为np,方便后续使用。
6 查看版本信息
np.__version__
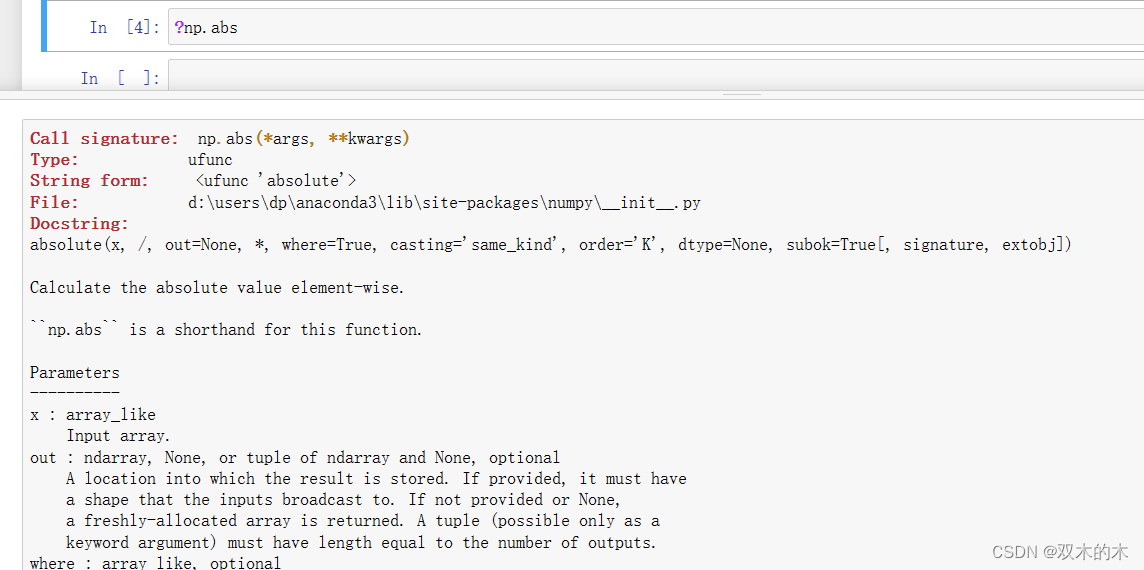
'1.21.5'7 查看帮助文档
查看Numpy中某个函数的帮助文档:
np.info(np.abs) # 查看np.abs函数的使用文档absolute(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) -------- >>> x = np.array([-1.2, 1.2]) >>> np.absolute(x) array([ 1.2, 1.2]) >>> np.absolute(1.2 + 1j) 1.5620499351813308 Plot the function over ``[-10, 10]``: >>> import matplotlib.pyplot as plt >>> x = np.linspace(start=-10, stop=10, num=101) >>> plt.plot(x, np.absolute(x)) >>> plt.show() Plot the function over the complex plane: >>> xx = x + 1j * x[:, np.newaxis] >>> plt.imshow(np.abs(xx), extent=[-10, 10, -10, 10], cmap='gray') >>> plt.show() The `abs` function can be used as a shorthand for ``np.absolute`` on ndarrays. >>> x = np.array([-1.2, 1.2]) >>> abs(x) array([1.2, 1.2])
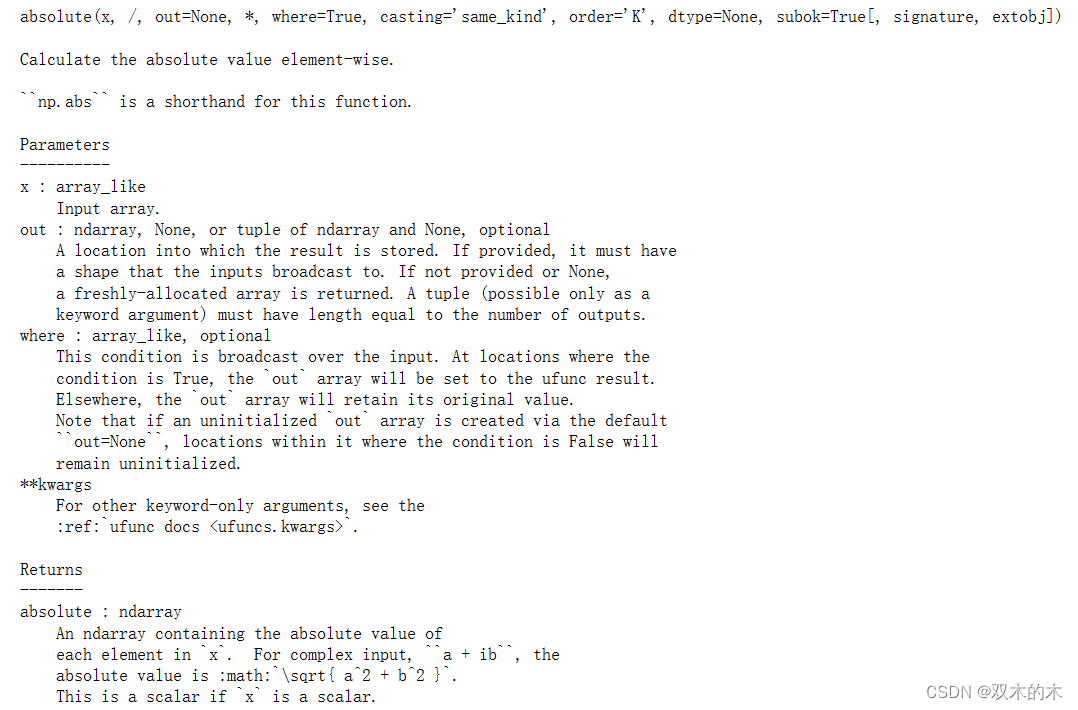

通过内省的方式也能查看函数的帮助信息:
# ?np.abs8 创建数组
8.1 np.array()
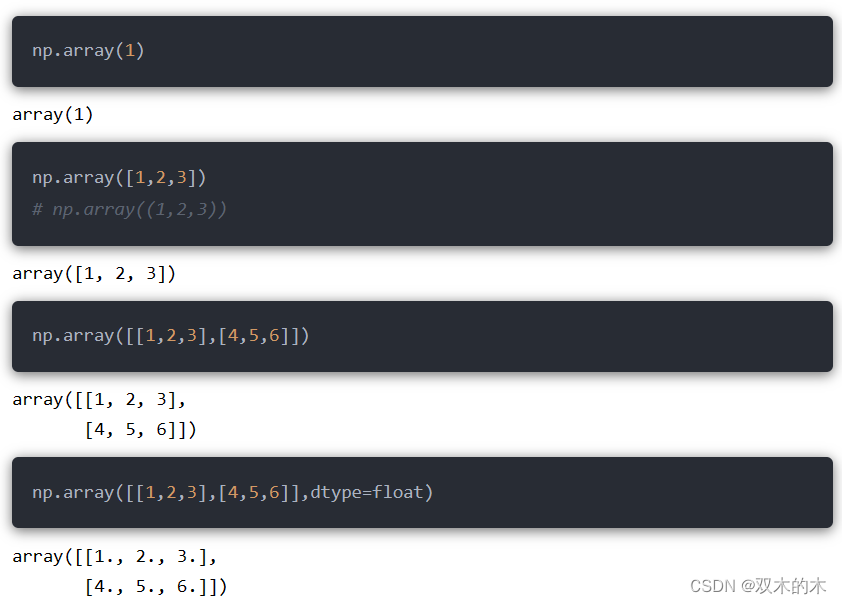
8.2 np.asarray()
np.asarray()和np.array类似,可以将一个Python序列直接转为ndarray对象:
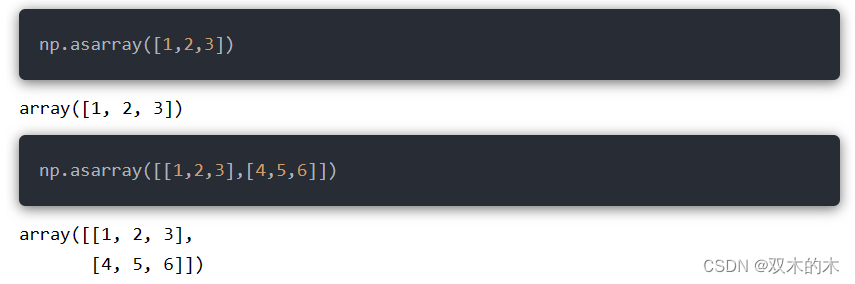
8.3 np.empty()
np.empty()是用来创建未初始化的数组,在创建的同时可以指定数组的形状和数据类型,函数语法为:
np.empty(shape,dtype,order="C")-
shape:指定生成的数组形状
-
dtype:数组元素的数据类型,默认是float
-
order:C或者F,默认是C(行优先);表示数组在计算机中的存储顺序
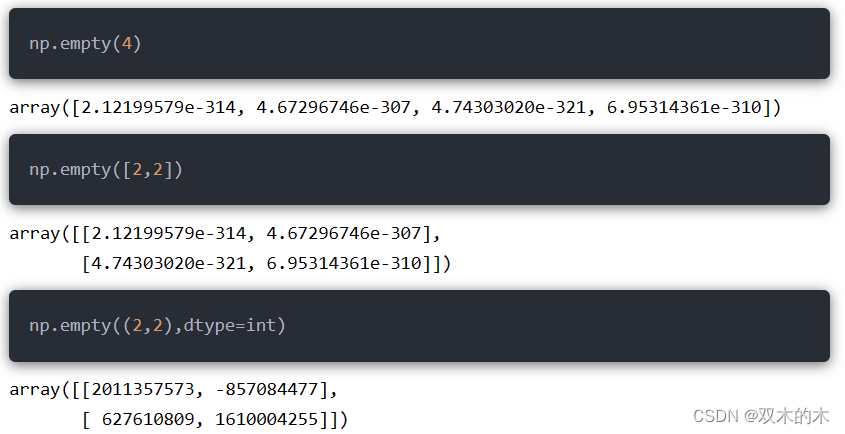
从生成的结果中可以看到,np.empty生成的数组带有随机值,没有实际含义。注意:np.empty生成的不是空数组。
8.4 np.empty_like()
创建和指定的数组相同形状shape的数组。

np.empty_like也是创建2行3列的数组:

8.5 np.zeros()
创建全部是0的向量或者数组

8.6 np.zeros_like()
创建和指定数组相同shape的全0数组:

8.7 np.ones()
创建全是1的一维或多维数组

8.8 np.ones_like()
创建和指定数组相同shape的全1数组:

8.9 np.eye()
创建指定对角线上为1,其他位置为0的矩阵。函数参数为:
np.eye(N,M=None,k=0,dtype,order)-
N:输出的行数
-
M:输出的列数,如果不指定默认和N相同
-
k:整数;如果是0,默认在主对角线上生成1;如果是正数,在主对角线上面;如果是负数,在主对角线下面;
-
dtype:生成的数据类型
-
order:C或者F,默认是C(行优先);表示数组在计算机中的存储顺序

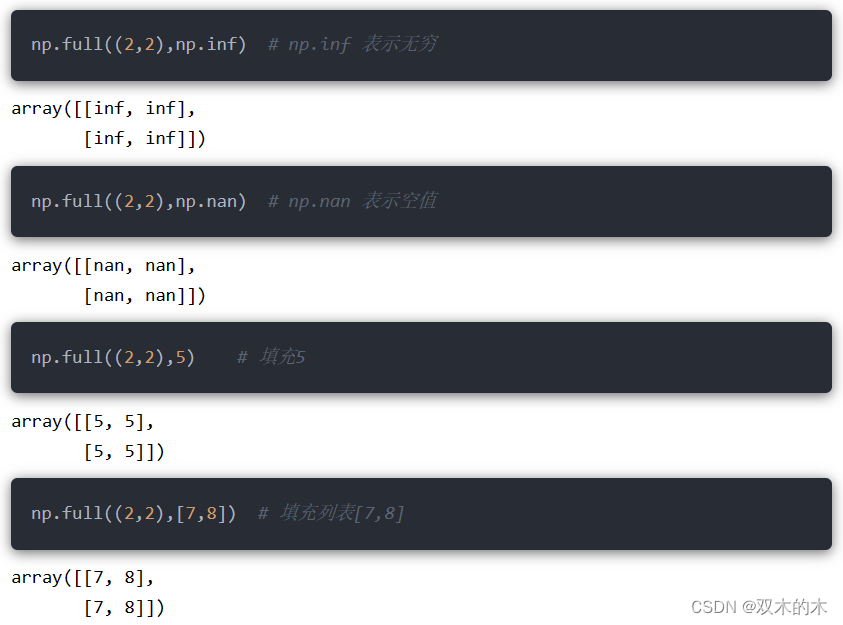
8.10 np.full()
函数参数为:
np.full(shape,fill_value,dtype=None,order="C")-
shape:数组形状
-
fill_value:待填充的值,标量或者类似数组的值
-
dtype:数据类型
-
order:C或者F,默认是C(行优先);表示数组在计算机中的存储顺序
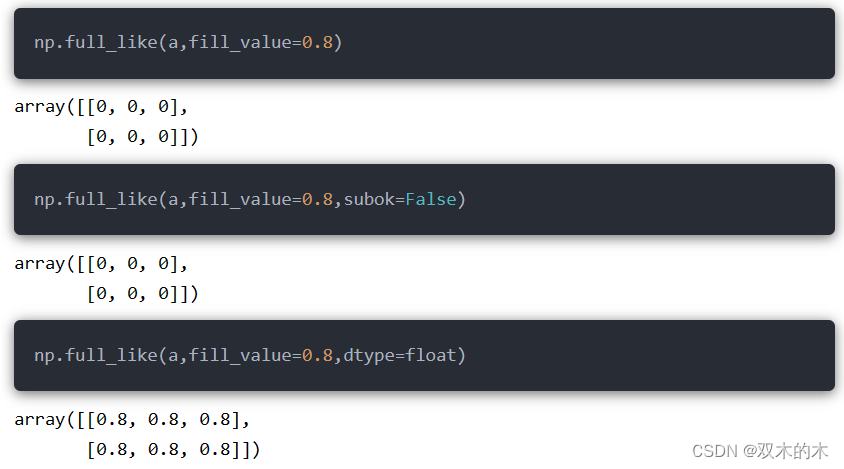
8.11 np.full_like()
函数语法为:
np.full_like(a,fill_value,dtype,order,subok=True,shape=None)-
a:指定的数组
-
fill_value:待填充的值
-
dtype:数组类型
-
order:数据存储顺序,可选为{'C','F','A','K'}
-
subok:布尔值;如果是默认True,表示生成的数组使用a的数据类型;如果是False,使用numpy内置的基础数据类型
8.12 np.arange()
函数参数为:
np.arange(start, stop, step, dtype)-
start:起始值,默认是0;包含
-
stop:终止值,不包含
-
step:步长,默认是1
-
dtype:指定数据类型

8.13 np.linspace()
表示在指定的数值区间内,返回均匀间隔的一维等差数组,默认均分50份,函数参数为:
np.linspace(start,
stop,
num=50,
endpoint=True,
retstep=False,
dtype)-
start:代表数值区间的起始值;
-
stop:代表数值区间的终止值;
-
num:表示生成多少个均匀的样本。默认值为50;
-
endpoint:默认为True,表示数列包含stop终止值,反之不包含;
-
retstep:默认为 True,表示生成的数组中会显示公差项,反之不显示;
-
dtype:表示数组元素的数据类型。
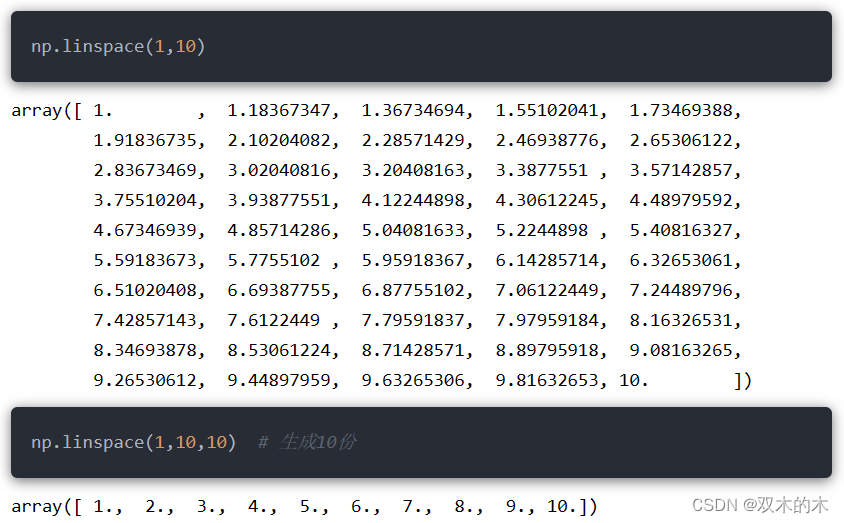
默认是包含stop值;下面的例子不包含stop10,也就是1到9生成10等份:

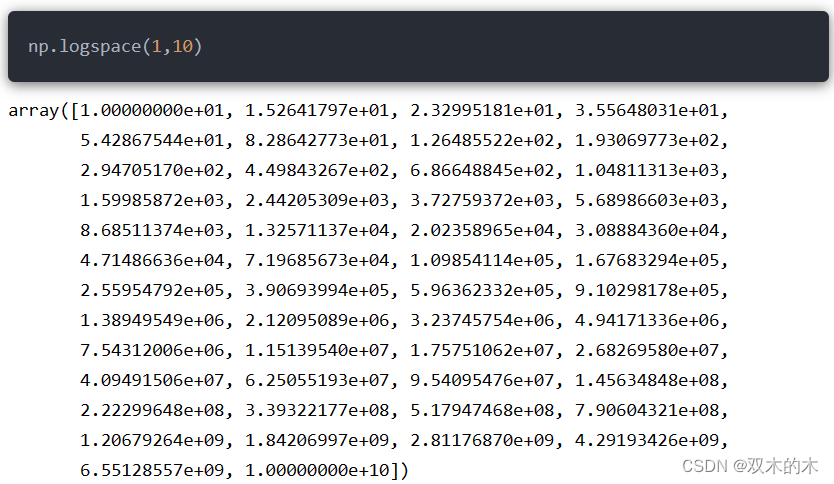
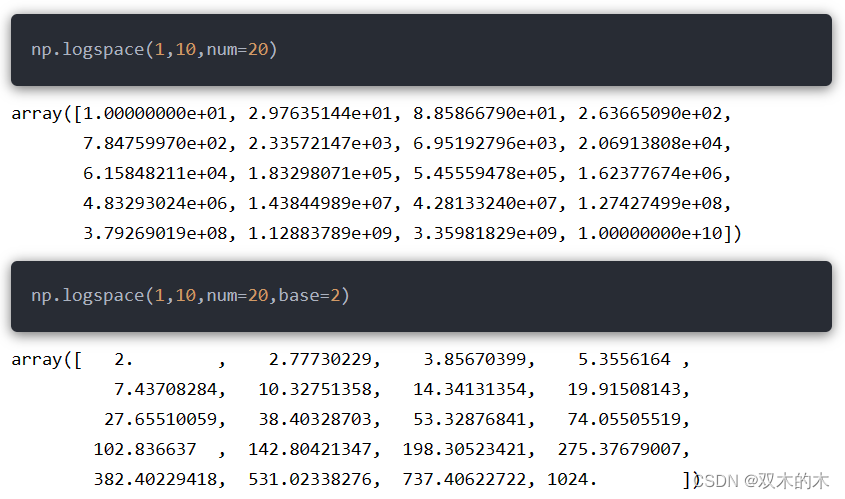
8.14 np.logspace()
表示在指定的区间内生成基于对数的等比数组,函数语法为:
np.logspace(start,stop,num=50,endpoint,base=10,dtype)参数含义类似于np.linspace函数;只有base参数表示对数函数的底数,默认是10
9 索引和切片
9.1 模拟数据
在这里模拟生成一个简单的数据:np.arange()先生成一维数组

再通过reshape函数转成指定类型的shape:
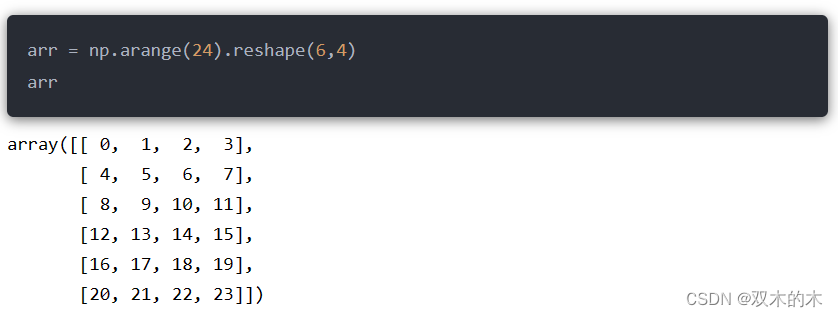
reshape函数的shape也可以使用-1;函数会自动推断(效果同上):
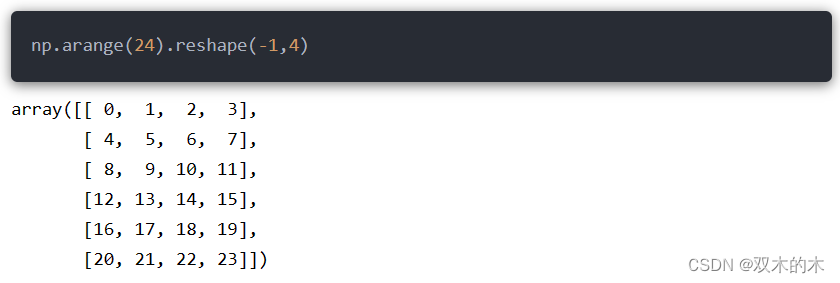
9.2 slice函数
Numpy内置的slice函数用来构造切片对象,该函数有三个参数:start(起始索引)、stop(终止索引) 和 step(步长)。

构造从1到5步长为2的切片对象:

9.3 基于切片对象
从数组arr中根据切片对象取数:

9.4 基础切片
通过冒号来分割切片;用法同python的切片相同,后文会详细介绍。

再看看其他例子:


9.5 高级切片
基于省略号...的切片方式。如果在行的位置使用省略号,表示所有行;如果在列的位置,则表示全部列。
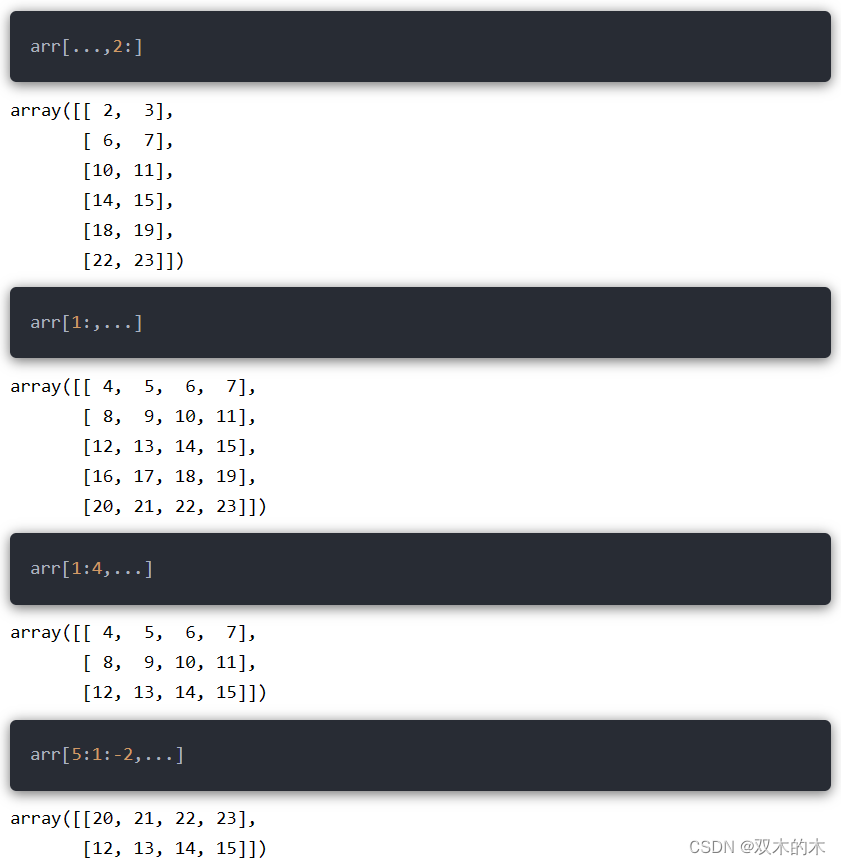
10 广播机制
广播机制旨在解决Numpy中不同shape之间的运算问题。我们知道如果两个数组shape相同可以直接运算:

在两个数组中相同位置的元素执行运算:
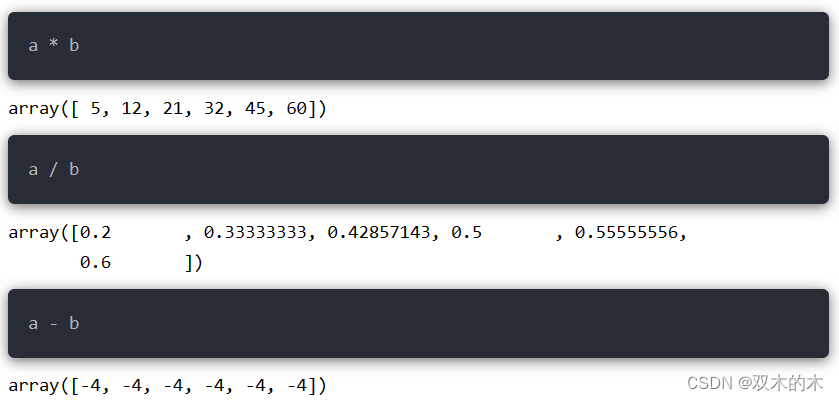
如果两个数组的shape不同呢?

相当于是把b看成:

此时和数组a的shape相同,再进行运算。
11 相关数组操作
11.1 改变形状reshape
以数组a为例:

在前文中介绍过reshape函数:

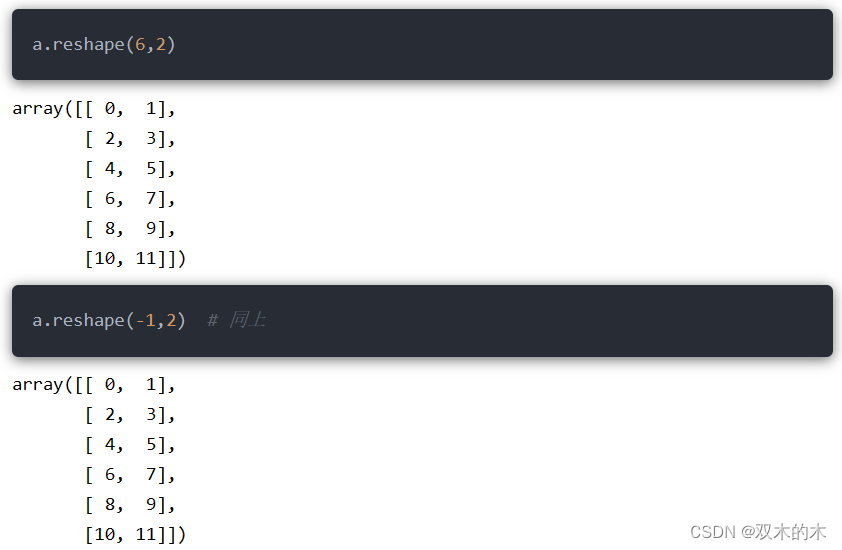
11.2 拉直数组flat
该函数返回的是一个迭代器,可以通过for循环进行遍历:
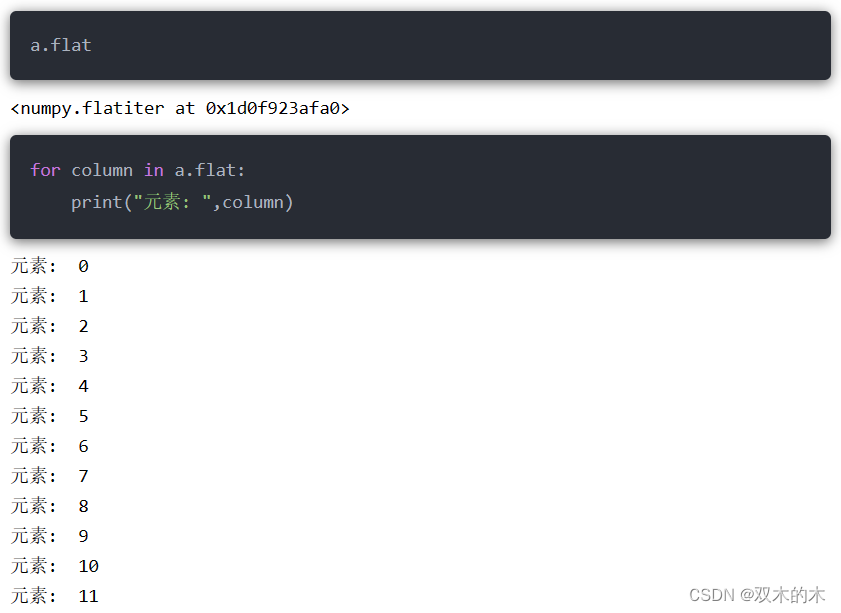
11.3 拉直数组flatten()
该函数返回的是一个数组副本,不会修改原数组,有参数:
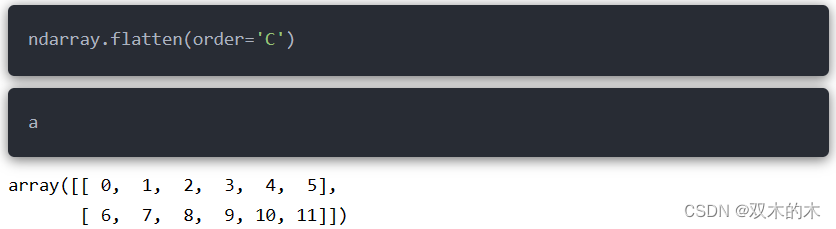
对比两种不同顺序下的结果:

11.4 数组展开ravel
np.ravel函数将多维数组的元素以一维数组的形式进行展开。如果修改会影响原数组:

11.5 转置transpose

或者使用数组的T属性:

11.6 数据滚动np.rollaxis()

12 数学运算
12.1 算术运算
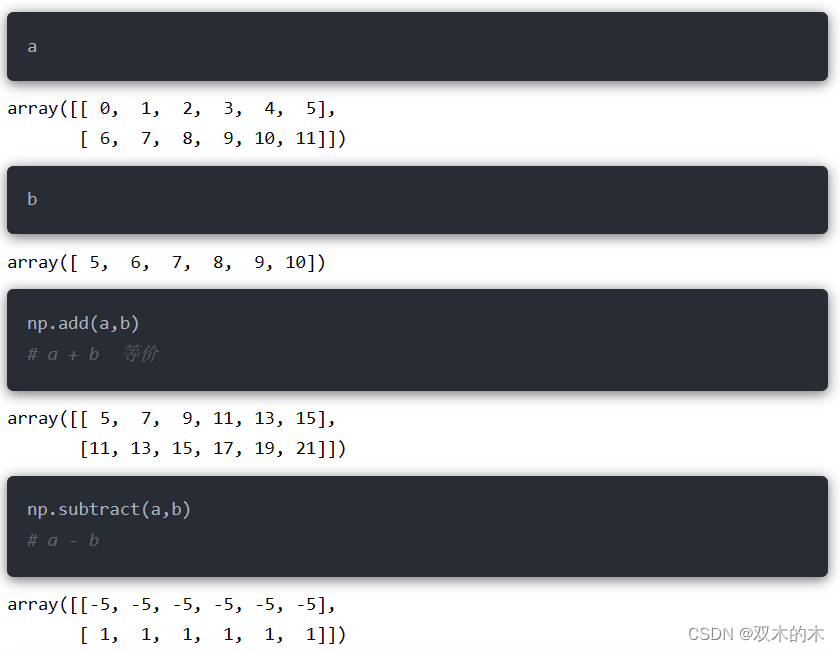
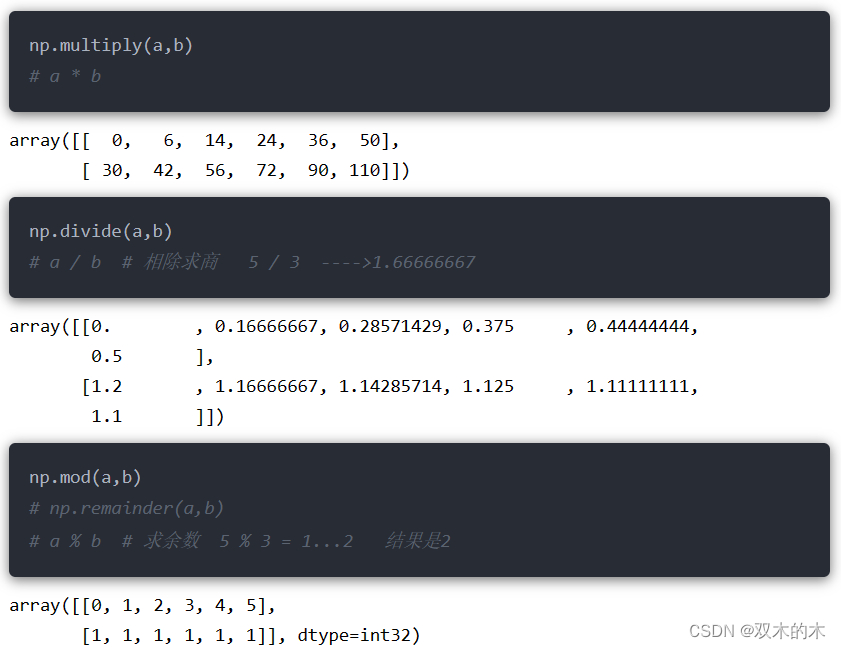
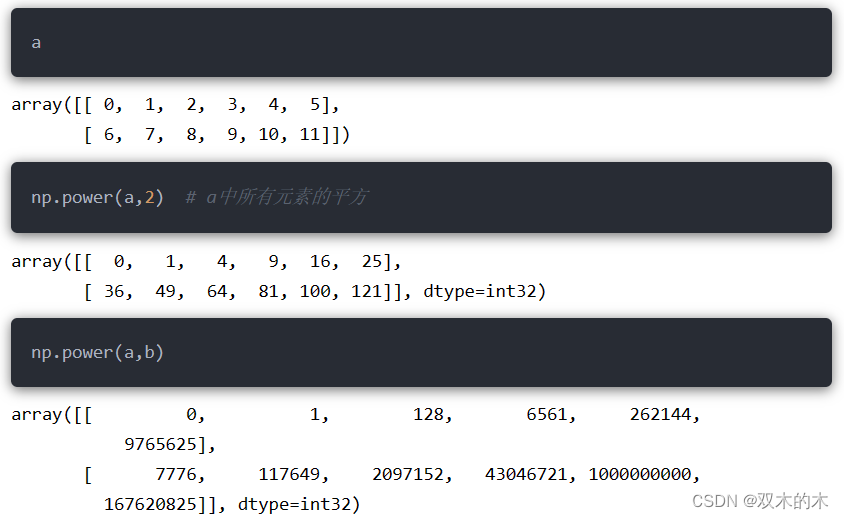
12.2 指数运算
函数语法为:
np.power(a,b)将a数组中的元素作为底数,b数组中元素作为幂,返回最终指数运算的结果:
12.3 三角函数

调用Numpy中的pi:
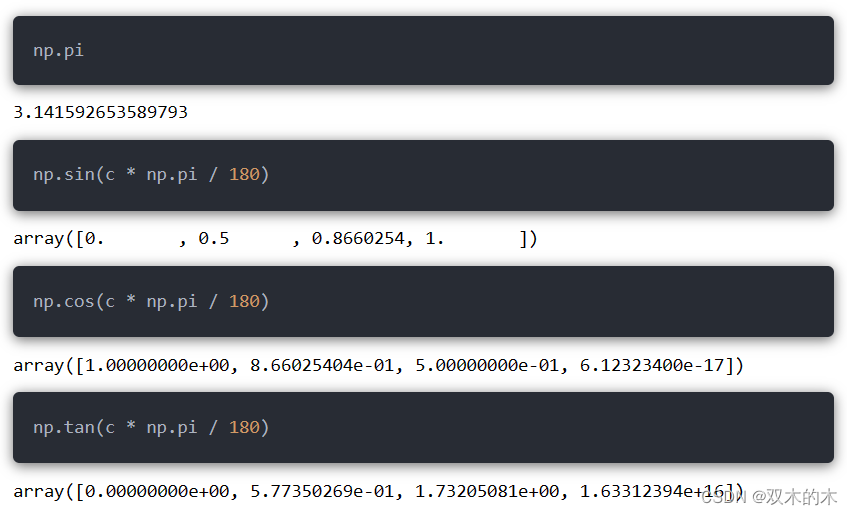
此外,NumPy还提供arcsin,arcos和arctan 反三角函数。
弧度转换功能:
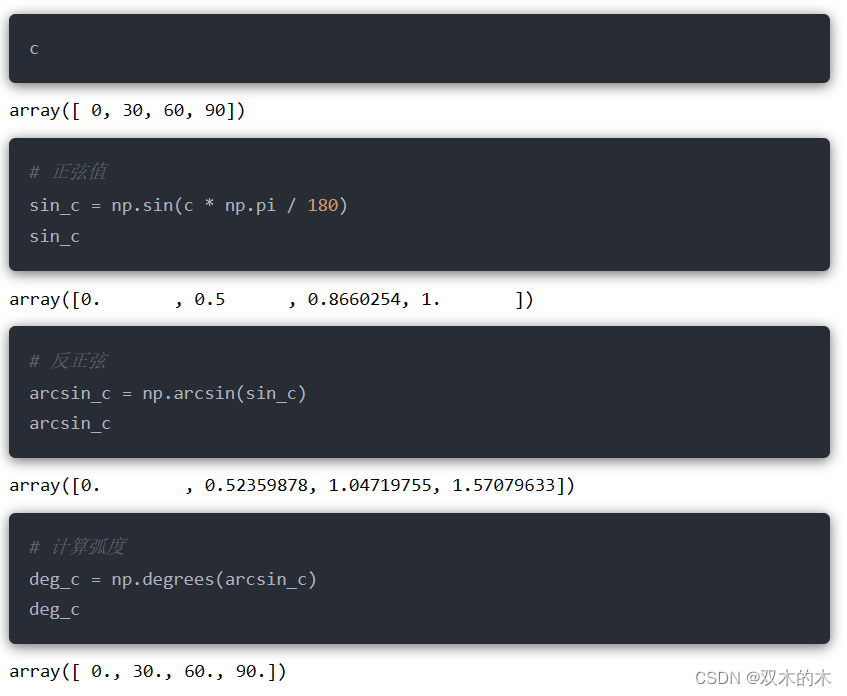
13 四舍五入
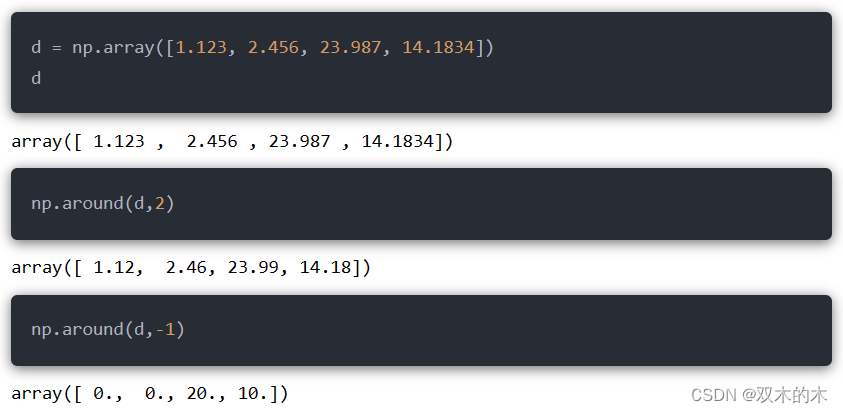
13.1 np.around()
对数值进行四舍五入,保留到指定位数:
np.around(arr,decimals)-
arr:待执行的数组或者列表等
-
decimals:指定多少位小数,默认是0;如果是负数,表示对小数点左边第n位近似
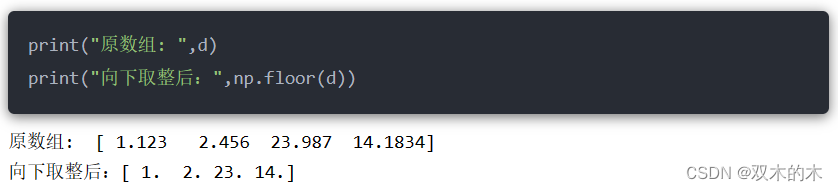
13.2 np.floor()
向下取整,即不大于数组的数值
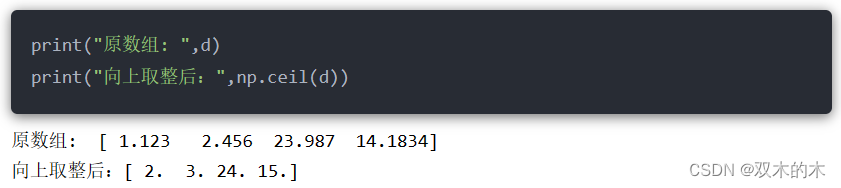
13.3 np.ceil()
向上取整,和np.floor功能相反。
14 统计函数
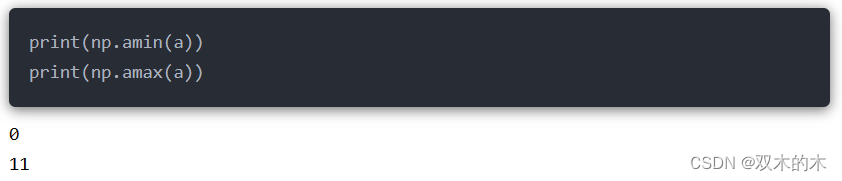
14.1 np.amin()/np.amax()
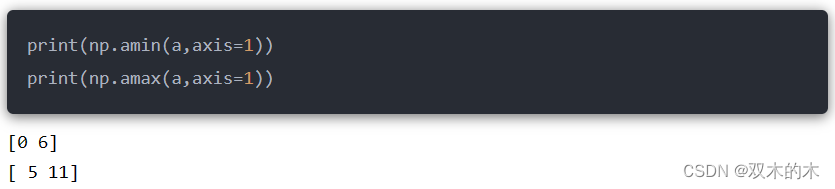
沿着指定的轴axis查找数组中的最大值或者最小值,并以数组形式返回。

整个数组中的最小值、最大值
沿着行方向-垂直方向:

沿着列方向-水平方向:
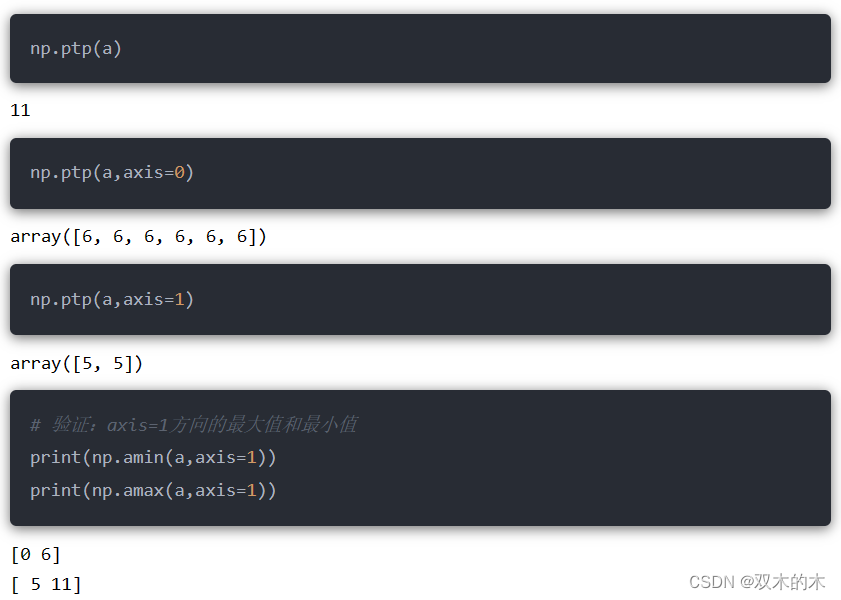
14.2 np.ptp
求最大值和最小值的差
14.3 np.percentile()
沿着指定的轴,计算任意百分比下的分位数:
np.percentile(a,q,axis)-
a:数组
-
q:指定要计算的百分位数,0-100间
-
axis:指定的轴

14.4 np.median()
计算中位数

14.5 np.mean()
计算均值

14.6 np.average()
求加权平均值

如果不指定权重,直接相加再求均值:

returned 返回权重因子之和:

14.7 np.var()
求数组的方差

14.8 np.std()
求数组的标准差

15 矩阵运算
常用的矩阵运算函数:
-
np.dot:计算两个数组的点积
-
np.vdot:计算两个向量的点积
-
np.inner:计算两个数组的内积
-
np.matmul:计算两个数组的矩阵积
-
np.det:计算输入矩阵的行列式
-
np.solve:求解线性矩阵方程
-
np.inv:计算矩阵的逆矩阵(逆矩阵与原始矩阵相乘,会得到单位矩阵)
15.1 np.dot
将其中一个数组中的每一行元素和另个数组的每列元素相乘再相加:
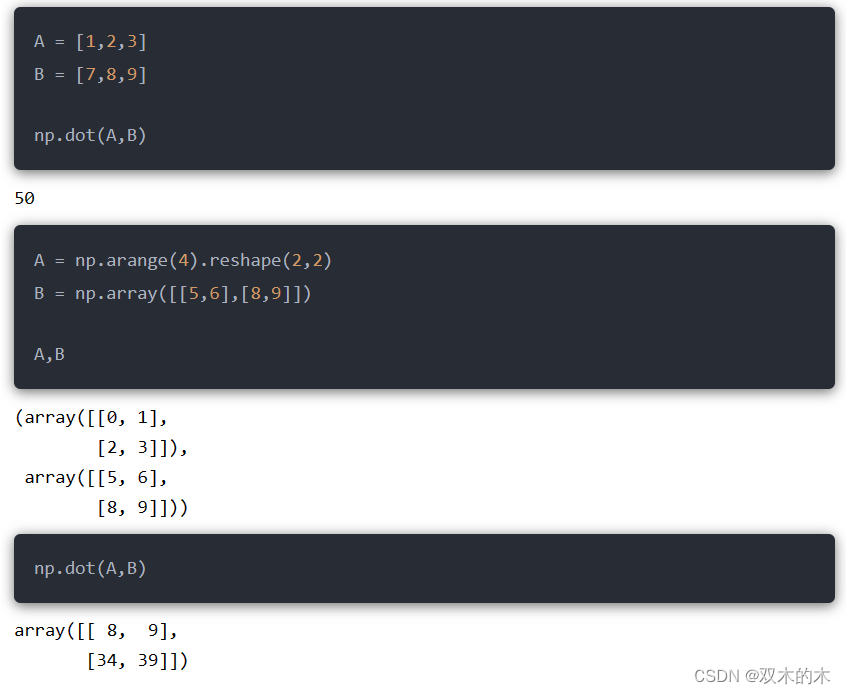
A中的每行元素乘以B中每列的元素:
# 0*5 + 1*8 = 8 # 0*6 + 1*9 = 9 # 2*5 + 3*8 = 34 # 2*6 + 3*9=39 = 34
15.2 np.vdot
计算点积结果:对应位置的元素相乘再相加

15.3 np.inner
A = [1,2,3] B = [7,8,9]
如果是一维数组,np.inner等价于np.dot:

如果是多维数组:
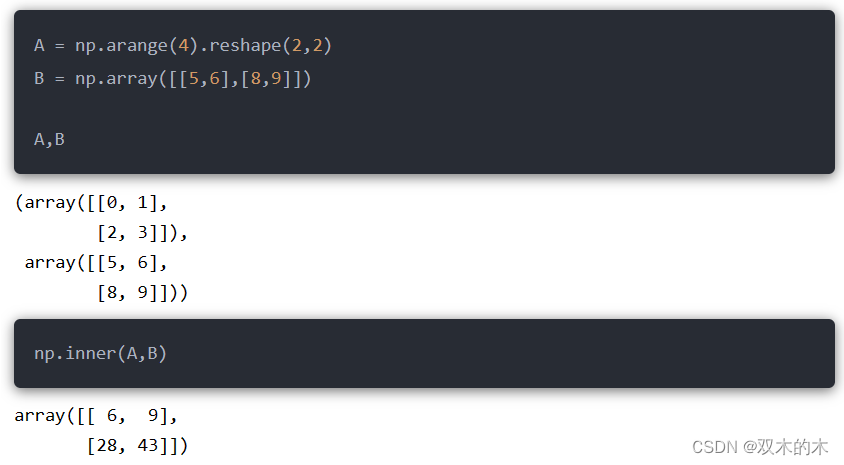
np.inner的计算过程是A中的每行元素乘以B中的每行元素再相加:
# 0*5+1*6 = 6 # 0*8+1*9 = 9 # 2*5+3*6 = 28 # 2*8+3*9 = 43
A中的每行元素乘以B中每列的元素:

15.4 np.matmul
两个矩阵的乘积;矩阵的维度必须相匹配。
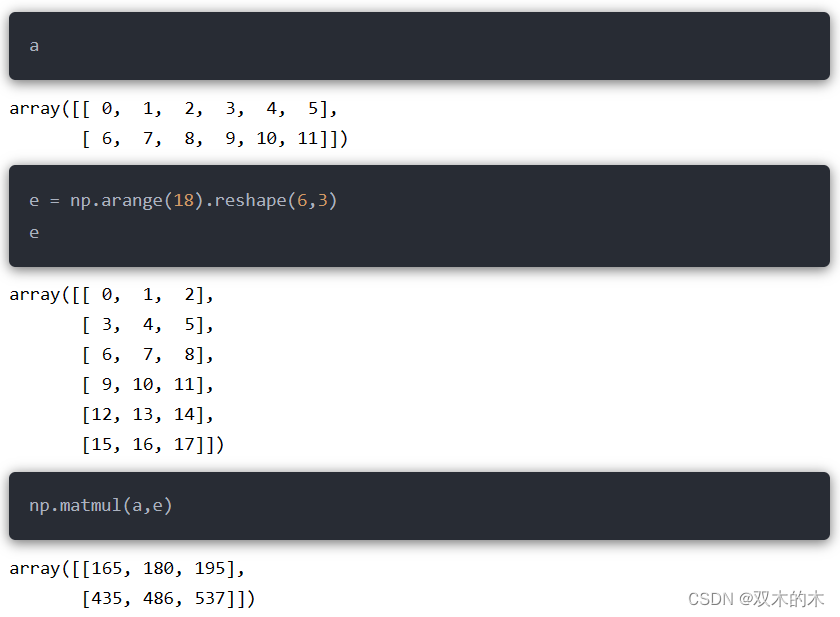
a是2*6,e是6*3,所以矩阵乘积的结果是2*3
15.5 np.linalg.det()
计算矩阵的行列式

15.6 np.linalg.solve()
计算线性矩阵方程组,并以矩阵的形式表示方程的解。
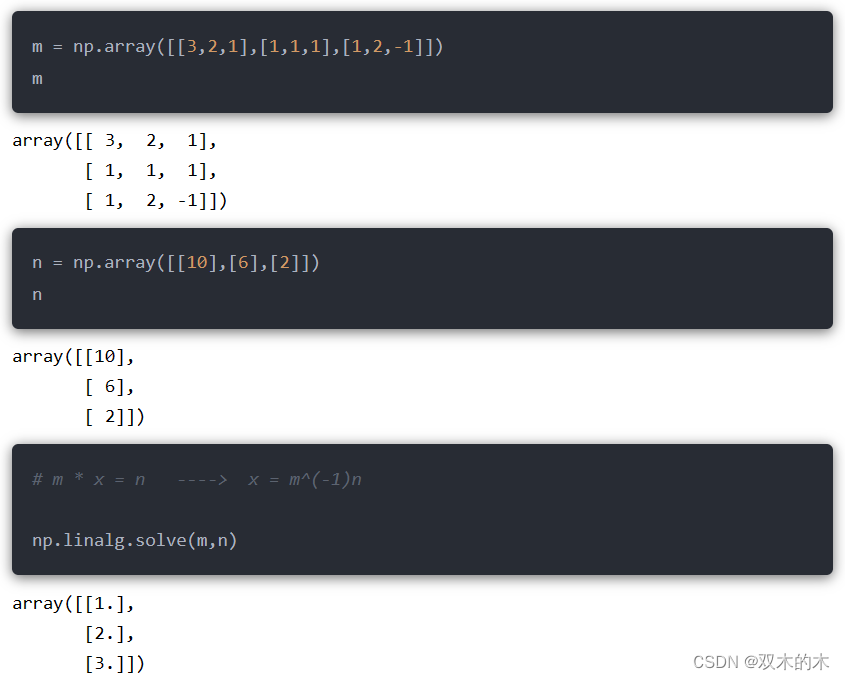
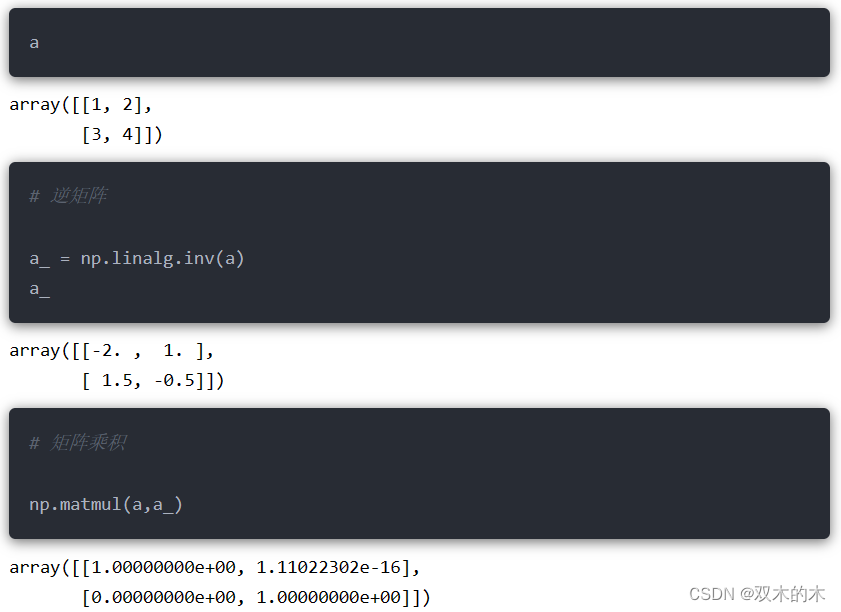
15.7 np.linalg.inv()
求解矩阵的逆矩阵;原矩阵和逆矩阵的矩阵乘积就是单位矩阵:
THE END!
文章结束,感谢阅读。大家有推荐的公众号可以评论区留言,共同学习,一起进步。







 本文详细介绍了Numpy的基本概念、数据类型、安装方法,以及从数组创建、索引切片、广播机制到数学运算、矩阵运算的全面指南,适合初学者快速上手。
本文详细介绍了Numpy的基本概念、数据类型、安装方法,以及从数组创建、索引切片、广播机制到数学运算、矩阵运算的全面指南,适合初学者快速上手。
















 409
409

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








