点击率预估模型01-FM因子分解机理论与实践

简介

因子分解机将支持向量机SVM的优势结合分解模型。如SVM，因子分解机是一个通用的预测器，可以用在任意实数值向量上。但是不同于SVM，因子分解机能通过分解参数对变量之间的交互关系进行建模；即使在非常稀疏的场景下，如推荐系统，也能对交叉特征进行建模。因子分解机可以通过算式优化，在线性时间内进行应用计算；而且不同于SVM在对偶形式中求解问题，FM在原问题空间进行求解，不需要支持向量等，可以直接对模型参数进行估计。

因子分解机FM模型

因子分解机FM的优势

• 在数据稀疏场景下仍然能进行参数预估；而SVM则不行；
• FM计算时间复杂度为线性时间，可以直接在原问题中进行优化，而且不依赖如支持向量机的支持向量。
• FM是一个通用预测器，可以用在任意的实值向量上。

模型

对于度为2的因子分解机模型FM：

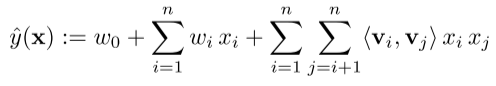
其中,表示长度为k的向量之间的內积。

矩阵V中的第i行向量$v_i$表示第i个变量的参数，其向量长度为k。

度为2的因子分解机能够捕获所有的单个变量和交叉变量：

• w0是全局偏置
• wi建模第i个变量的贡献
• ${\hat{w}}_{i,j}$表示第i个、第j个变量之间的交叉项。FM并不是直接用参数wij进行建模，而是通过分解，将其表示成两个向量的內积形式。其原因在于，对于稀疏数据，样本向量x中绝大部分元素均为0，进而导致建模特征i，j的变量wij也为0，通常情况下wij的估计，需要样本中存在xixj，即xi、xj均不为0；FM通过分解，由wiwj的內积来表示wij，所有和xi产生交叉的特征样本都可以用于估计wi，大大增加了模型的泛化性能。

因子分解机求解

因子分解机作为一个通用的预测器，可以用于：

• 分类问题：$\hat{y}(x)$的正负号当作分类结果。loss函数可以使用logit loss或hinge loss。
• 回归问题：$\hat{y}(x)$当作最终结果。loss可以使用均方根误差rmse。
• 排序问题：把$\hat{y}(x)$当作x的得分，对x进行排序。使用pair-wise loss。

因子分解机的公式可以表示成：线性回归+二阶交叉项。其求解过程主要集中在交叉项的计算。这项计算借鉴了完全平方公式：***(a+b)²=a²+2ab+b²***，2ab=(a+b)²-a²-b²

时间复杂度也从$O(k{n}^2)$变为了$O(kn)$。

参数的估计使用随机梯度下降法。

Code

github

Reference

jupyter版本

[简单易学的机器学习算法——因子分解机(Factorization Machine)])https://blog.youkuaiyun.com/google19890102/article/details/45532745)

---