高中数学-均值不等式

均值不等式（基本不等式）

两个正实数的几何平均数小于等于它们的算术平均数。公式a+b2≥ab。

【例】已知a>2,b>2，则a2b-2+b2a-2的最小值为（  ）

         A.2  B.4  C.6  D.16

【例】设a>b>0，则ab+4b2+1ba-b的最小值是（ D ）

A.2  B.3  C.4  D.6

解：b2+4b2+ab-b2+1ba-b=b2+4b2+ba-b+1ba-b≥24+21=6

【例】已知正数x，y满足x+2y=3，则xyx+8y的最大值为      。

【例】已知a>0,b>0，则a2+b2ab的最小值为  2    。

【例】已知x>0,y>0，且x+y+1x+1y=5，则x+y的最大值是（ B ）

A.3  B.4  C.6  D.8

21a+1b≤ab≤a-blna-lnb≤a+b2≤a2+b22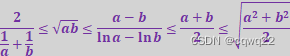

调和平均数≤几何平均数≤对数平均数≤代数平均数≤平方平均数

解：1x+1y=5-x+y，21x+1y≤x+y2，5-x+y=1x+1y≥4x+y，令x+y=t，

t2-5t+4≤0解出1≤t≤4

【2018成都二模】若直线xm+yn=2，(m,n>0)经过点3,1，则3m+n的最小值为(   )

A.16  B.8  C.12  D.14

已知ax+by=e，求cx+dy的最小值；已知cx+dy=e，求ax+by的最小值:ac+bd+2abcde

【例】已知a+2b=1，则2a+1b的最小值  8 

解：2+2+22*21=8

【2017山东】若直线xa+yb=1，(a,b>0)过点1,2，则2a+b的最小值  8 

【2016丽水模拟】已知a，b均为正数，且a+b=1，则4a+9b最小值为(  B  )

A.24  B.25  C.26  D.27