机器学习笔记(四）PCA主成分分析

首先先复习一下要用到的基础的知识：

（一）、协方差和方差

样本均值：

样本方差：

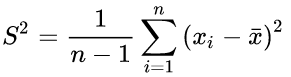
样本X和样本Y的协方差：

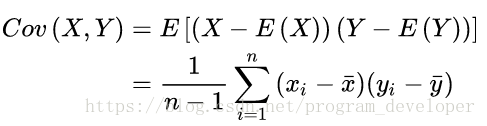
协方差代表了两个变量之间的相关关系，协方差为正时，说明X和Y是正相关关系；协方差为负时，说明X和Y是负相关关系；协方差为0时，说明X和Y是相互独立。Cov(X,X)就是X的方差。当样本是n维数据时，它们的协方差实际上是协方差矩阵(对称方阵)。例如，对于3维数据(x,y,z)，计算它的协方差就是：

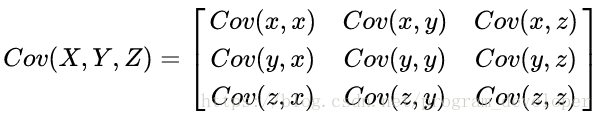
（二）、特征值与特征向量

如果向量v与变换A满足Ax=λx，则称向量x是变换A的一个特征向量，λ是相应的特征值。

描述正方形矩阵的特征值的重要工具是特征多项式，λ是A的特征值等价于线性方程组(A – λI) x = 0 （其中I是单位矩阵）有非零解x (一个特征向量)，因此等价于行列式|A – λI|=0  。

函数p(λ) = det(A – λI)是λ的多项式，因为行列式定义为一些乘积的和，这就是A的特征多项式。矩阵的特征值也就是其特征多项式的零点。一个矩阵A的特征值可以通过求解方程pA(λ) = 0来得到。 若A是一个n×n矩阵，则pA为n次多项式，因而A最多有n个特征值,包括虚数。但是如果是是对称矩阵的话他的特征值都是实数。Ax表示对向量x的旋转拉伸。如果Ax和x的方向一样，只是长度不一样，说明x是A的特征向量，拉伸倍数为λ。例如下图，x3是A的特征向量。

如果