hdu2845--beans

最新推荐文章于 2024-07-19 11:00:00 发布

原创最新推荐文章于 2024-07-19 11:00:00 发布 · 272 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划

杭电OJ 同时被 2 个专栏收录

21 篇文章

订阅专栏

动态规划

17 篇文章

订阅专栏

本文介绍了一种利用动态规划解决特定游戏问题的方法，该游戏要求玩家在一个矩阵中吃豆子并收集分数，但受特定规则限制。文章详细解释了如何通过动态规划算法找到在遵循游戏规则的情况下能获得的最大分数。

Problem Description
Bean-eating is an interesting game, everyone owns an MN matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 11 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.
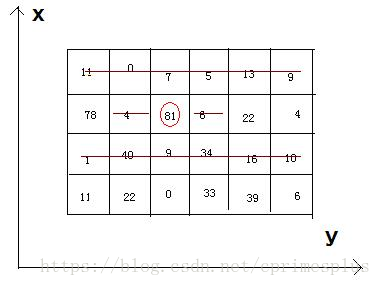
在这里插入图片描述

Now, how much qualities can you eat and then get ?

Input
There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn’t beyond 1000, and 1<=M*N<=200000.

Output
For each case, you just output the MAX qualities you can eat and then get.

分析：
这道题的解题方法：
dpx[i]----表示前i行的最大值
dpy[i]----表示当前行前i列元素和的最大值
那么对于dpx[i]来说，讨论最大值分为两种情况：(1)不加这一行，最大值为前一行结尾的最大值
(2)加入这一行，最大值为前两行结尾的最大值加上这一行的最大值
而通过分析发现：行的最大值和列的最大值求法同理。
即：
dpx[i]=max(dp[i-1],dp[i-2]+dpy[m+1])
dpy[j]=max(dp[j-1],dp[j-2]+num)
因为坐标涉及到i-2，因此我们令下表为2为第一行，那么循环就应该是从2到n+1为止。
代码：

//hdu2845beans
#include<stdio.h>
#include<string.h>
#define MAXN 200005
#define max(a,b) (a>b?a:b)
int main()
{
	int dpx[MAXN],dpy[MAXN];
	int i,j,k,num,m,n;
	while(~scanf("%d%d",&n,&m))
	{
		for(i=2;i<=n+1;i++)
		{
			for(j=2;j<=m+1;j++)
			{
				scanf("%d",&num);
				dpx[j]=max(dpx[j-1],dpx[j-2]+num);
			}
			dpy[i]=max(dpy[i-1],dpy[i-2]+dpx[m+1]);
		}
		printf("%d\n",dpy[n+1]);
	}
	return 0;
}

这道题给我的启发：整体规划，分开求解。