整数在内存中的储存
整数在2进制中有三种表示方法,分别是原码、反码和补码。
而对于有符号的整数,三种方法均有符号位和数值位两部分,符号位0表示正,0表示负,最高的一位为符号位,其余都是数值位。
正数的原码、反码、补码都相同
负数的三种方式各不相同
原码:直接按正负形式翻译成二进制形式
反码:符号位不变,其余位取反,把1变成0,把0变成1
补码:符号位不变,在反码的基础上加1
而整数在计算机中是以补码的形式储存的
大小端和字节序判断
什么是大小端
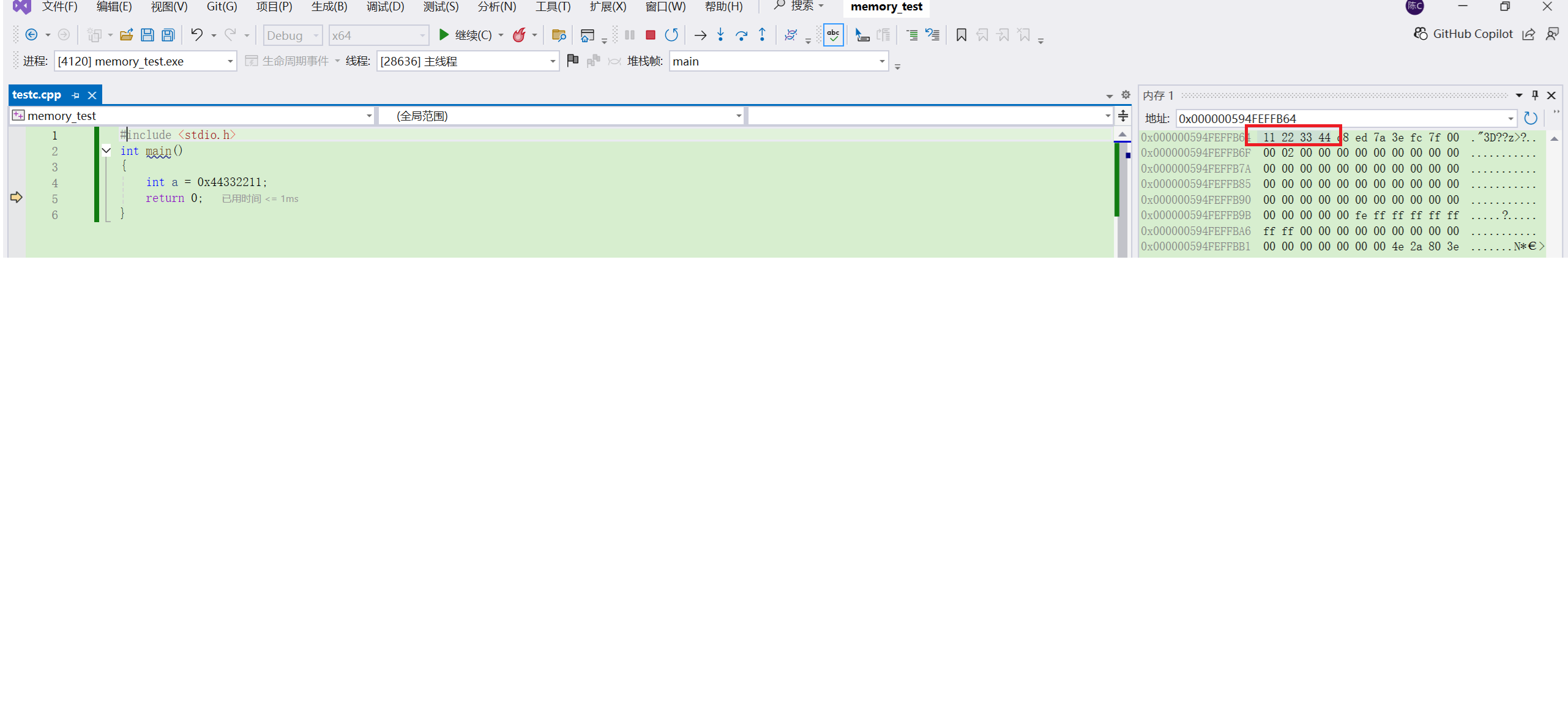
图中可知a为44332211(16进制),但在内存中却是倒着储存的,这是怎么回事呢?
当数据的字节位超过一个字节时,高低字节位的储存顺序的问题就会出现。就拿整型0x44332211举例,44是高位,11是地位,那么在地址由小到大的内存中是以44332211的形式储存呢,还是以11223344的形式储存呢?所以大小端的储存方式就出现了。
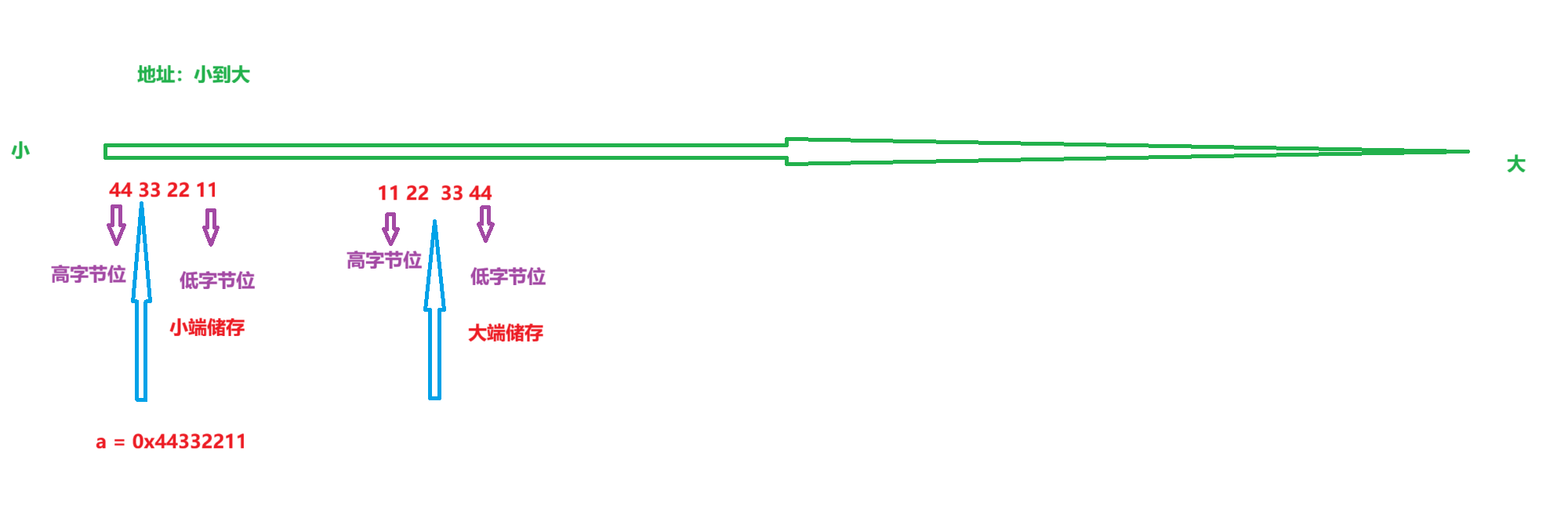
大端(存储)模式:
是指数据的低位字节内容保存在内存的⾼地址处,⽽数据的⾼位字节内容,保存内存的低地址处。
小端(存储)模式:
是指数据的低位字节内容保存在内存的低地址处,⽽数据的⾼位字节内容,保存在内存的⾼地址处
在不同的编译器中,是大端还是小端是不确定的。例如上图中VS2022就采用的是大端储存模式。
练习
练习1:
请简述⼤端字节序和⼩端字节序的概念,设计⼀个⼩程序来判断当前机器的字节序。(10分)-百度笔试题
概念上面已经说过了,下面我们来设计一下这个程序。
我们可以设一个整型a=0x10000000,然后用char*指针对a的第一个字节进行解引用,如果是1,就是小端;如果是0,就是大端。
#include <stdio.h>
int check_store(int a)
{
char*p = (char*) & a;
return *p;
}
int main()
{
int a = 0x10000000;
int ret = check_store(a);
if (ret == 1)
{
printf("小端");
}
else
{
printf("大端");
}
return 0;
}
当然,check_store也可以这样写:
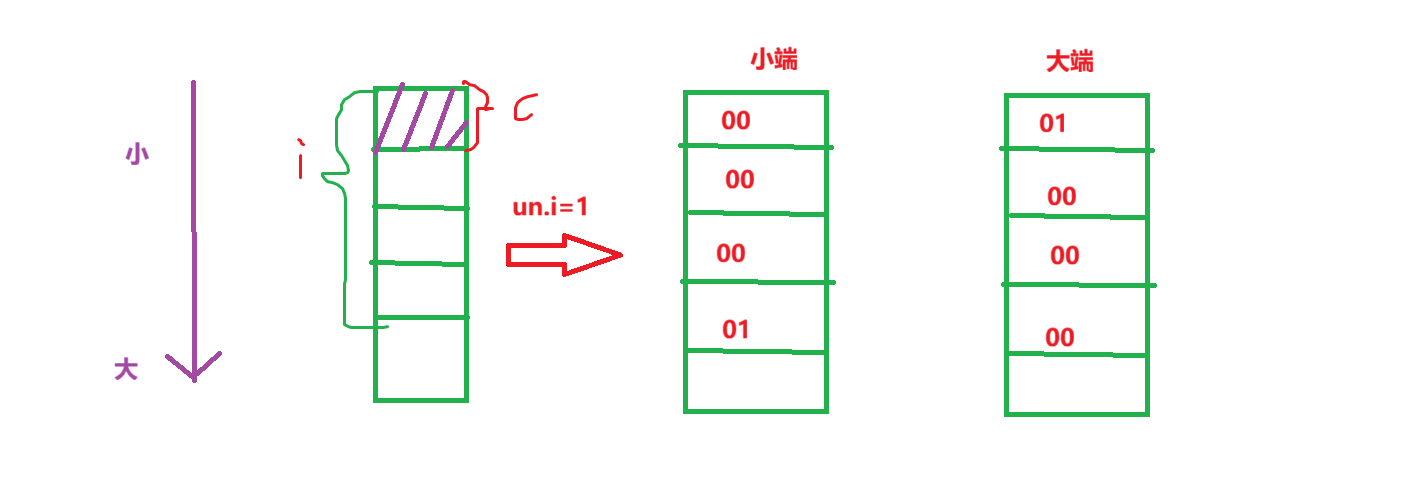
check_store()
{
union
{
int i;
char c;
}un;
un.i = 1;
return un.c;
}
由于联合体只为最大的成员分配足够多的空间,且所有成员共用一块内存空间,所以char c和int i共用第一个字节,i=1后,小端模式c = 0,大端模式c = 1。
练习2:
int main()
{
char a= -1;
signed char b=-1;
unsigned char c=-1;
printf("a=%d,b=%d,c=%d",a,b,c);
return 0;
}
请写出输出结果
这题考察我们char类型的储存范围和整型在内存中的储存
signed char类型的范围是-128~127,而unsigned char的范围是0~255,为什么是这样呢?

上面是signed char类型,而unsigned char便是正常的0~255了。
char是signed还是unsigned取决于编译器,而在vs中char是signed类型,所以输出a =-1,b=-1。
但是把-1赋给c时就不行了,-1的在内存储存是补码形式,即
11111111 11111111 11111111 11111111 //-1
但char只要后8位即
11111111
而c是unsigned类型,是正数,其补码就是原码,所以11111111就按正数形式读取,所以c=255。
验证一下:

练习3
题目1
#include <stdio.h>
int main
{
char a = -128;
printf("%u\n",a);
return 0;
}
题目2
#include <stdio.h>
int main()
{
char a = 128;
printf("%u\n",a);
return 0;
}
对于题目1,-128以原码形式存入char a中为10000000,将其以unsigned int形式提取时要进行整型提升,10000000变为11111111 11111111 11111111 10000000,即4294967168
整型提升的规则是
有符号的:整型提升时是按照变量的补码被截断时的最高位是什么进行补位的,如果截断后最高位即最左面的一位数为 1 则在最高位前补 1 ,如果最高位是 0 则在前面补 0 ,补够32位即int类型即可。无符号的 直接在被截断的前面补 0 即可。
对于题目2,char类型的范围是-128~127,而128超出了这个范围,128的补码是10000000,放在char里即为有符号整型,再进行整型提升变为11111111 11111111 11111111 10000000,依然是4294967168。
我们来试验一下:
练习4
#include <stdio.h>
int main()
{
char a[1000];
int i;
for(i=0; i<1000; i++)
{
a[i] = -1-i;
}
printf("%d",strlen(a));
return 0;
}
从表面上来看,-1-i依此为-1,-2,-3,…,-998,-999,-1000,但我们知道char是-128~127,所以事情并非这么简单
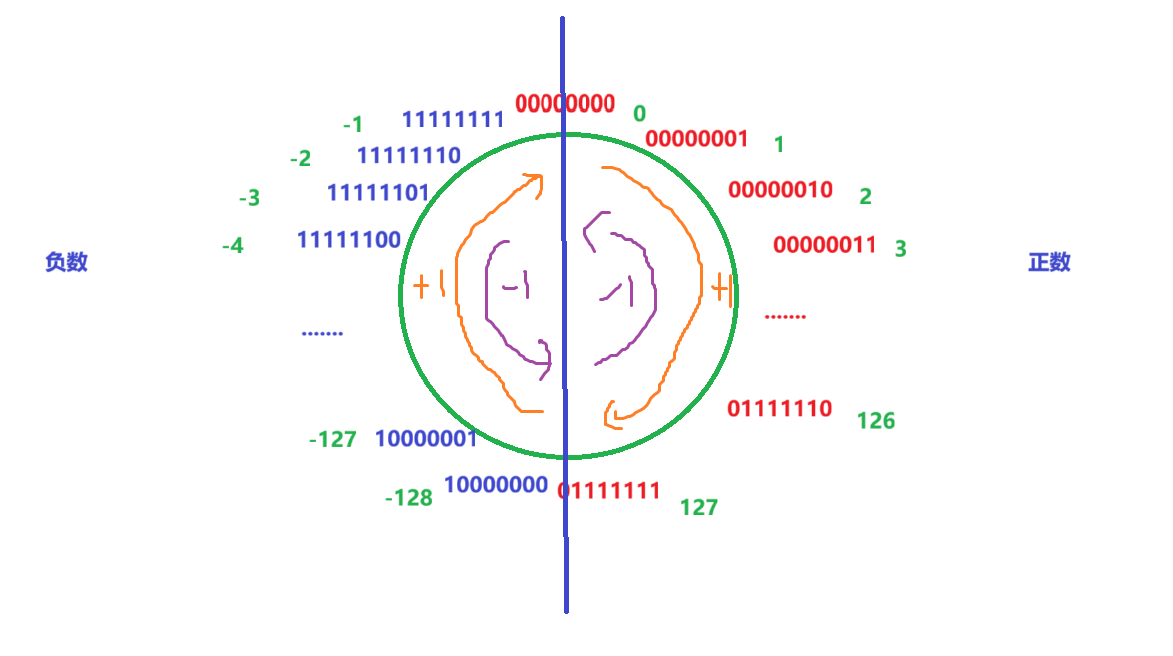
实际上当减到-128,11111111就会变成01111111,即127,然后126,125,124…
而strlen是统计‘/0’之前的字符个数,即char=0时停止统计,-1到-128为128个字符,127~1为127个字符,共255个,所以结果是255,验证一下:

浮点数在内存中的储存
练习
#include <stdio.h>
int main()
{
int n = 9;
float *pFloat = (float *)&n;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
*pFloat = 9.0;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
return 0;
}
输出什么
浮点数的储存

对于32位的浮点数(float),最⾼的1位存储符号位S,接着的8位存储指数E,剩下的23位存储有效数字。
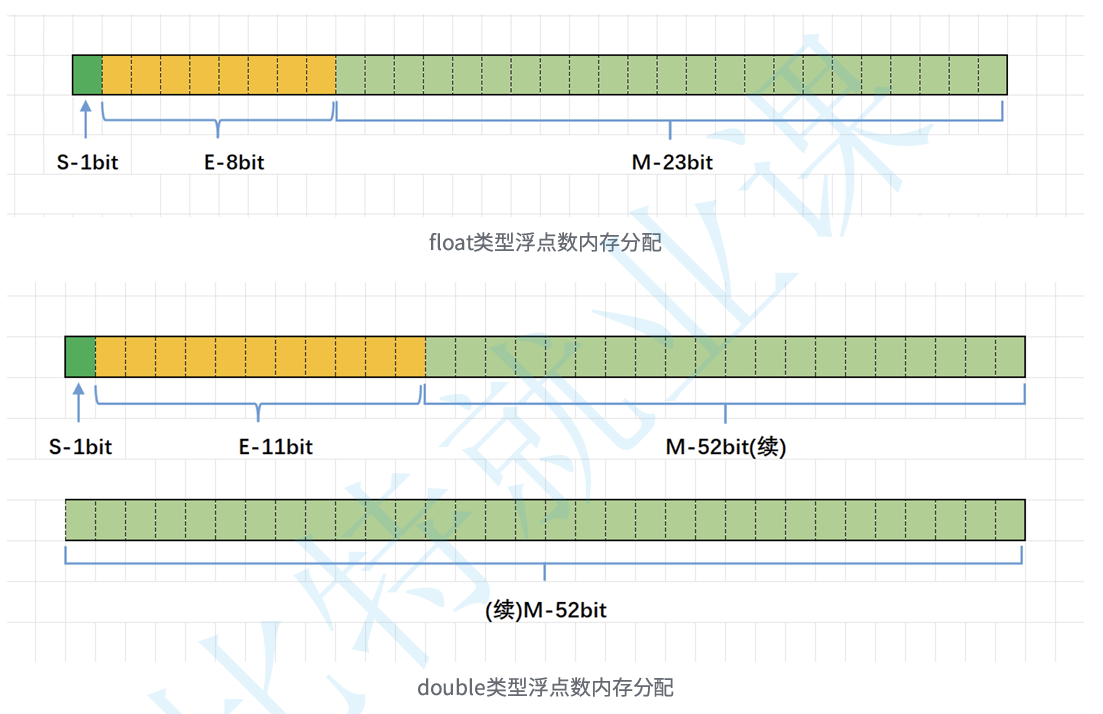
浮点数存的过程
IEEE 754对有效数字M和指数E,还有⼀些特别规定。
前⾯说过,1≤M<2 ,也就是说,M可以写成1.xxxxxx 的形式,其中xxxxxx 表⽰⼩数部分。
IEEE 754规定,在计算机内部保存M时,默认这个数的第⼀位总是1,因此可以被舍去,只保存后⾯的xxxxxx部分。⽐如保存1.01的时候,只保存01,等到读取的时候,再把第⼀位的1加上去。
浮点数取的过程
E不全为0或不全为1(常规情况)
这时,浮点数就采⽤下⾯的规则表⽰,即指数E的计算值减去127(或1023),得到真实值,再将有效
数字M前加上第⼀位的1。
E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值,有效数字M不再加上第⼀位的1,⽽是还原为0.xxxxxx的⼩数。这样做是为了表⽰±0,以及接近于0的很⼩的数字。
E全为1
这时,如果有效数字M全为0,表⽰±⽆穷⼤(正负取决于符号位s)。




















 2170
2170

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








